Les diagrammes en arbre sont très utiles en probabilités. On en distingue 2 sortes : les diagrammes qui permettent de représenter et de dénombrer toutes les possibilités de l’univers des possibles ainsi que ceux qui permettent de représenter et de calculer les probabilités de chacun des résultats.
Le diagramme en arbre, aussi appelé arbre de dénombrement ou arbre des possibilités, est une représentation visuelle qui permet de dénombrer tous les résultats possibles d’une expérience aléatoire à plusieurs étapes.
On lance successivement une pièce de monnaie et un dé à |6| faces. Combien y a-t-il de résultats possibles?
On commence par le 1er lancer, soit celui de la pièce de monnaie. Les cas possibles sont pile (P) ou face (F). On trace donc |2| branches comme ceci.
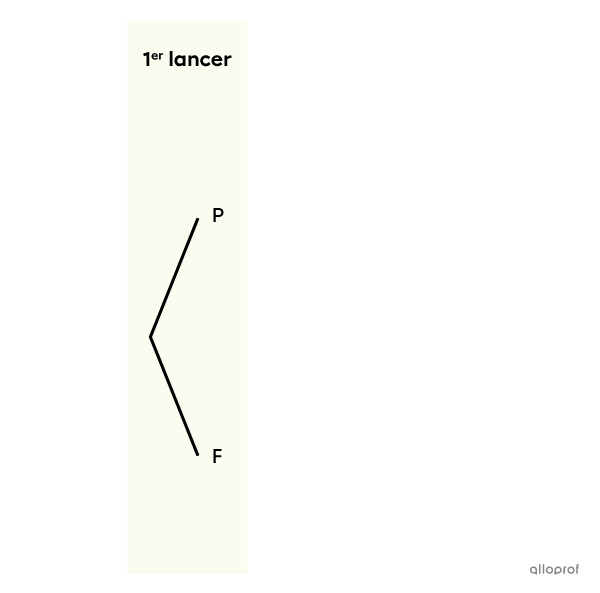
On continue avec le 2e lancer, soit celui du dé. Les cas possibles pour le lancer d’un dé à |6| faces sont : 1, 2, 3, 4, 5 et 6. On trace donc |6| branches au bout de chacune des 2 branches du 1er lancer. Pour compléter, on note les résultats possibles entre parenthèses dans une colonne située à droite.

En comptant les résultats possibles un par un, on en dénombre |12.| On peut aussi utiliser le principe de multiplication étant donné que chacune des |2| branches du premier lancer a généré |6| branches. Il y a donc |2\times 6=12| possibilités.
Le diagramme en arbre ne doit pas partir dans tous les sens. Les résultats de chaque étape de l’expérience aléatoire doivent tous être alignés verticalement (dans une même colonne entièrement à droite de l’étape précédente). Au besoin, on ajoute la colonne Résultats complètement à droite.

Si l’expérience aléatoire est composée d’évènements élémentaires qui sont équiprobables, alors, après avoir dénombré tous les résultats possibles à l’aide d’un diagramme en arbre, on peut répondre à des questions de probabilités.
Quelle est la probabilité d’obtenir pile au moins 2 fois de suite si tu lances 3 pièces de monnaie successivement?
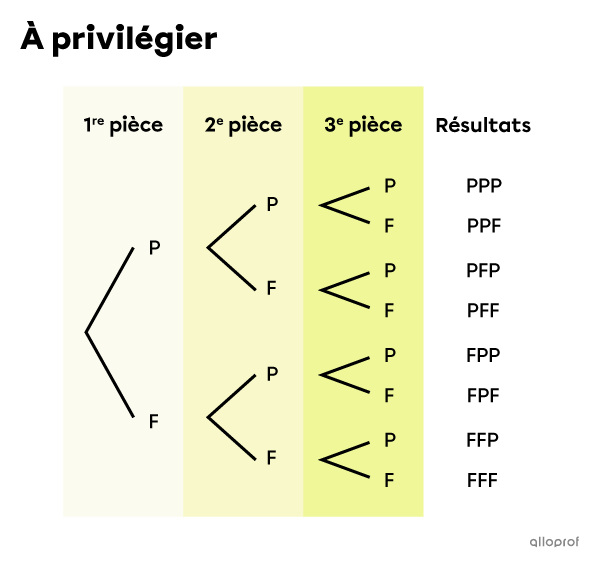
On commence par faire le diagramme en arbre où on va représenter le résultat pile par la lettre P et le résultat face par la lettre F.
Il s’agit d’une expérience aléatoire avec remise à 3 étapes où on tient compte de l’ordre, car on lance successivement 3 pièces de monnaie qui ont toutes un côté pile et un côté face.

On remarque qu’il y a 8 résultats possibles : PPP, PPF, PFP, PFF, FPP, FPF, FFP et FFF. Ces 8 cas sont tous équiprobables, car la probabilité théorique d’obtenir le côté pile est toujours égale à celle d’obtenir le côté face.
Parmi ces 8 cas, il y en a 3 qui présentent au moins 2 fois de suite le côté pile : PPP, PPF et FPP.
Comme il y a 3 cas favorables à l’évènement « obtenir pile au moins 2 fois de suite » et que tous les cas possibles sont équiprobables, on a la probabilité suivante.||\begin{align}P\left(\begin{gathered}\text{obtenir pile au moins}\\ \text{2 fois de suite}\end{gathered}\right)&=\dfrac{\text{Nombre de cas favorables}}{\text{Nombre de cas possibles}}\\ &=\dfrac{3}{8}\end{align}||Réponse : La probabilité d’obtenir au moins 2 fois de suite le côté pile est de |\dfrac{3}{8}.|
Dans un diagramme en arbre, on retrouve chaque résultat une seule fois, même si certains résultats ont une plus grande probabilité de se produire que d’autres. Par exemple, si on fait un tirage avec remise de 2 billes dans un sac qui contient 2 billes noires (N) et 1 bille blanche (B), on devrait obtenir le 1er diagramme ci-dessous, c’est-à-dire celui qui montre 4 résultats possibles.
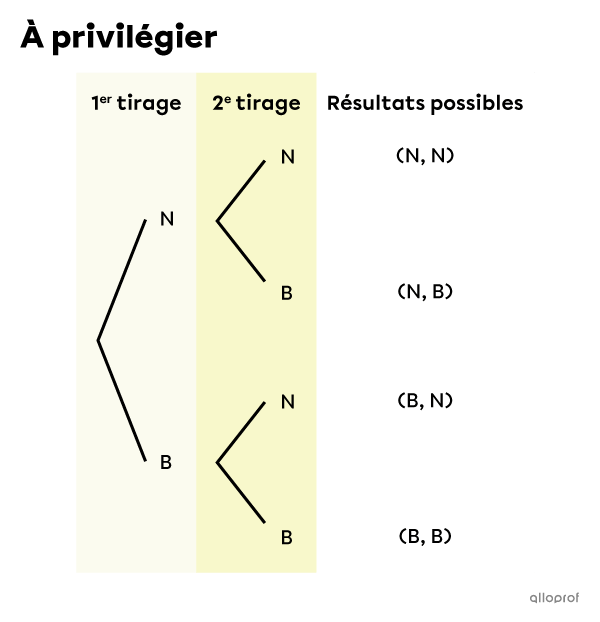
Il y a donc 4 résultats possibles, même s’ils ne sont pas tous équiprobables. Pour le moment, on ne peut donc pas répondre à des questions de probabilités à moins de transformer cet arbre de possibilités en arbre de probabilités.
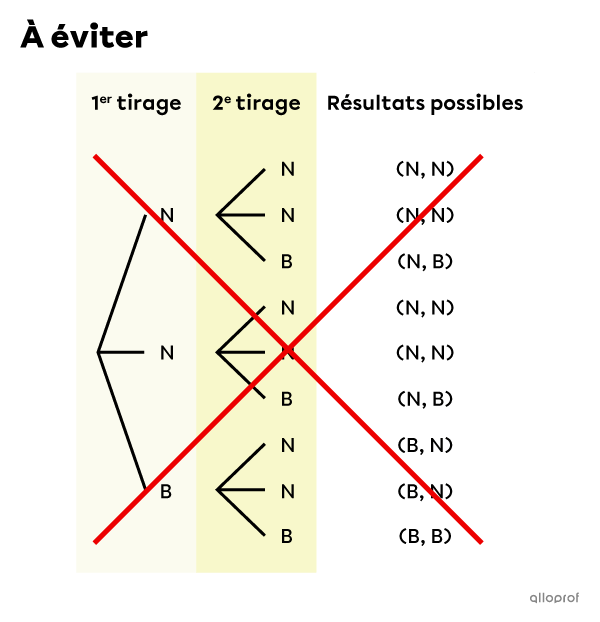
Ce diagramme porte à confusion, puisqu’on dirait qu’il y a 9 résultats possibles, mais il n’y en a que 4 différents. Autrement dit, on y a tracé des branches inutilement.
L’arbre des probabilités est un diagramme en arbre dans lequel on ajoute les probabilités de chaque branche d’une expérience aléatoire à plusieurs étapes.
Une erreur s’est glissée dans cette vidéo.
À 2 min 31 s, on devrait entendre « R, B » et non « R, V ».
Pour répondre à des questions de probabilités à l’aide d’un arbre de probabilités, on suit la démarche suivante.
-
Déterminer les résultats possibles.
-
Faire la liste des possibilités.
-
Placer les probabilités sur les branches.
-
Calculer la probabilité de chaque possibilité.
-
Calculer la probabilité que l’on cherche.
Il y a 2 situations possibles.
Dans le cas d'une expérience aléatoire avec remise, les probabilités à inscrire sur chacune des branches du diagramme sont les mêmes d’une étape à l’autre.
Romy découpe toutes les lettres du mot MISSISSIPPI et les place dans un sac. Elle tire une 1re lettre au hasard, la note, puis la remet dans le sac. Ensuite, elle tire une 2e lettre. Avec les 2 lettres pigées, elle forme un code de 2 lettres. Elle veut savoir quelle est la probabilité que son code soit formé de 2 lettres différentes.
-
Déterminer les résultats possibles
On commence par faire le diagramme en arbre de la situation pour dénombrer tous les résultats possibles.
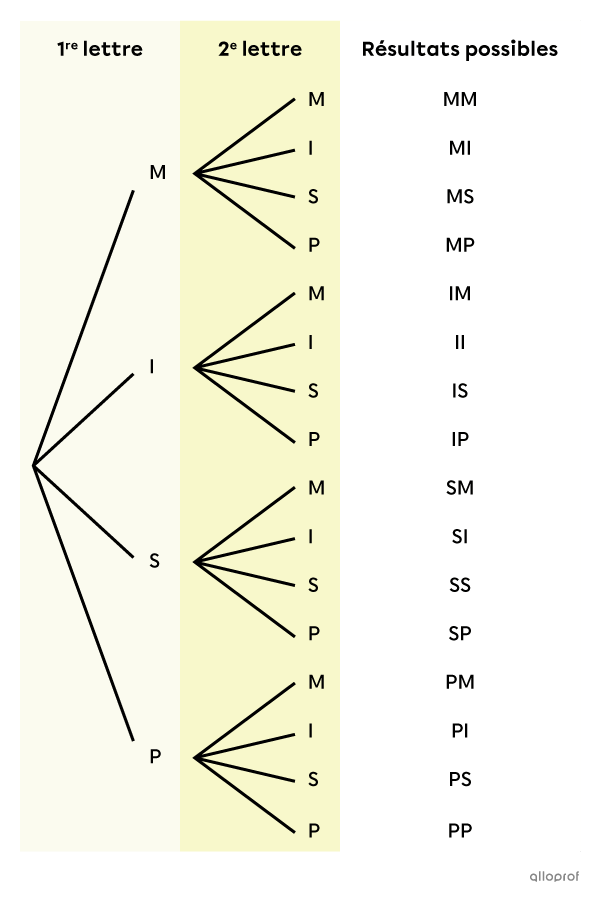
Il y a donc |4\times 4=16| résultats possibles.
-
Faire la liste des possibilités
Les possibilités sont les résultats finaux de l’expérience : MM, MI, MS, MP, IM, II, IS, IP, SM, SI, SS, SP, PM, PI, PS et PP. Dans l’arbre des possibilités, on les retrouve dans la colonne située complètement à droite. -
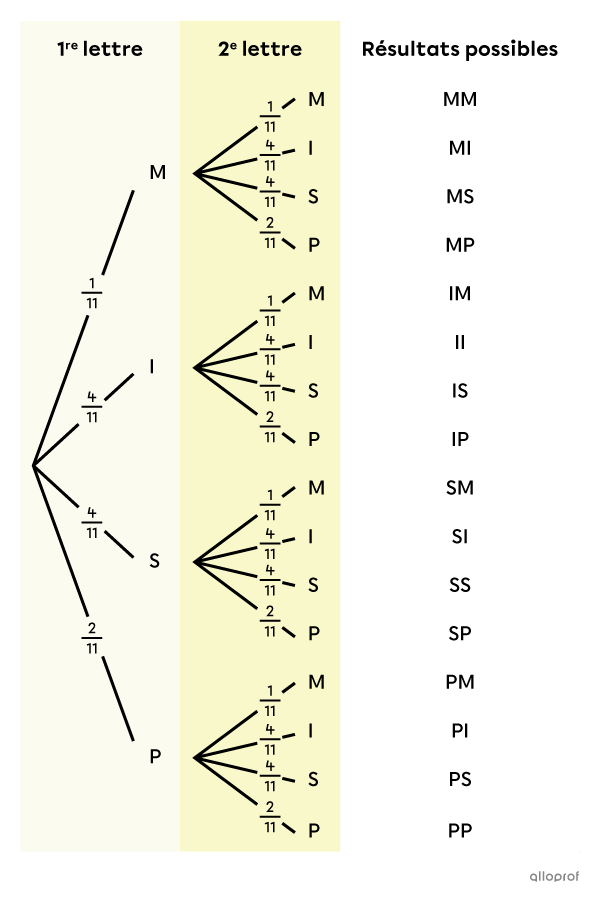
Placer les probabilités sur les branches
Dans l’arbre des probabilités suivant, les probabilités associées au 1er tirage sont les mêmes que celles associées au 2e tirage.
-
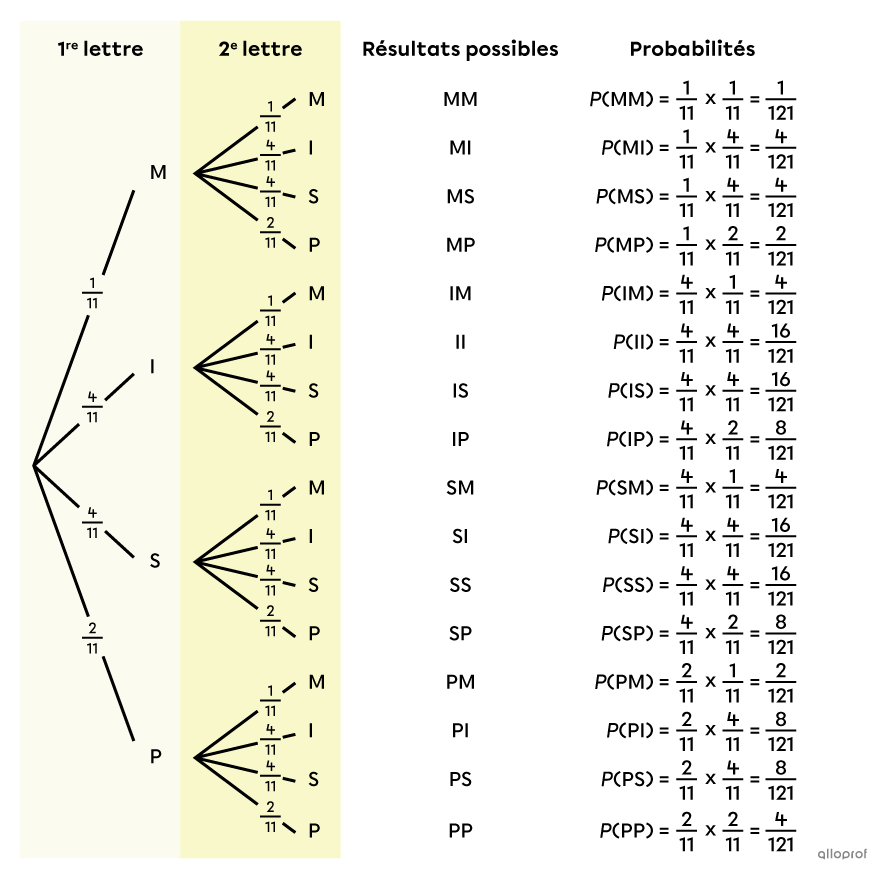
Calculer la probabilité de chaque possibilité
Pour calculer la probabilité de chaque résultat possible, on utilise le principe de multiplication : on calcule le produit des probabilités situées sur les branches qui nous amènent à ce résultat. Par exemple, pour MM, on fait |\dfrac{1}{11}\times \dfrac{1}{11},| pour MI, on fait |\dfrac{1}{11}\times \dfrac{4}{11},| etc. On obtient alors l’arbre des probabilités complet suivant.
-
Calculer la probabilité que l’on cherche
On se rappelle que Romy veut savoir la probabilité que son code soit formé de 2 lettres différentes. On peut y arriver en additionnant la probabilité de tous les cas favorables : MI, MS, MP, IM, IS, IP, SM, SI, SP, PM, PI et PS. ||\begin{align}P\left(\begin{gathered}\text{obtenir 2 lettres}\\ \text{différentes}\end{gathered}\right) =\ &P(\text{MI})+P(\text{MS})+P(\text{MP})+P(\text{IM})+P(\text{IS})+P(\text{IP})\,+\\&P(\text{SM})+P(\text{SI})+P(\text{SP})+P(\text{PM})+P(\text{PI})+P(\text{PS})\\ =\ &\dfrac{4}{121}+\dfrac{4}{121}+\dfrac{2}{121}+\dfrac{4}{121}+\dfrac{16}{121}+\dfrac{8}{121}+\\&\dfrac{4}{121}+\dfrac{16}{121}+\dfrac{8}{121}+\dfrac{2}{121}+\dfrac{8}{121}+\dfrac{8}{121}\\ =\ &\dfrac{84}{121}\end{align}||Réponse : La probabilité que le code de Romy soit formé de 2 lettres différentes est de |\dfrac{84}{121},| soit environ |69\ \%.|
Les évènements « obtenir un code formé de 2 lettres différentes » et « obtenir un code formé de 2 lettres identiques » sont des évènements complémentaires. Sachant que la somme des probabilités de 2 évènements complémentaires donne toujours |100\ \%,| il est parfois plus efficace de calculer la probabilité de l’évènement complémentaire à l’évènement recherché, puis d’effectuer une soustraction, que de calculer directement la probabilité demandée. Dans l’exemple précédent, le calcul final aurait été le suivant. ||\begin{align}P(\text{obtenir 2 lettres différentes})&=100\ \% -P(\text{obtenir 2 lettres identiques})\\ &=100\ \%-\big(P(\text{MM})+P(\text{II})+P(\text{SS}) + P(\text{PP})\big)\\&=\dfrac{121}{121}-\left(\dfrac{1}{121}+\dfrac{16}{121}+\dfrac{16}{121}+\dfrac{4}{121}\right)\\&=\dfrac{121}{121}-\dfrac{37}{121}\\&=\dfrac{84}{121}\end{align}||
Dans un arbre de probabilités, la somme des probabilités de chaque regroupement de branches doit toujours donner |1,| soit |100\ \%.|
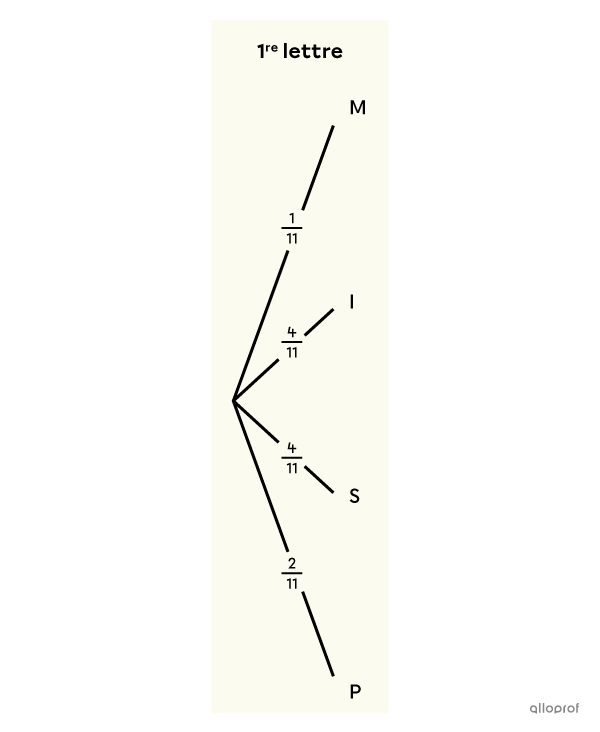
||\dfrac{1}{11}+\dfrac{4}{11}+\dfrac{4}{11}+\dfrac{2}{11}=\dfrac{11}{11}=1||La somme des probabilités des 4 branches donne bel et bien |100\ \%.| Si ce n’est pas le cas, c’est le signe qu’il y a une erreur à corriger.
La somme des probabilités de tous les résultats possibles de notre arbre doit aussi donner |100\ \%.|
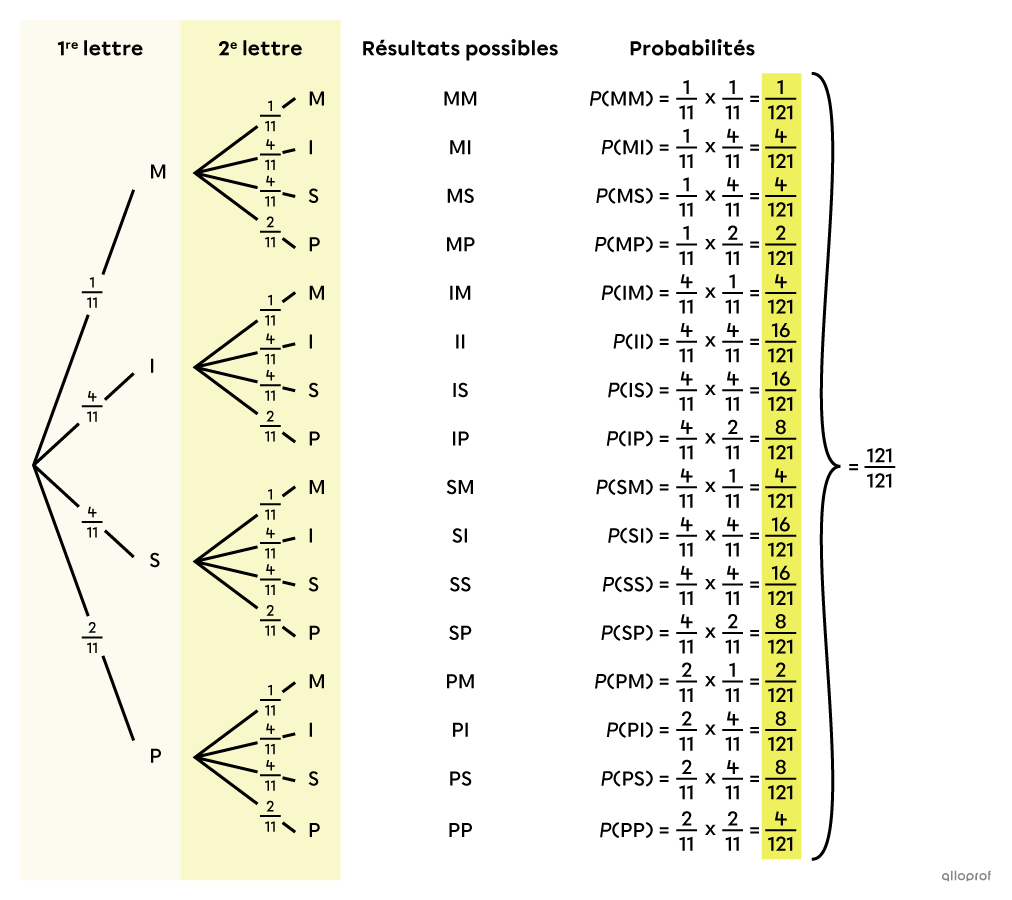
||\begin{align}\dfrac{1}{121}+\dfrac{4}{121}+\dfrac{4}{121}+\dfrac{2}{121}+\dfrac{4}{121}+\dfrac{16}{121}+\dfrac{16}{121}+\dfrac{8}{121}\,&+\\ \dfrac{4}{121}+\dfrac{16}{121}+\dfrac{16}{121}+\dfrac{8}{121}+\dfrac{2}{121}+\dfrac{8}{121}+\dfrac{8}{121}+\dfrac{4}{121}&=\dfrac{121}{121}\end{align}||La somme de toutes les probabilités donne bel et bien |100\ \%.| Si ce n’est pas le cas, c’est le signe qu’il y a une erreur à corriger.
Dans le cas d'une expérience aléatoire sans remise, les probabilités à inscrire sur chacune des branches du diagramme changent d’une étape à l’autre.
Romy découpe toutes les lettres du mot MISSISSIPPI et les place dans un sac. Ensuite, elle tire en même temps 2 lettres au hasard pour former un code de 2 lettres. Elle veut savoir quelle est la probabilité que son code soit formé de 2 lettres différentes.
-
Déterminer les résultats possibles
On commence par faire le diagramme en arbre de la situation pour représenter tous les résultats possibles. Comme on pige les 2 lettres en même temps, il s’agit d’une expérience aléatoire sans remise.
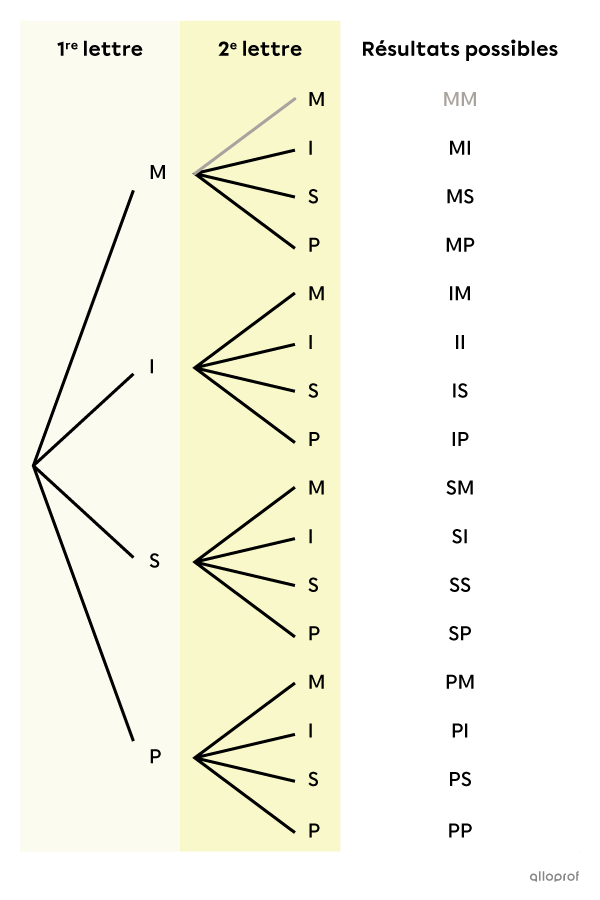
Il y a donc |15| résultats possibles, puisque le résultat MM est impossible. En effet, c’est un tirage sans remise et il n’y a qu’une lettre M dans le sac. On aurait donc pu décider de ne pas mettre du tout cette branche dans le diagramme.
-
Faire la liste des possibilités
Les résultats de l’univers des possibles sont : MI, MS, MP, IM, II, IS, IP, SM, SI, SS, SP, PM, PI, PS et PP.
-
Placer les probabilités sur les branches
On obtient l’arbre des probabilités suivant.
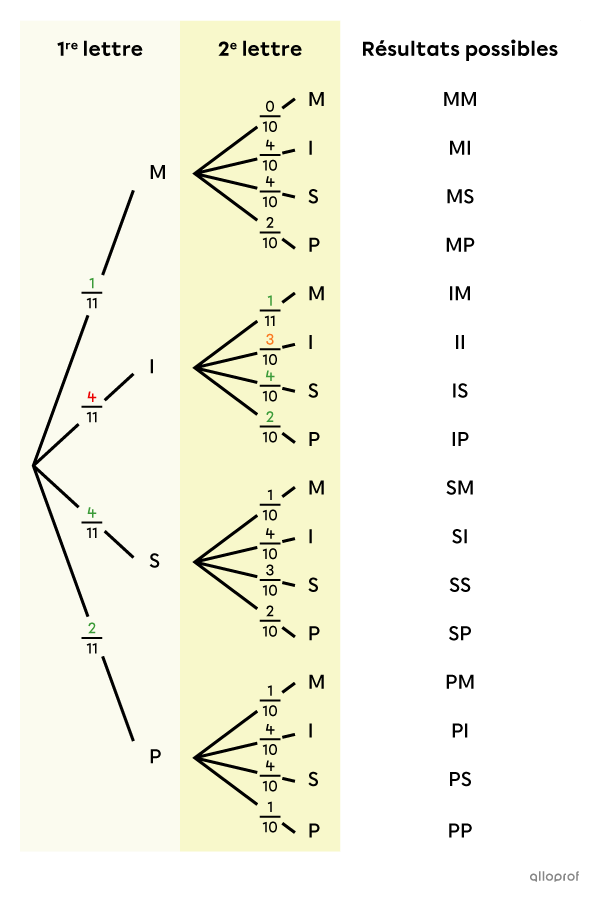
Les fractions associées au 1er tirage ont un dénominateur de 11, car il y a 11 lettres dans le sac lors du 1er tirage.
Les fractions au 2e tirage sont sur 10, car il ne reste que 10 lettres étant donné qu’on ne remet pas la lettre pigée dans le sac.
Les numérateurs ne changent pas sauf pour l’option sélectionnée au tirage précédent. Par exemple, si on pige une des 4 lettres I au 1er tirage, il ne reste que 3 lettres I pour le 2e tirage.
Remarques :
Pour le cas MM, la probabilité sur la 2e branche est de |\dfrac{0}{10},| car il ne reste plus de lettre M dans le sac.
Pour chaque regroupement de branches du 1er et du 2e tirage, la somme des probabilités donne toujours |1.| ||\begin{align}\dfrac{1}{11}+\dfrac{4}{11}+\dfrac{4}{11}+\dfrac{2}{11}&=\dfrac{11}{11}\\ \dfrac{0}{10}+\dfrac{4}{10}+\dfrac{4}{10}+\dfrac{2}{10}&=\dfrac{10}{10}\\ \dfrac{1}{10}+\dfrac{3}{10}+\dfrac{4}{10}+\dfrac{2}{10}&=\dfrac{10}{10} \\ \dots\end{align}||On peut donc aller de l’avant.
-
Calculer la probabilité de chaque possibilité
Pour calculer la probabilité de chaque résultat possible, on utilise le principe de multiplication : on calcule le produit des probabilités situées sur les 2 branches qui nous amènent à cette possibilité. Par exemple, pour MM, on fait |\dfrac{1}{11}\times \dfrac{0}{10},| pour MI, on fait |\dfrac{1}{11}\times \dfrac{4}{10},| etc.
On obtient l’arbre des probabilités complet suivant.
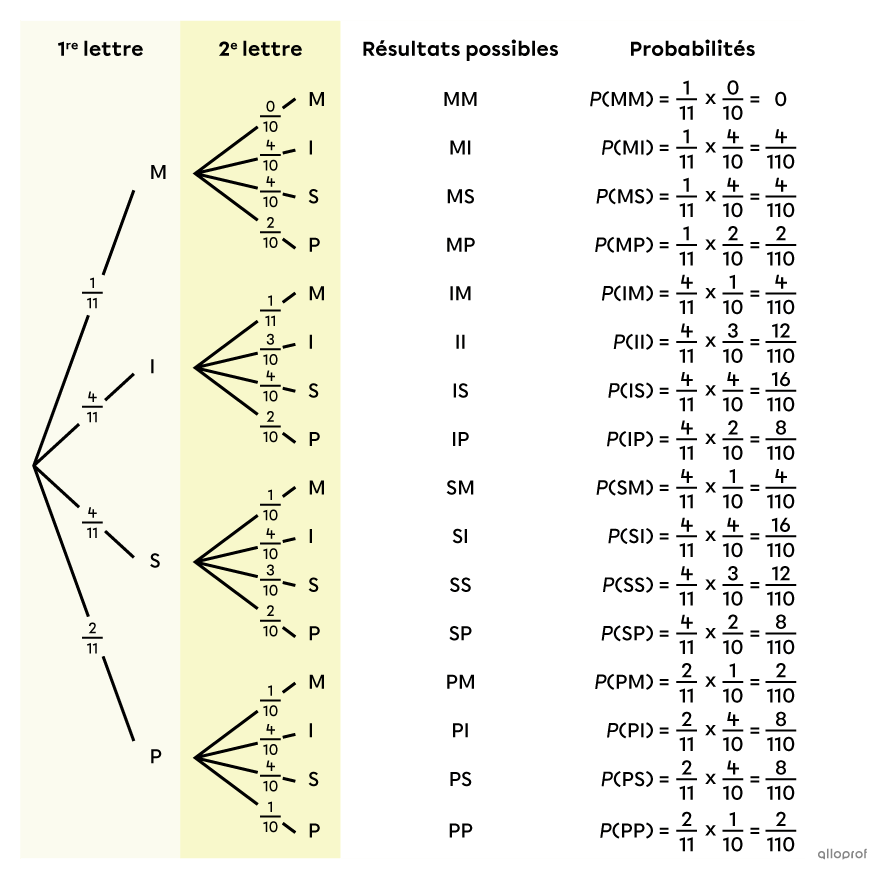
Remarque : Sur l’arbre des probabilités, les fractions auraient pu être réduites, mais comme il y a des additions de fractions à faire pour compléter le problème, il est plus pratique de ne pas les simplifier tout de suite.
-
Calculer la probabilité que l’on cherche
On se rappelle que Romy veut savoir la probabilité que son code soit formé de 2 lettres différentes. On peut y arriver en additionnant la probabilité de tous les cas favorables : MI, MS, MP, IM, IS, IP, SM, SI, SP, PM, PI et PS. On peut aussi faire |100\ \%| moins la probabilité d’avoir 2 lettres identiques. C’est ce qu’on fait pour avoir moins de calculs à effectuer. ||\begin{align}P(\text{obtenir 2 lettres différentes})&=100\ \% -\big(P(\text{MM})+P(\text{II})+P(\text{SS}) + P(\text{PP})\big)\\&=\dfrac{110}{110}-\left(\dfrac{0}{110}+\dfrac{12}{110}+\dfrac{12}{110}+\dfrac{2}{110}\right)\\&=\dfrac{110}{110}-\dfrac{26}{110}\\&=\dfrac{84}{110}\end{align}||Réponse : La probabilité que le code de Romy soit formé de 2 lettres différentes est de |\dfrac{84}{110},| soit environ |76\ \%.|
Les 2 derniers exemples sont des problèmes d’arrangement avec et sans remise.
On retrouve aussi des diagrammes en arbre dans d’autres branches des mathématiques.
-
En arithmétique, on utilise un arbre de facteurs pour déterminer la factorisation première d’un nombre.
-
Dans la théorie des graphes, un arbre est un graphe connexe sans cycle simple.