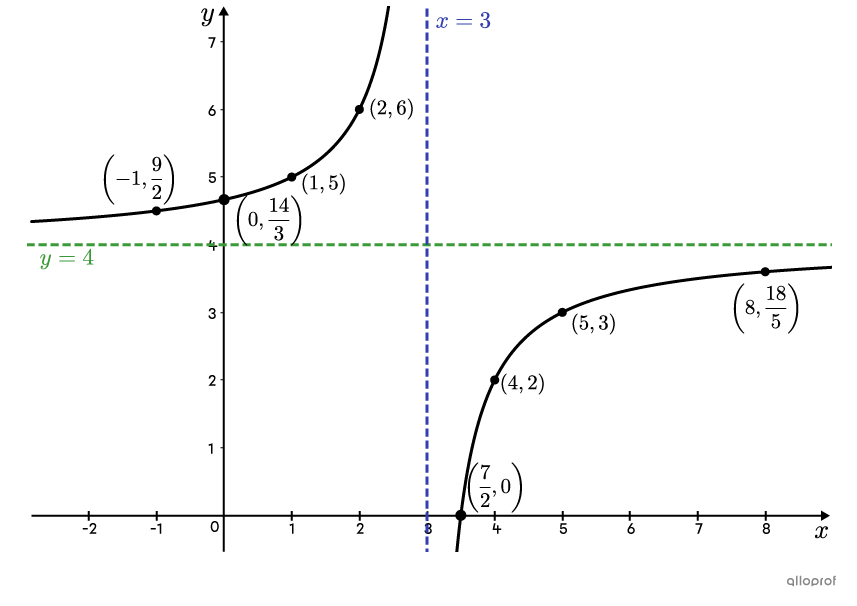Pour tracer le graphique d’une fonction rationnelle, il faut s’assurer que la règle de la fonction est écrite sous la forme canonique.
La règle d'une fonction rationnelle sous la forme canonique est |f(x)=\dfrac{a}{b(x-h)}+k.|
On peut faire rapidement une esquisse du graphique en observant les paramètres |a,| |b,| |h| et |k.|
-
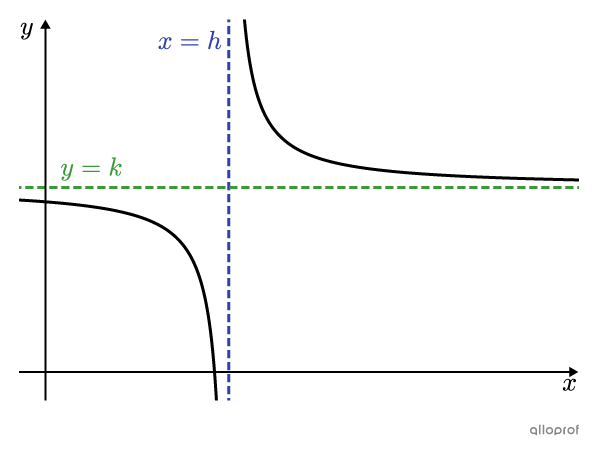
Le graphique d’une fonction rationnelle comprend 2 asymptotes :
Une asymptote verticale à |x=h;|
Une asymptote horizontale à |y=k.| -
L’emplacement des 2 branches de la fonction est dictée par le signe des paramètres |a| et |b.|
Si |a| et |b| sont de même signe |(ab>0),| alors les 2 courbes sont décroissantes. Elles sont ainsi situées en haut à droite et en bas à gauche des asymptotes.
Si |a| et |b| sont de signes contraires |(ab<0),| alors les 2 courbes sont croissantes. Elles sont ainsi situées en haut à gauche et en bas à droite des asymptotes.
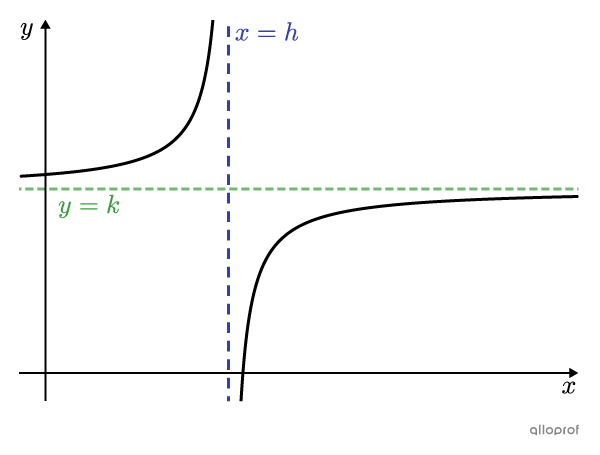
Remarque : La courbe d’une fonction rationnelle, formée de 2 branches, est une hyperbole.
La démarche à effectuer pour tracer précisément une fonction rationnelle dans un graphique est la suivante.
-
Trouver les équations des asymptotes en utilisant les paramètres |h| et |k.|
-
Trouver les coordonnées de quelques points.
-
Tracer les 2 asymptotes et situer les points trouvés dans le plan cartésien.
-
Tracer les 2 courbes qui passent par les points situés précédemment et qui se rapprochent des asymptotes sans y toucher.
Bien qu’ils n’existent pas toujours pour une fonction rationnelle, l’ordonnée à l’origine et le zéro de la fonction sont deux points remarquables qui sont intéressants à utiliser pour tracer un graphique.
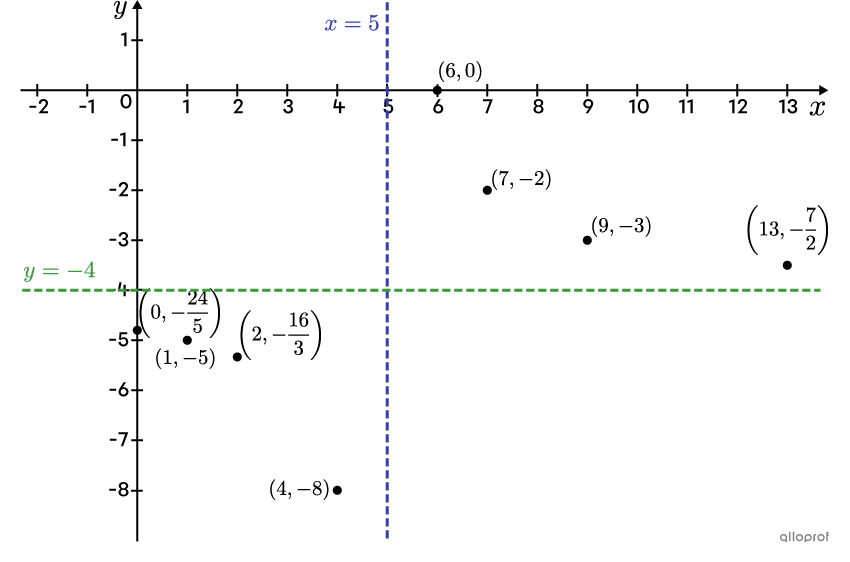
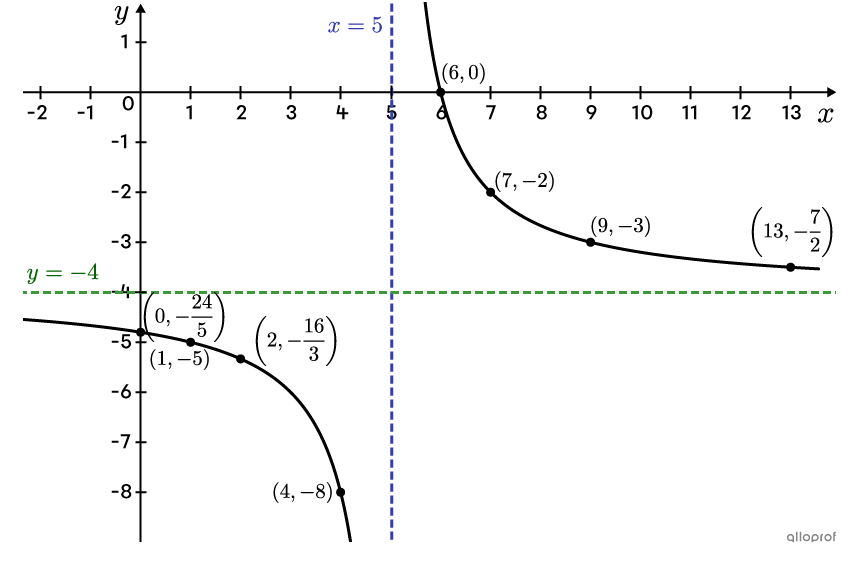
Trace la fonction rationnelle suivante. ||f(x)=\dfrac{8}{2(x-5)}-4||
-
Trouver les équations des asymptotes en utilisant les paramètres |h| et |k|
L'équation de l'asymptote verticale est donnée par |\color{#3b87cd}{x=h}|, donc |\color{#3b87cd}{x=5}.|
L'équation de l'asymptote horizontale est donnée par |\color{#3a9a38}{y=k}|, donc |\color{#3a9a38}{y=-4}.|
-
Trouver les coordonnées de quelques points
|
On remplace |x| par |0.| |
On remplace |x| par |1.| |
|---|---|
|
||\begin{align} |
||\begin{align} |
Avec cette démarche, on peut trouver d'autres couples.
|\left(2,-\dfrac{16}{3}\right),| |(4,-8),| |(7,-2),| |(9,-3),| |\left(13,-\dfrac{7}{2}\right)|
Si on veut aussi trouver le zéro de la fonction, on remplace |f(x)| par |0| et on isole |x.| ||\begin{align} \color{#560fa5}{f(x)}&=\dfrac{8}{2(x-5)}-4 \\
\color{#560fa5}{0}&=\dfrac{8}{2(x-5)}-4\\
\color{#ff55c3}{4}&=\dfrac{8}{\color{#ff55c3}{2(x-5)}} \\
\color{#ff55c3}{2(x-5)}&=\dfrac{8}{\color{#ff55c3}{4}} \\
2(x-5)&=2 \\x-5 &= 1\\x &=6 \end{align}||On obtient le couple |(6,0).|
-
Tracer les 2 asymptotes et situer les points trouvés dans le plan cartésien
-
Tracer les 2 courbes qui passent par les points situés précédemment et qui se rapprochent des asymptotes sans y toucher
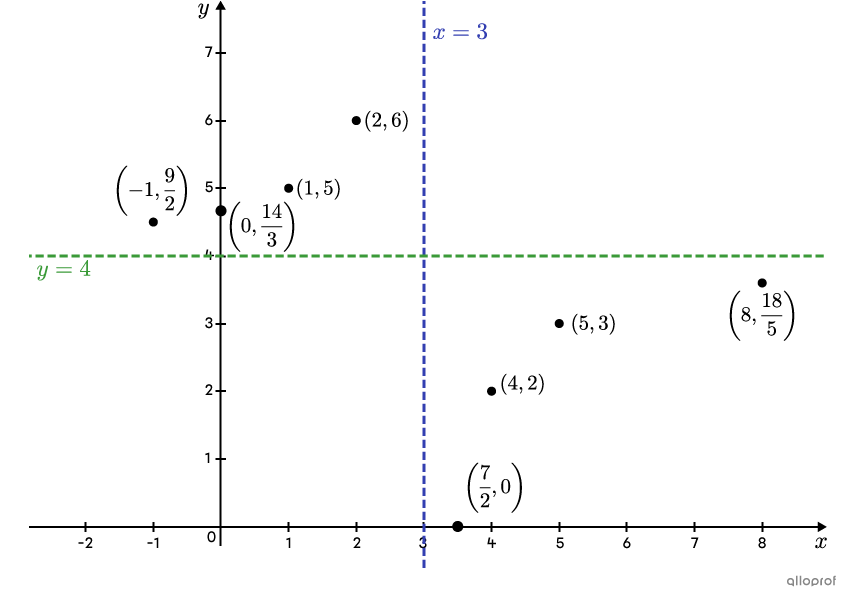
Trace la fonction rationnelle suivante. ||f(x) = \dfrac{4x-14}{x-3}||
-
Trouver les équations des asymptotes en utilisant les paramètres |h| et |k|
Pour déterminer la valeur des paramètres |h| et |k,| il faut transformer la règle sous la forme canonique en effectuant la division. ||\begin{align} \begin{aligned} 4x&-14\\ -(4x&-12)\\ \hline &\; \color{#ec0000}{-\;2} \end{aligned} \begin{aligned} \quad\vert\! &\underline{\quad \color{#3b87cd}{x-3}\quad}\\ &\ \ \ \color{#3a9a38}{+4}\\ \ \end{aligned} \end{align}||On obtient la règle suivante.||f(x)=\dfrac{\color{#ec0000}{-2}}{\color{#3b87cd}{x-3}}\color{#3a9a38}{+4}||L'équation de l'asymptote verticale est donnée par |\color{#3b87cd}{x=h}|, donc |\color{#3b87cd}{x=3}.|
L'équation de l'asymptote horizontale est donnée par |\color{#3a9a38}{y=k}|, donc |\color{#3a9a38}{y=4}.| -
Trouver les coordonnées de quelques points
Remarque : Pour calculer les coordonnées des points, on peut utiliser autant la règle sous la forme générale que sous la forme canonique.
|
On remplace |x| par |-1.| |
On remplace |x| par |0.| |
|---|---|
|
||\begin{align} |
||\begin{align} f(x) &= \dfrac{4x-14}{x-3}\\ f(0) &= \dfrac{4(0)-14}{(0)-3}\\ &= \dfrac{-14}{-3}\\ &=\dfrac{14}{3}\end{align}|| |
Avec cette démarche, on peut trouver d’autres couples.
|(1,5),| |(2,6),| |(4,2),| |(5,3),| |\left(8,\dfrac{18}{5}\right)|
Si on veut aussi trouver le zéro de la fonction, on remplace |f(x)| par |0| et on isole |x.| ||\begin{align} f(x) &= \dfrac{4x-14}{x-3}\\ 0 &= \dfrac{4x-14}{x-3}\\ 0 &= 4x-14\\ 14 &= 4x \\ \dfrac{7}{2} &= x\end{align}||On obtient le couple |\left(\dfrac{7}{2},0\right).|
-
Tracer les 2 asymptotes et situer les points trouvés dans le plan cartésien
-
Tracer les 2 courbes qui passent par les points situés précédemment et qui se rapprochent des asymptotes sans y toucher