La distance entre 2 points d'un plan cartésien correspond à la longueur du plus petit segment reliant ces points.
La distance entre les points |A| et |B| dans un plan cartésien, notée |\text{dist}(A,B),| correspond à la mesure du segment |\overline{AB}.| ||\text{dist}(A,B)=\text{m}\overline{AB}||Cette distance se calcule à l’aide de la formule suivante.
||\text{dist}(A,B)=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}||
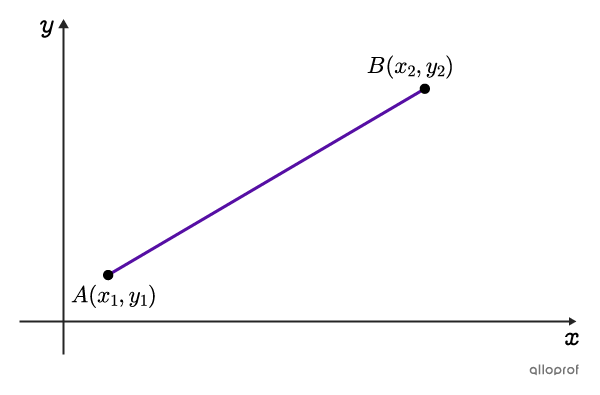
La formule de la distance entre 2 points provient directement du théorème de Pythagore.
Pour déterminer la distance séparant 2 points quelconques d'un plan cartésien, on considère que ces 2 points, |A| et |B,| sont les extrémités d'un segment correspondant à l'hypoténuse d'un triangle rectangle.
-
La différence des abscisses |(x_2-x_1)| donne la mesure de la cathète horizontale.
-
La différence des ordonnées |(y_2-y_1)| donne la mesure de la cathète verticale.
Ces 2 cathètes forment bel et bien un angle droit, car un segment horizontal et un segment vertical sont nécessairement perpendiculaires.
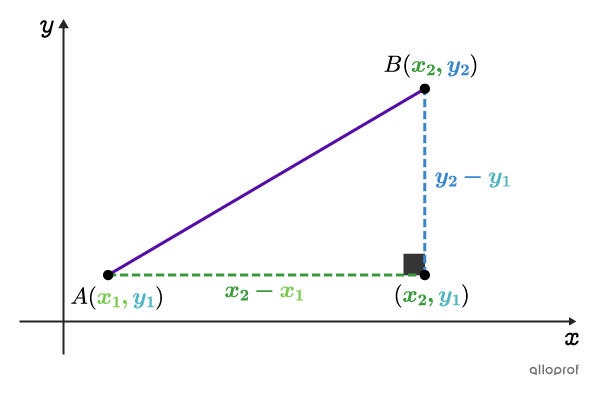
Le triangle formé est donc un triangle rectangle sur lequel on peut appliquer la relation de Pythagore |(c^2=a^2+b^2).| Il suffit de remplacer la cathète |a| par |x_2-x_1,| de remplacer la cathète |b| par |y_2-y_1| et de remplacer l’hypoténuse |c| par |\text{dist}(A,B).| ||\begin{alignat}{1}\boldsymbol{\color{#560fa5}c^2}\qquad&=\qquad\boldsymbol{\color{#3a9a38}a^2}&&+\qquad\boldsymbol{\color{#3b87cd}b^2}\\ \boldsymbol{\color{#560fa5}{\large(\normalsize\text{dist}(A,B)\!\large)}^2}&=\boldsymbol{\color{#3a9a38}{(x_2-\color{#7cca51}{x_1})}^2}&&+\boldsymbol{\color{#3b87cd}{(y_2-\color{#51b6c2}{y_1})}^2} \end{alignat}||En effectuant la racine carrée des 2 côtés de l’égalité afin d’isoler |\text{dist}(A,B),| on obtient bel et bien que la formule de la distance entre les points |A| et |B| est la suivante.||\boldsymbol{\color{#560fa5}{\text{dist}(A,B)}=\sqrt{\boldsymbol{\color{#3a9a38}{(x_2-\color{#7cca51}{x_1})}^2}+\boldsymbol{\color{#3b87cd}{(y_2-\color{#51b6c2}{y_1})}^2}}}||
-
Si |\text{dist}(A,B)=0,| alors |A=B.|
C’est ce qu’on appelle la propriété de séparation.
Si la distance entre 2 points est nulle, c’est que les 2 points sont confondus. -
|\text{dist}(A,B)=\text{dist}(B,A)|
C’est ce qu’on appelle la propriété de symétrie, qui repose sur le fait qu’une distance est toujours positive.
Par exemple, la distance entre Québec et Montréal est la même que la distance entre Montréal et Québec.
Ainsi, selon cette propriété, l'ordre des points dans la formule de la distance n'a pas d'importance. -
|\text{dist}(A,B)\le\text{dist}(A,C)+\text{dist}(C,B)|
C’est ce qu’on appelle l’inégalité triangulaire.
Si on se déplace d’un point |A| à un point |B| en passant par un autre point |(C),| il est impossible d’obtenir une distance totale plus courte que si on va directement du point |A| au point |B| sans passer par le point |C.|
On veut connaitre la distance entre les 2 points suivants : |A(1,2)| et |B(4,6).|
Il suffit d’appliquer la formule de la distance entre 2 points en respectant la priorité des opérations.||\begin{align}\text{dist}(A,B) &= \sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\\ &=\sqrt{(4-1)^2 + (6-2)^2}\\ &= \sqrt{3^2 + 4^2}\\ &= \sqrt{9+16}\\ &= \sqrt{25}\\ &=5 \end{align}||Réponse : La distance entre les points |A| et |B| est de |5| unités.
Dans le plan cartésien suivant, on veut connaitre la distance entre les points |P| et |Q.|
||\begin{align}\text{dist}(P,Q) &= \sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\\ &= \sqrt{(6--2)^2 + (-3--1)^2}\\ &= \sqrt{8^2 + (-2)^2}\\ &= \sqrt{64+4}\\ &= \sqrt{68}\\ &\approx 8{,}25\end{align}||
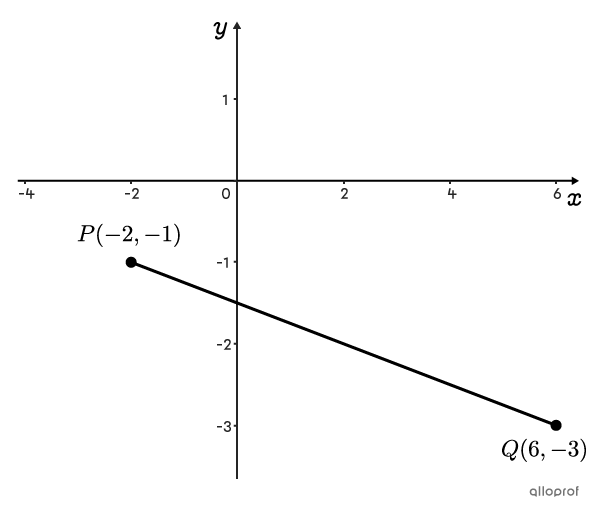
Réponse : La distance entre les points |P| et |Q| est approximativement de |8{,}25| unités.
Détermine le périmètre du quadrilatère |ABCD| suivant.
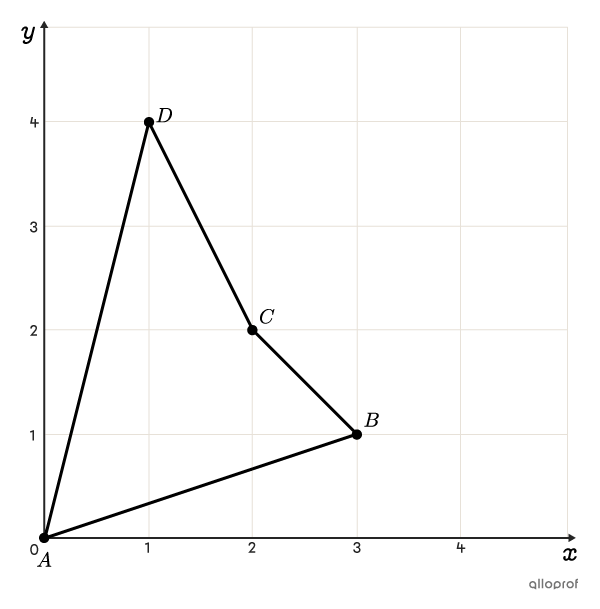
Pour répondre à cette question, il faut calculer la mesure de chaque segment du quadrilatère à partir des coordonnées des sommets, puis les additionner.
En observant la figure, on détermine que les coordonnées des 4 sommets sont les suivantes.
|A=(0,0),| |B=(3,1),| |C=(2,2)| et |D=(1,4)|
On utilise la formule de la distance entre 2 points pour calculer la mesure des 4 côtés du quadrilatère.
||\begin{align}\text{dist}(A,B) &= \sqrt{(3-0)^2 + (1-0)^2} \\&= \sqrt{3^2 + 1^2} \\ \text{m}\overline{AB}&= \sqrt{10} \end{align}||
||\begin{align}\text{dist}(B,C) &= \sqrt{(2-3)^2 + (2-1)^2} \\&= \sqrt{(-1)^2 + 1^2} \\ \text{m}\overline{BC}&= \sqrt{2} \end{align}||
||\begin{align}\text{dist}(C,D) &= \sqrt{(1-2)^2 + (4-2)^2} \\&= \sqrt{(-1)^2 + 2^2} \\ \text{m}\overline{CD}&= \sqrt{5} \end{align}||
||\begin{align}\text{dist}(D,A) &= \sqrt{(0-1)^2 + (0-4)^2} \\&= \sqrt{(-1)^2 + (-4)^2} \\ \text{m}\overline{DA}&= \sqrt{17} \end{align}||
On calcule le périmètre, qui correspond à la somme des mesures de chacun des côtés de la figure.||\begin{align}P&=\text{m}\overline{AB}+\text{m}\overline{BC}+\text{m}\overline{CD}+\text{m}\overline{DA}\\ &= \sqrt{10}+\sqrt{2}+\sqrt{5}+\sqrt{17}\\ &\approx 10{,}94\end{align}||Réponse : Le périmètre du quadrilatère |ABCD| mesure environ |10{,}94| unités.
Il est possible d’utiliser la formule de la distance entre 2 points pour faire des démonstrations en géométrie analytique.
Trouver la mesure d’un segment horizontal

||\begin{align}\text{dist}(A,B)&=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}\\&=\sqrt{(6-1)^{2}+(2-2)^{2}}\\ &=\sqrt{5^{2}+0^{2}}\\ &=\sqrt{25}\\ &=5 \end{align}||
Comme les 2 points sont à la même hauteur (même ordonnée), |y_2-y_1| vaut |0.| Il n’est donc pas nécessaire d’utiliser la formule de la distance entre 2 points. À la place, on peut utiliser la formule suivante.||\text{dist}(A,B)=\vert x_2-x_1\vert||
Trouver la mesure d’un segment vertical

||\begin{align}\text{dist}(A,B)&=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}\\&=\sqrt{(4-4)^{2}+(-2-3)^{2}}\\ &=\sqrt{0^{2}+(-5)^{2}}\\ &=\sqrt{25}\\ &=5 \end{align}||
Comme les 2 points ont la même abscisse, |x_2-x_1| vaut |0.| Il n’est donc pas nécessaire d’utiliser la formule de la distance entre 2 points. À la place, on peut utiliser la formule suivante.||\text{dist}(A,B)=\vert y_2-y_1\vert||
La formule de la distance entre 2 points peut être utilisée pour trouver une coordonnée manquante. En voici un exemple.
Sur la figure suivante, on connait la distance entre les points |A| et |B,| de même que les coordonnées de |A.| Cependant, on ne connait que l’ordonnée du point |B.|
Quelle est l’abscisse du point |B|?
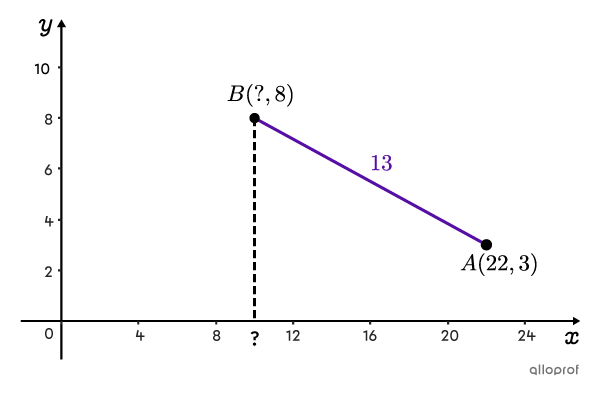
Il suffit d’écrire la formule de la distance entre 2 points et de remplacer |\text{dist}(A,B)| par |13,| |x_1| par |22,| |y_1| par |3| et |y_2| par |8.| Ensuite, il faut isoler |x_2| en réduisant l’équation et en effectuant les opérations inverses.||\begin{align}\text{dist}(A,B)&=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\\ 13 &= \sqrt{(x_2-22)^2 + (8-3)^2} \\ 13&= \sqrt{(x_2-22)^2+ 5^2} \\ 13^{\large\boldsymbol{\color{#ec0000}{2}}}&= \sqrt{(x_2-22)^2+ 25}^{\large\boldsymbol{\color{#ec0000}{\,2}}}\\ 169&= (x_2-22)^2+ 25\\ 169\boldsymbol{\color{#ec0000}{-25}}&= (x_2-22)^2+ 25\boldsymbol{\color{#ec0000}{-25}}\\ 144&= (x_2-22)^2\\ \color{#ec0000}{\sqrt{\color{black}{144}}}&= \color{#ec0000}{\sqrt{\color{black}{(x_2-22)^2}}}\\ \pm 12&=x_2-22\\ \pm 12\boldsymbol{\color{#ec0000}{+22}}&=x_2-22\boldsymbol{\color{#ec0000}{+22}}\\ &\Downarrow\\ x_2&=\pm 12+22\\ &\!\!\!\!\swarrow\; \searrow \\ \begin{aligned} x_2&=-12+22\\&=10 \end{aligned}\quad &\text{ou}\quad \begin{aligned} x_2&=12+22\\&=34 \end{aligned}\end{align}||Lorsqu’on extrait la racine carrée d’un nombre, il ne faut pas oublier qu’il y a toujours 2 possibilités : l’une positive et l’autre négative. C’est pourquoi on obtient 2 solutions possibles pour |x_2.| L’analyse du contexte nous permet généralement d’en éliminer une et de conserver l’autre. Ici, en observant la figure, on peut en déduire que la bonne solution est |x_2=10,| car le point |B| est situé à gauche du point |A.| L’abscisse de |B| est donc inférieure à celle de |A,| qui est de |22.|
Réponse : L’abscisse du point |B| est |10.|
Comme on l’a mentionné, c’est à cause de la racine carrée qu’il y a 2 solutions possibles. D’ailleurs, dans l’exemple précédent, si on avait oublié de tenir compte de la valeur négative au moment d’effectuer la racine carrée de |144,| on n’aurait même pas trouvé la bonne réponse.
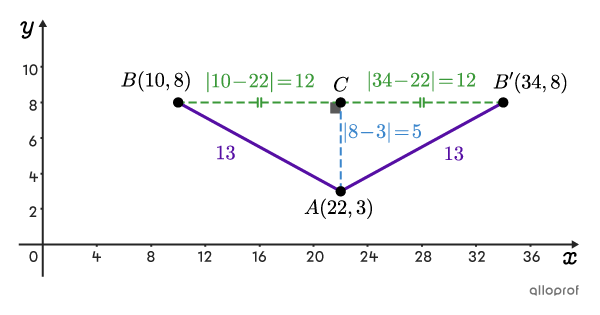
La figure suivante illustre comment il peut y avoir 2 positions possibles pour le point |B.| On sait que le point |A| est aux coordonnées |(22,3)| et que le point |B| est à une hauteur de |8| dans le plan cartésien. Toutefois, sans la figure, on ne pourrait pas savoir si le point |B| est à la gauche ou à la droite du point |A.|
Avec la figure présentée dans l’exemple précédent, il a été possible d’éliminer la solution |B’.| Toutefois, si la figure n’est pas fournie dans un exercice, il est important de donner les 2 réponses possibles.
Voici un exemple similaire, mais dans un problème écrit.
Le football américain est un jeu de tactique. Chaque jeu est planifié de manière précise.
Le coach Constantin a décidé de représenter un jeu dans un plan cartésien dont les coordonnées sont en verges.
Le ballon qui est placé au point |(0,0),| soit sur la ligne de mêlée, est mis en jeu par le joueur de centre. Pour ce faire, celui-ci remet le ballon à son quart-arrière, qui est situé directement derrière lui, à |4| verges de distance.
Ce dernier se déplace vers sa gauche d’un certain nombre de verges en gardant la possession du ballon, sans reculer ni avancer sur le terrain. Puis, lorsqu’il atteint exactement le bon point sur le terrain, il fait une passe de |17| verges pour atteindre son receveur de passe qui sera situé au point |(3,11)| à ce moment-là.
À partir de quel point le quart-arrière doit-il effectuer sa passe?
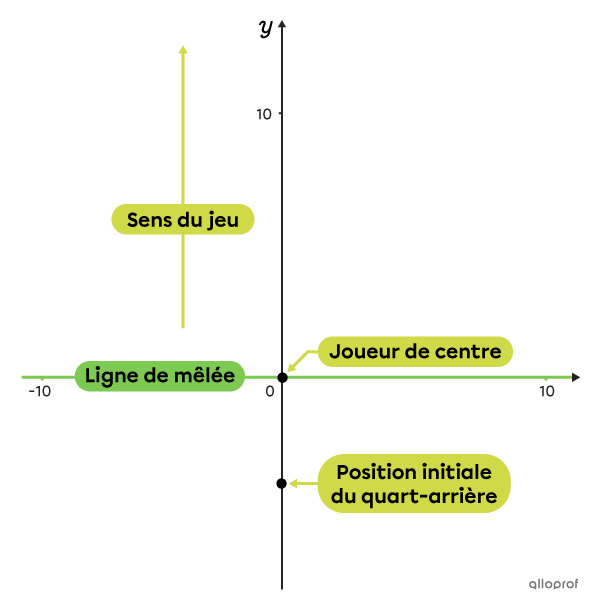
La 1re chose à faire pour résoudre un tel problème est de représenter la situation à l’aide d’une esquisse.
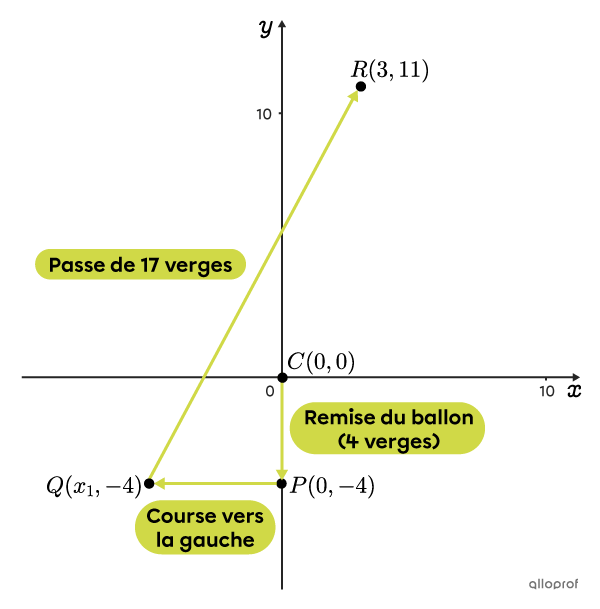
-
Le point |C| représente le joueur de centre qui remet le ballon au quart-arrière.
-
Le point |P| représente l’endroit dans la pochette où le quart-arrière prend possession du ballon, |4| verges derrière le joueur de centre.
-
Le point |Q| est l’endroit à partir duquel le quart-arrière effectue sa passe de |17| verges.
-
Le point |R| est l’endroit où le receveur doit être placé pour attraper la passe.
Le segment qui représente la passe est le segment |\overline{QR}.| On connait sa longueur de même que les coordonnées du point |R.| Cependant, pour le point |Q,| on ne connait que son ordonnée.
Pour trouver la coordonnée manquante, il faut écrire la formule de la distance entre 2 points et remplacer |\text{dist}(Q,R)| par |17,| |y_1| par |-4,| |x_2| par |3| et |y_2| par |11.| Ensuite, il faut isoler |x_1| en réduisant l’équation et en effectuant les opérations inverses.
||\begin{align}\text{dist}(Q,R)&=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\\ 17 &= \sqrt{(3-x_1)^2 + (11--4)^2} \\ 17&= \sqrt{(3-x_1)^2+ 15^2} \\ 17^{\large\boldsymbol{\color{#ec0000}{2}}}&= \sqrt{(3-x_1)^2+ 225}^{\large\boldsymbol{\color{#ec0000}{\,2}}}\\ 289&= (3-x_1)^2+ 225\\ 289\boldsymbol{\color{#ec0000}{-225}}&= (3-x_1)^2+ 225\boldsymbol{\color{#ec0000}{-225}}\\ 64&= (3-x_1)^2\\ \color{#ec0000}{\sqrt{\color{black}{64}}}&= \color{#ec0000}{\sqrt{\color{black}{(3-x_1)^2}}}\\ \pm 8&=3-x_1\\ &\Downarrow\\ x_1&=3\pm 8 \\ &\!\!\!\!\swarrow\; \searrow \\ \begin{aligned} x_1&=3-8\\&=-5 \end{aligned}\quad &\text{ou}\quad \begin{aligned} x_1&=3+8\\&=11 \end{aligned}\end{align}||
En observant la figure, on peut en déduire que la bonne solution est |x_1=-5,| car le point |Q| est situé à gauche de l’axe des |y.| Son abscisse doit donc être négative.
Réponse : Le quart-arrière doit effectuer sa passe à partir du point |(-5,-4).| Autrement dit, après avoir reçu le ballon, il doit se déplacer vers sa gauche de |5| verges avant de lancer le ballon.