The distance between two points on a Cartesian plane is the length of the shortest segment that connects these points.
The distance between points |A| and |B| on a Cartesian plane, denoted |\text{dist}(A,B),| corresponds to the measure of segment |\overline{AB}.|||\text{dist}(A,B)=\text{m}\overline{AB}||This distance is calculated using the following formula.
||\text{dist}(A,B)=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}||
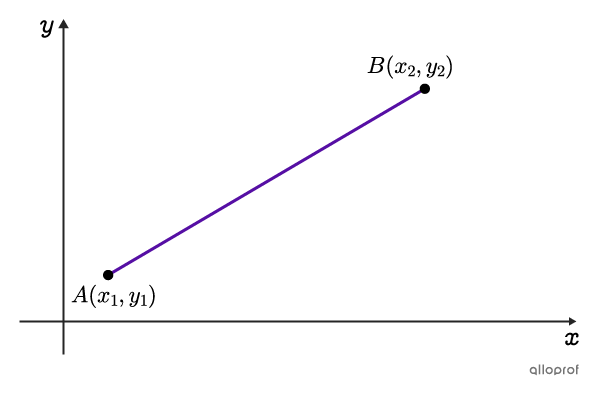
The distance between two points formula is derived directly from the Pythagorean theorem.
To find the distance separating any two points on a Cartesian plane, assume that these two points, |A| and |B,| are the endpoints of a segment corresponding to the hypotenuse of a right triangle.
-
The difference between the x-coordinates |(x_2-x_1)| gives the measure of the horizontal leg.
-
The difference between the y-coordinates |(y_2-y_1)| gives the measure of the vertical leg.
These 2 legs form a right angle, because all horizontal and vertical segments are perpendicular.

The triangle formed is therefore a right triangle, so we can apply the Pythagorean theorem |(c^2=a^2+b^2).| Simply replace the leg |a| by |x_2-x_1,| replace the leg |b| by |y_2-y_1| and replace the hypotenuse |c| by |\text{dist}(A,B).|||\begin{alignat}{1}\boldsymbol{\color{#560fa5}c^2}\qquad&=\qquad\boldsymbol{\color{#3a9a38}a^2}&&+\qquad\boldsymbol{\color{#3b87cd}b^2}\\ \boldsymbol{\color{#560fa5}{\large(\normalsize\text{dist}(A,B)\!\large)}^2}&=\boldsymbol{\color{#3a9a38}{(x_2-\color{#7cca51}{x_1})}^2}&&+\boldsymbol{\color{#3b87cd}{(y_2-\color{#51b6c2}{y_1})}^2} \end{alignat}||By taking the square root of both sides of the equation to isolate |\text{dist}(A,B),| the formula for the distance between points |A| and |B| is as follows:||\boldsymbol{\color{#560fa5}{\text{dist}(A,B)}=\sqrt{\boldsymbol{\color{#3a9a38}{(x_2-\color{#7cca51}{x_1})}^2}+\boldsymbol{\color{#3b87cd}{(y_2-\color{#51b6c2}{y_1})}^2}}}||
-
If |\text{dist}(A,B)=0,| then |A=B.|
This is known as the separation property.
If the distance between two points is zero, then the two points are coincident, or the same. -
|\text{dist}(A,B)=\text{dist}(B,A)|
This is known as the symmetry property, and it is based on the fact that any distance is always positive.
For example, the distance between Quebec City and Montreal is the same as the distance between Montreal and Quebec City.
Therefore, according to this property, the order of the points in the distance formula is irrelevant. -
|\text{dist}(A,B)\le\text{dist}(A,C)+\text{dist}(C,B)|
This is known as the triangle inequality.
If we move from point |A| to point |B| by passing through another point |(C),| it is impossible to get a shorter total distance than if we go directly from point |A| to point |B| without passing through point |C.|
What is the distance between the following two points: |A(1,2)| and |B(4,6)|?
Simply apply the distance between two points formula, while respecting the order of operations.||\begin{align}\text{dist}(A,B) &= \sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\\ &=\sqrt{(4-1)^2 + (6-2)^2}\\ &= \sqrt{3^2 + 4^2}\\ &= \sqrt{9+16}\\ &= \sqrt{25}\\ &=5 \end{align}||Answer: The distance between points |A| and |B| is |5| units.
What is the distance between points |P| and |Q| on the following Cartesian plane?
||\begin{align}\text{dist}(P,Q) &= \sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\\ &= \sqrt{(6--2)^2 + (-3--1)^2}\\ &= \sqrt{8^2 + (-2)^2}\\ &= \sqrt{64+4}\\ &= \sqrt{68}\\ &\approx 8.25\end{align}||
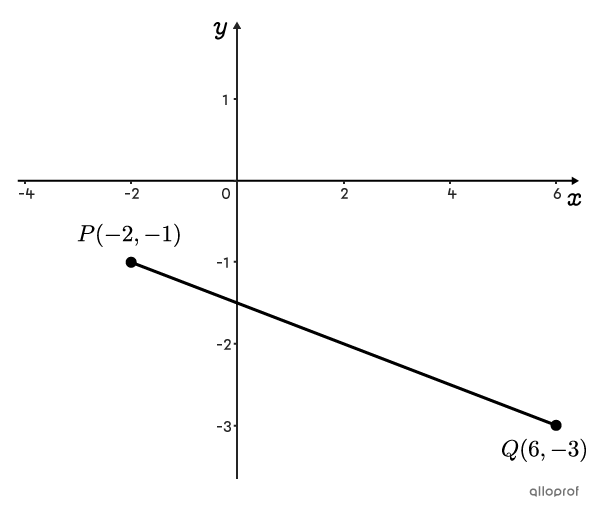
Answer: The distance between points |P| and |Q| is approximately |8.25| units.
Find the perimeter of the following quadrilateral |ABCD.|
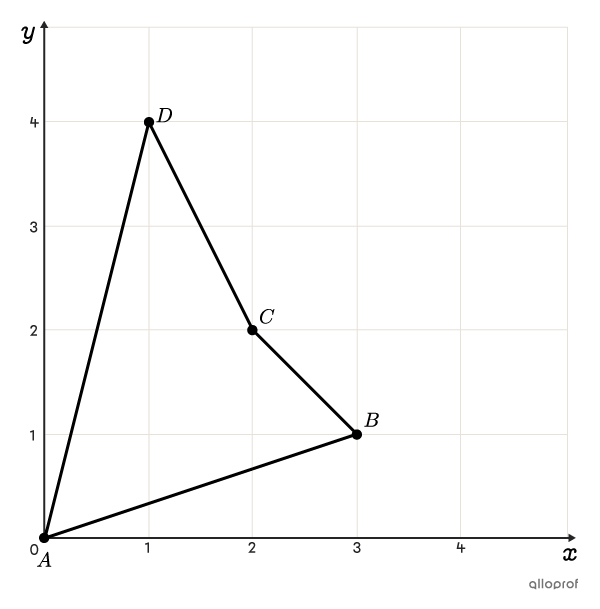
To answer this question, calculate the measure of each segment of the quadrilateral from the coordinates of the vertices, and then add them together.
By examining the figure, the coordinates of the 4 vertices are determined as being the following:
|A=(0,0),| |B=(3,1),| |C=(2,2)| and |D=(1,4)|
Apply the distance between two points formula to calculate the measures of all 4 sides of the quadrilateral.
||\begin{align}\text{dist}(A,B) &= \sqrt{(3-0)^2 + (1-0)^2} \\&= \sqrt{3^2 + 1^2} \\ \text{m}\overline{AB}&= \sqrt{10} \end{align}||
||\begin{align}\text{dist}(B,C) &= \sqrt{(2-3)^2 + (2-1)^2} \\&= \sqrt{(-1)^2 + 1^2} \\ \text{m}\overline{BC}&= \sqrt{2} \end{align}||
||\begin{align}\text{dist}(C,D) &= \sqrt{(1-2)^2 + (4-2)^2} \\&= \sqrt{(-1)^2 + 2^2} \\ \text{m}\overline{CD}&= \sqrt{5} \end{align}||
||\begin{align}\text{dist}(D,A) &= \sqrt{(0-1)^2 + (0-4)^2} \\&= \sqrt{(-1)^2 + (-4)^2} \\ \text{m}\overline{DA}&= \sqrt{17} \end{align}||
Calculate the perimeter, which is the sum of the figure's side measurements.||\begin{align}P&=\text{m}\overline{AB}+\text{m}\overline{BC}+\text{m}\overline{CD}+\text{m}\overline{DA}\\ &= \sqrt{10}+\sqrt{2}+\sqrt{5}+\sqrt{17}\\ &\approx 10.94\end{align}||Answer: The perimeter of quadrilateral |ABCD| measures approximately |10.94| units.
The distance between two points formula can be used in analytic geometry proofs.
Finding the measure of a horizontal segment

||\begin{align}\text{dist}(A,B)&=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}\\&=\sqrt{(6-1)^{2}+(2-2)^{2}}\\ &=\sqrt{5^{2}+0^{2}}\\ &=\sqrt{25}\\ &=5 \end{align}||
Since the two points have the same height (same y-coordinate), |y_2-y_1| equals |0.| Therefore, there's no need to use the formula for the distance between two points. Instead, the following formula can be used:||\text{dist}(A,B)=\vert x_2-x_1\vert||
Finding the measure of a vertical segment

||\begin{align}\text{dist}(A,B)&=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}\\&=\sqrt{(4-4)^{2}+(-2-3)^{2}}\\ &=\sqrt{0^{2}+(-5)^{2}}\\ &=\sqrt{25}\\ &=5 \end{align}||
Since the two points have the same x-coordinate, |x_2-x_1| equals |0.| Therefore, there's no need to use the formula for the distance between two points. Instead, the following formula can be used:||\text{dist}(A,B)=\vert y_2-y_1\vert||
The distance between two points formula can be used to find a missing coordinate. Here's an example.
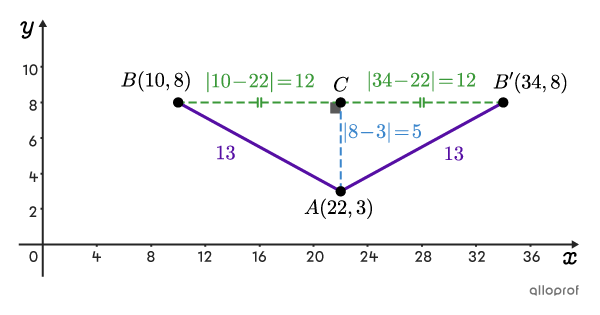
In the following diagram, the distance between points |A| and |B,| and the coordinates of |A| are known. However, only the y-coordinate of point |B| is given.
What is the x-coordinate of point |B|?

Simply write the formula for the distance between two points and replace |\text{dist}(A,B)| with |13,| |x_1| with |22,| |y_1,| with |3,| and |y_2| with |8.| Then isolate |x_2| by simplifying the equation and performing the inverse operations.||\begin{align}\text{dist}(A,B)&=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\\ 13 &= \sqrt{(x_2-22)^2 + (8-3)^2} \\ 13&= \sqrt{(x_2-22)^2+ 5^2} \\ 13^{\large\boldsymbol{\color{#ec0000}{2}}}&= \sqrt{(x_2-22)^2+ 25}^{\large\boldsymbol{\color{#ec0000}{\,2}}}\\ 169&= (x_2-22)^2+ 25\\ 169\boldsymbol{\color{#ec0000}{-25}}&= (x_2-22)^2+ 25\boldsymbol{\color{#ec0000}{-25}}\\ 144&= (x_2-22)^2\\ \color{#ec0000}{\sqrt{\color{black}{144}}}&= \color{#ec0000}{\sqrt{\color{black}{(x_2-22)^2}}}\\ \pm 12&=x_2-22\\ \pm 12\boldsymbol{\color{#ec0000}{+22}}&=x_2-22\boldsymbol{\color{#ec0000}{+22}}\\ &\Downarrow\\ x_2&=\pm 12+22\\ &\!\!\!\!\swarrow\; \searrow \\ \begin{aligned} x_2&=-12+22\\&=10 \end{aligned}\quad &\text{or}\quad \begin{aligned} x_2&=12+22\\&=34 \end{aligned}\end{align}||When taking the square root of a number, remember that there are always 2 possibilities: one positive and one negative. This is why there are 2 possible solutions for |x_2.| By analyzing the context, we can usually eliminate one and keep the other. Here, if we look at the figure, we can deduce that the correct solution is |x_2=10| because point |B| is to the left of point |A.| The x-coordinate of |B| is therefore less than that of |A,| which is |22.|
Answer: The x-coordinate of |B| is |10.|
As mentioned, because of the square root, there are 2 possible solutions. In fact, in the previous example, if we'd forgotten to take into account the negative value when calculating the square root of |144,| we wouldn't have found the right answer.
The following figure illustrates how there can be 2 possible positions for point |B.| We know that point |A| has the coordinates |(22,3)| and that point |B| is at a height of |8| on the Cartesian plane. However, without the figure, we wouldn't know if point |B| is to the left or right of point |A.|
With the figure shown in the previous example, it was possible to eliminate the solution |B'.| However, if the figure is not provided in an exercise, it is important to give both possible answers.
Here's a similar example, but in a word problem.
American football is a game of tactics. Each play is planned precisely.
Coach Constantin has decided to represent a game on a Cartesian plane whose coordinates are in yards.
The ball, which is placed at point |(0,0),| on the line of scrimmage, is put into play by the centre player. To do so, he passes the ball to his quarterback, who is directly behind him, |4| yards away.
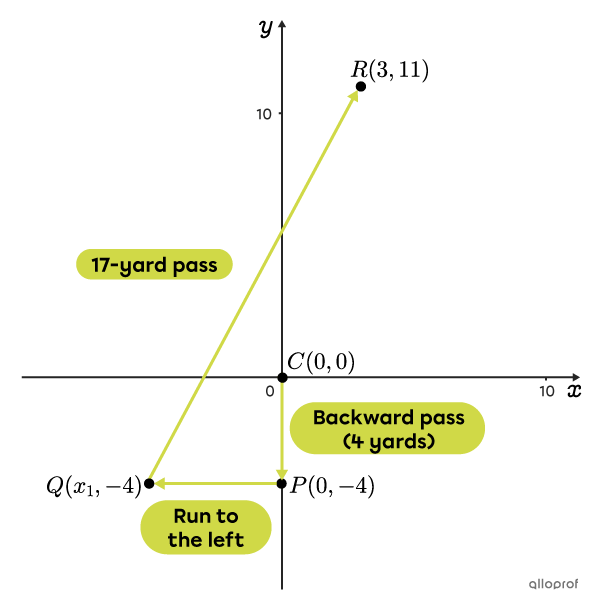
The quarterback moves a certain number of yards to his left while retaining possession of the ball, without moving backwards or forwards Then, when he reaches exactly the right point on the field, he completes a 17-yard pass to his receiver, who will be located at point |(3,11)| at that time.
From what point should the quarterback make his pass?
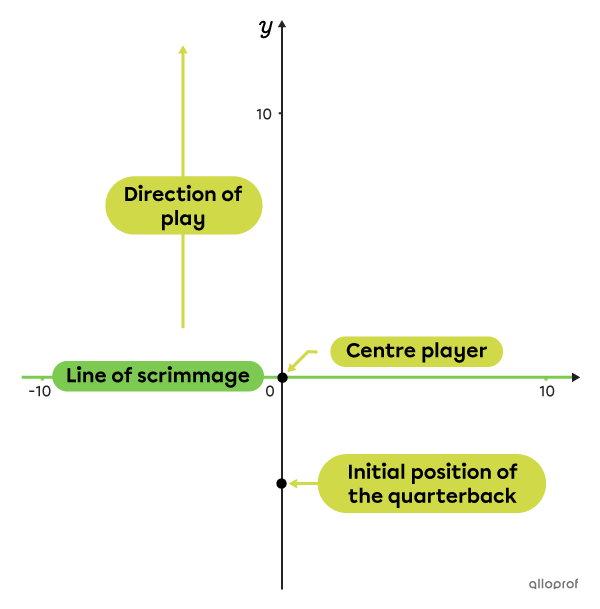
The first thing to do to solve a problem like this is to sketch the situation.
-
Point |C| represents the centre player who makes a backward pass to the quarterback.
-
Point |P| represents the spot in the pocket where the quarterback takes possession of the ball, |4| yards behind the centre player.
-
Point |Q| is the point from which the quarterback completes his 17-yard pass.
-
Point |R| is where the receiver must be positioned to catch the ball.
The segment that represents the pass is segment |\overline{QR}.| Its length is known, as are the coordinates of point |R.| However, for point |Q,| only its y-coordinate is known.
To find the missing coordinate, write the distance between two points formula and replace |\text{dist}(Q,R)| with |17,| |y_1| with |-4,| |x_2| with |3,| and |y_2| with |11.| Then isolate |x_1| by simplifying the equation and performing the inverse operations.
||\begin{align}\text{dist}(Q,R)&=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\\ 17 &= \sqrt{(3-x_1)^2 + (11--4)^2} \\ 17&= \sqrt{(3-x_1)^2+ 15^2} \\ 17^{\large\boldsymbol{\color{#ec0000}{2}}}&= \sqrt{(3-x_1)^2+ 225}^{\large\boldsymbol{\color{#ec0000}{\,2}}}\\ 289&= (3-x_1)^2+ 225\\ 289\boldsymbol{\color{#ec0000}{-225}}&= (3-x_1)^2+ 225\boldsymbol{\color{#ec0000}{-225}}\\ 64&= (3-x_1)^2\\ \color{#ec0000}{\sqrt{\color{black}{64}}}&= \color{#ec0000}{\sqrt{\color{black}{(3-x_1)^2}}}\\ \pm 8&=3-x_1\\ &\Downarrow\\ x_1&=3\pm 8 \\ &\!\!\!\!\swarrow\; \searrow \\ \begin{aligned} x_1&=3-8\\&=-5 \end{aligned}\quad &\text{or}\quad \begin{aligned} x_1&=3+8\\&=11 \end{aligned}\end{align}||
From the figure, it can be deduced that the correct solution is |x_1=-5,| because point |Q| is to the left of the y-axis, so its x-coordinate must be negative.
Answer: The quarterback must complete his pass from point |(-5,-4).| In other words, after receiving the ball, he must move |5| yards to his left before throwing the ball.