La comparaison des nombres rationnels permet de situer ces nombres les uns par rapport aux autres. On peut alors les placer en ordre croissant ou décroissant.
Comme les nombres rationnels peuvent être exprimés en notation fractionnaire ou en notation décimale, il est probable que, dans certaines situations, on demande de placer en ordre des nombres rationnels exprimés sous deux formes. Pour bien réussir à placer ces nombres en ordre, on doit s'assurer de maîtriser certaines notions.
Il existe plusieurs méthodes permettant de placer en ordre des nombres rationnels exprimés sous 2 formes. En voici une.
-
Déterminer si on doit placer les nombres en ordre croissant ou décroissant.
-
Choisir une forme d'écriture entre la notation fractionnaire et la notation décimale.
-
Exprimer chacun des nombres sous la même forme.
-
Selon la forme choisie, utiliser l'une des méthodes suivantes pour placer les nombres dans l'ordre désiré.
- Notation fractionnaire
Méthode 1 : À l'aide d'un dénominateur commun
Méthode 2 : À l'aide de la droite numérique
- Notation décimale
Méthode 1 : À l'aide des valeurs de positions
Méthode 2 : À l'aide de la droite numérique -
Remettre les nombres sous leur forme initiale.
Place en ordre croissant les nombres rationnels suivants.||1\dfrac{7}{8}\quad\dfrac{3}{5}\quad1{,}3\quad0{,}85\quad\dfrac{7}{2}\quad3{,}1\quad2{,}7||
-
Déterminer si on doit placer les nombres en ordre croissant ou décroissant
Tel que mentionné dans l'énoncé, les nombres doivent être placés en ordre croissant, c'est-à-dire du plus petit au plus grand.
-
Choisir une forme d'écriture entre la notation fractionnaire et la notation décimale
Généralement, il est plus facile d'exprimer chacun des nombres rationnels en notation décimale.
-
Exprimer chacun des nombres sous la même forme
On exprime en notation décimale les nombres écrits en notation fractionnaire.||1\dfrac{7}{8}=1{,}875\qquad\dfrac{3}{5}=0{,}6\qquad\dfrac{7}{2}=3{,}5||
-
Utiliser l'une des méthodes présentées pour placer les nombres dans l'ordre désiré
Prenons la méthode de la droite numérique pour les nombres rationnels exprimés en notation décimale.
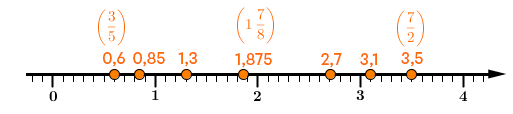
On obtient l'ordre croissant suivant.||0{,}6<0{,}85<1{,}3<1{,}875<2{,}7<3{,}1<3{,}5||
-
Remettre les nombres sous leur forme initiale
La réponse finale ressemble à ceci.||\dfrac{3}{5}<0{,}85<1{,}3<1\dfrac{7}{8}<2{,}7<3{,}1<\dfrac{7}{2}||