La comparaison des nombres rationnels exprimés en notation fractionnaire permet de situer ces nombres les uns par rapport aux autres. On peut alors les placer en ordre croissant ou décroissant.
Pour bien comprendre ce qui sera abordé dans cette section et pour être en mesure de placer en ordre les nombres en notation fractionnaire, il importe de se rappeler les types de fractions ainsi que la méthode à suivre pour exprimer une fraction en un nombre fractionnaire et l'inverse. De plus, il faut connaitre les fractions équivalentes et les méthodes de réduction.
L'ordre dans les nombres rationnels exprimés en notation fractionnaire peut être représentés de plusieurs façons. En voici une.
On utilise souvent l'image d'un tout divisé en parties égales pour représenter une fraction. Cette représentation peut aussi être utilisée pour représenter l'ordre.
Quelle fraction parmi les suivantes est la plus grande? ||\dfrac{3}{4}\qquad \qquad \dfrac{7}{8}||
On peut représenter cette situation à l'aide de deux figures séparées en parties égales.
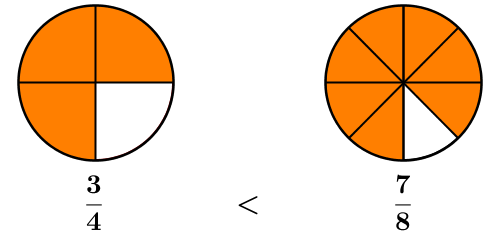
On remarque que |\dfrac{7}{8}| est plus grand que |\dfrac{3}{4}.| Pour s'en convaincre, on pourrait mettre les deux fractions sur le même dénominateur et comparer les numérateurs. On aurait :
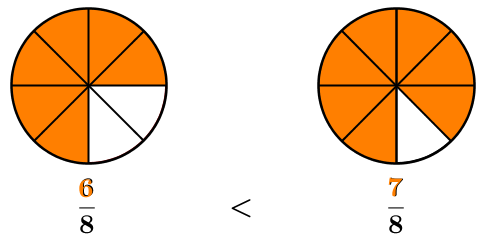
Une fois sur le même dénominateur, la fraction la plus grande détient le plus grand numérateur.
Dans le cas où nous avons des nombres fractionnaires, la représentation est semblable.
Quel nombre fractionnaire est le plus grand? ||1\dfrac{2}{3}\qquad \qquad 1\dfrac{3}{4}||
On peut représenter cette situation à l'aide des figures suivantes.
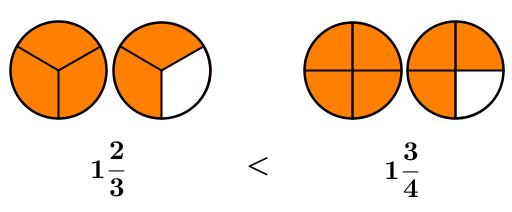
On remarque que |1\dfrac{3}{4}| est plus grand que |1\dfrac{2}{3}.| Pour s'en convaincre on pourrait mettre la partie fractionnaire sur le même dénominateur.
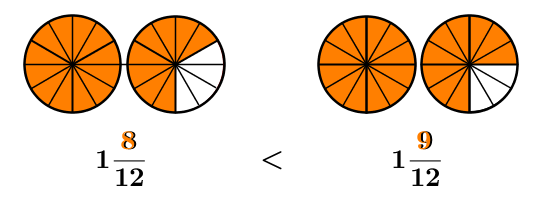
Lorsque l'on compare deux nombres fractionnaires ayant la même partie entière, il faut comparer leur partie fractionnaire. Une fois les parties fractionnaires sur le même dénominateur, le nombre fractionnaire le plus grand comprend le plus grand numérateur.
Si deux nombres fractionnaires n'ont pas la même partie entière, le plus grand est automatiquement celui qui détient la partie entière la plus grande. Par exemple : ||\color{red}{1}\dfrac{3}{4}\qquad < \qquad \color{red}{2}\dfrac{3}{4}||
Il existe quelques méthodes permettant de placer en ordre des nombres rationnels exprimés en notation fractionnaire. Nous en présenterons deux.
La recherche d'un dénominateur commun permet d'ordonner ces nombres de la façon suivante.
-
Exprimer les nombres fractionnaires en fraction, s'il y a lieu.
-
Déterminer le dénominateur commun à toutes les fractions.
-
Exprimer les fractions initiales en fractions équivalentes portant le dénominateur commun.
-
Placer les fractions en ordre selon l'ordre désiré en se fiant aux numérateurs uniquement.
-
Remettre les fractions sous leur forme initiale.
Pour déterminer le dénominateur commun à toutes les fractions, on peut utiliser la méthode du PPCM. En effet, le PPCM des dénominateurs d'un ensemble de fractions correspond à leur dénominateur commun.
Placer en ordre croissant les fractions suivantes. ||\dfrac{1}{8}\qquad \dfrac{3}{4}\qquad \dfrac{7}{10}\qquad \dfrac{1}{2}||
-
Exprimer les nombres fractionnaires en fraction
Comme il n'y a pas de nombres fractionnaires ici, on peut passer à l'étape suivante. -
Déterminer le dénominateur commun à toutes les fractions
En déterminant le PPCM des dénominateurs, on obtient : ||PPCM(8,4,10,2)=40||Le dénominateur commun est |40.| -
Exprimer les fractions initiales en fractions équivalentes portant le dénominateur commun
||\dfrac{1{\small\times 5}}{8{\small\times 5}}=\color{blue}{\dfrac{5}{40}}\qquad \dfrac{3{\small \times 10}}{4{\small \times 10}}=\color{green}{\dfrac{30}{40}}\qquad \dfrac{7{\small \times 4}}{10{\small \times 4}}=\color{purple}{\dfrac{28}{40}}\qquad \dfrac{1{\small \times 20}}{2{\small \times 20}}=\color{grey}{\dfrac{20}{40}}|| -
Placer les fractions en ordre selon l'ordre désiré en se fiant aux numérateurs uniquement
L'ordre croissant des numérateurs nous donne ceci : ||\color{blue}{\dfrac{5}{40}}\ <\ \color{grey}{\dfrac{20}{40}}\ <\ \color{purple}{\dfrac{28}{40}}\ <\ \color{green}{\dfrac{30}{40}}|| -
Remettre les fractions sous leur forme initiale
En ramenant les fractions sous leur forme initiale, on obtient l'ordre recherché. ||\dfrac{1}{8}\ <\ \dfrac{1}{2}\ <\ \dfrac{7}{10}\ <\ \dfrac{3}{4}||
Lorsqu'il y a des fractions négatives, on fonctionne de la même façon.
Place en ordre décroissant les nombres rationnels suivants.||1\dfrac{1}{3}\qquad -\dfrac{1}{2}\qquad -\dfrac{5}{6}\qquad \dfrac{13}{12}||
-
Exprimer les nombres fractionnaires en fraction
En exprimant le |1\dfrac{1}{3}| en fraction, on obtient : ||1\dfrac{1}{3}\ \Rightarrow\ \dfrac{4}{3}|| -
Déterminer le dénominateur commun à toutes les fractions
En déterminant le |PPCM| des dénominateurs, on obtient :||PPCM(3,2,6,12)=12||Le dénominateur commun est |12.| -
Exprimer les fractions initiales en fractions équivalentes portant le dénominateur commun||\dfrac{4{\small \times 4}}{3{\small \times 4}}=\color{blue}{\dfrac{16}{12}}\qquad -\dfrac{1{\small \times 6}}{2{\small \times 6}}=\color{green}{-\dfrac{6}{12}}\qquad -\dfrac{5{\small \times 2}}{6{\small \times 2}}=\color{purple}{-\frac{10}{12}}\qquad \dfrac{13}{12}=\color{grey}{\dfrac{13}{12}}||
-
Placer les fractions en ordre selon l'ordre désiré en se fiant aux numérateurs uniquement
Placer en ordre ces fractions revient à placer en ordre les numérateurs de celles-ci. Pour ce faire, on procède comme pour les nombres entiers. On obtient donc l'ordre décroissant suivant.||\color{blue}{\dfrac{16}{12}}\ >\ \color{grey}{\dfrac{13}{12}}\ >\ \color{green}{-\dfrac{6}{12}}\ >\ \color{purple}{-\dfrac{10}{12}}|| -
Remettre les fractions sous leur forme initiale
||1\dfrac{1}{3}\ >\ \dfrac{13}{12}\ >\ -\dfrac{1}{2}\ >\ -\dfrac{5}{6}||
Lorsqu'on a des fractions négatives, il peut être avantageux d'utiliser la droite numérique pour les placer en ordre.
Pour bien comprendre cette méthode, il faut être en mesure de placer des nombres exprimés en notation fractionnaire sur une droite numérique.
Pour placer un nombre exprimé en notation fractionnaire sur une droite numérique, on doit subdiviser la droite selon le dénominateur.

Prenons la fraction |\dfrac{2}{3}.| Cette fraction est comprise entre |0| et |1.| De plus, comme le dénominateur de la fraction est |3,| on devra subdiviser l'espace entre |0| et |1| en |3| parties égales.

Le numérateur de la fraction nous indique ensuite la position du nombre.

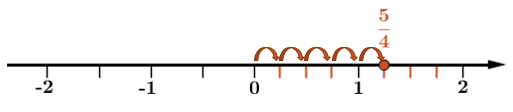
Si on a une fraction impropre, on subdivisera autant d'unités que nécessaire sur la droite numérique. Prenons |\dfrac{5}{4},| par exemple. Comme le dénominateur est |4,| on subdivise chaque unité en |4| parties égales. On place ensuite la fraction selon le numérateur.
Dans le cas où nous avons un nombre fractionnaire, on procède sensiblement de la même façon. La différence est qu'au lieu de partir de |0,| on partira de la partie entière du nombre fractionnaire.
Pour le nombre fractionnaire |{3}\dfrac{1}{2},| on n'a qu'à subdiviser l'espace entre |3| et |4| en |2| parties égales.

On procède de façon similaire pour les fractions et nombres fractionnaires négatifs.

Maintenant que l'on sait comment positionner un nombre exprimé en notation fractionnaire sur une droite numérique, on peut utiliser cette droite pour placer en ordre ces nombres.
-
Positionner chacun des nombres exprimés en notation fractionnaire sur une droite numérique.
-
Place les nombres selon l'ordre désiré, sachant que plus un nombre est positionné à droite plus il est grand.
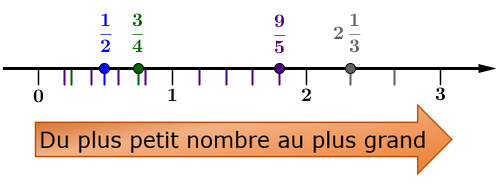
Place en ordre croissant les nombres rationnels suivants.||\dfrac{9}{5}\qquad \dfrac{1}{2}\qquad 2\dfrac{1}{3}\qquad \dfrac{3}{4}||
-
Positionner chacun des nombres exprimés en notation fractionnaire sur une droite numérique
En subdivisant convenablement la droite numérique, on positionne les nombres de la façon suivante.
-
Place les nombres selon l'ordre désiré sachant que plus un nombre est positionné à droite plus il est grand
On obtient l'ordre croissant suivant.||\dfrac{1}{2}\ <\ \dfrac{3}{4}\ <\ \dfrac{9}{5}\ <\ 2\dfrac{1}{3}||
On procède de la même façon avec les nombres rationnels négatifs exprimés en notation fractionnaire.