Rational numbers can be compared in order to place them in relation to each other. This allows them to be placed in ascending or descending order.
Since rational numbers can be expressed in both fractional and decimal notation, it is likely that, in some situations, you will be asked to order rational numbers that are expressed in both forms. To do so, it is important to have a good grasp of certain concepts.
Several methods exist for ordering rational numbers expressed in 2 different notations. Here is one:
-
Determine if the numbers should be placed in ascending or descending order.
-
Choose one notation (fractional or decimal).
-
Express each number in the same notation.
-
Depending on the chosen notation, use one of the following methods to place the numbers in the order required.
- Fractional notation
Method 1: Using a common denominator
Method 2: Using a number line
- Decimal notation
Method 1: Using place values
Method 2: Using a number line -
Return the numbers to their original form.
Place the following rational numbers in ascending order.||1\dfrac{7}{8}\quad\dfrac{3}{5}\quad1.3\quad0.85\quad\dfrac{7}{2}\quad3.1\quad2.7||
-
Determine if the numbers should be placed in ascending or descending order.
As mentioned in the problem statement, the numbers must be placed in ascending order, meaning from smallest to largest.
-
Choose one notation (fractional or decimal).
Generally speaking, it is easier to express each rational number in decimal notation.
-
Express each number in the same notation.
Numbers written in fractional notation are converted to decimal notation.||1\dfrac{7}{8}=1.875\qquad\dfrac{3}{5}=0.6\qquad\dfrac{7}{2}=3.5||
-
Use one of the presented methods to place the numbers in the desired order.
Here, the number line method is used for rational numbers expressed in decimal notation.
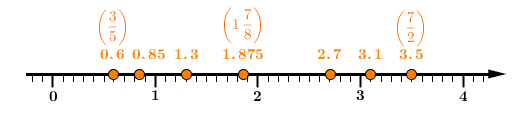
The following ascending order is obtained.||0.6<0.85<1.3<1.875<2.7<3.1<3.5||
-
Return the numbers to their original form.
The final answer is as follows:||\dfrac{3}{5}<0.85<1.3<1\dfrac{7}{8}<2.7<3.1<\dfrac{7}{2}||