L’ensemble des nombres rationnels, représenté par le symbole |\mathbb{Q},| regroupe tous les nombres qui correspondent à un quotient de 2 nombres entiers. Autrement dit, on peut les écrire sous la forme suivante.
||\dfrac{a}{b}||où |\{a,b\} \in \mathbb {Z}| et |b\neq 0|
Les nombres rationnels incluent l’ensemble des nombres entiers, et donc l’ensemble des nombres naturels. Cependant, contrairement aux nombres de ces 2 ensembles, les nombres rationnels peuvent avoir une partie décimale non nulle. Le développement décimal d’un nombre rationnel peut être fini ou infini et périodique.
Les nombres rationnels exprimés en notation décimale peuvent prendre 2 formes.
-
Un développement décimal fini
-
Un développement décimal infini et périodique
Le développement décimal fini
Le nombre |\dfrac{5}{4}| est un nombre rationnel. En effectuant la division du numérateur par le dénominateur, on obtient le nombre décimal |1{,}25.|
Ce nombre rationnel a un développement décimal fini, car son développement décimal est composé d’un nombre fini de chiffres (2 chiffres).
Le développement décimal infini et périodique
Le nombre |\dfrac{1}{3}| est un nombre rationnel. En effectuant la division du numérateur par le dénominateur, on obtient |0{,}333\,333\,333\dots|
Ce nombre rationnel a un développement décimal infini. Cependant, on remarque que le chiffre |3| se répète. Il s’agit de la période. On peut exprimer ce nombre rationnel de la façon suivante. ||\dfrac{1}{3}=0{,}\overline{3}||
Tous les nombres rationnels dont le développement décimal est fini sont regroupés dans un sous-ensemble appelé l’ensemble des nombres décimaux, qui est représenté par le symbole |\mathbb{D}.|
Les nombres rationnels dont le développement décimal est infini et périodique sont parfois appelés des nombres périodiques.
Sur une droite numérique, les nombres rationnels peuvent être représentés par des points situés à la position de tous les nombres qui peuvent s’écrire comme un quotient de 2 nombres entiers (une fraction).
Les points sur la droite numérique ci-dessous représentent quelques éléments de l’ensemble des nombres rationnels.

Les nombres rationnels |(\mathbb{Q})| forment un sous-ensemble des nombres réels et ils incluent les ensembles des nombres naturels et des nombres entiers. On peut utiliser la notation suivante pour représenter la relation entre ces ensembles. ||\mathbb N\subset\mathbb Z\subset \mathbb Q\subset \mathbb R||Voici la façon de le lire : « l’ensemble des nombres naturels est inclus dans l’ensemble des nombres entiers, qui est inclus dans celui des rationnels, qui est lui-même inclus dans l’ensemble des nombres réels ».
Voici un schéma qui démontre l’emplacement des nombres rationnels dans l’ensemble des nombres réels.
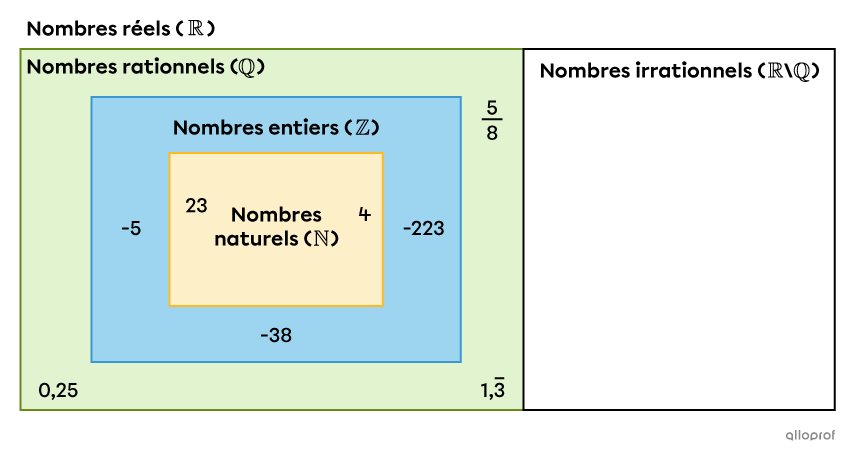
S'il est impossible d'écrire un nombre sous la forme d'une fraction de nombres entiers, celui-ci fait donc partie des nombres irrationnels.
-
Le nombre |\dfrac{3}{4}| est une fraction de la forme |\dfrac{a}{b}.| C’est donc un nombre rationnel.
-
Le nombre |0{,}25| est un nombre décimal à développement fini dont la forme |\dfrac{a}{b}| est |\dfrac{1}{4}.| Il s’agit donc aussi d’un nombre rationnel.
-
Le nombre |0{,}333\ldots=0{,}\overline{3}| est un nombre dont le développement décimal est infini et périodique. Il est donc un nombre rationnel. De plus, ce nombre peut s’exprimer sous forme de fraction : |\dfrac{1}{3}.|
-
Le nombre entier |-7| peut être écrit sous la forme |\dfrac{a}{b}| comme étant |-\dfrac{7}{1}.| Il est donc aussi un nombre rationnel.
-
Le nombre |2 \dfrac{1}{3}| est un nombre fractionnaire dont la forme |\dfrac{a}{b}| est |\dfrac{7}{3}| et dont le développement décimal est |2{,}\overline{3}.| Il fait donc partie de l’ensemble des nombres rationnels.
-
Les nombres |\sqrt2| et |\pi| sont des exemples de nombres qui ne peuvent pas s’exprimer sous la forme |\dfrac{a}{b},| où |a| et |b| sont des nombres entiers, et dont le développement décimal est infini et non périodique. Ils ne font donc pas partie de l’ensemble des nombres rationnels. Ce sont des nombres irrationnels.
-
En utilisant la notation appropriée, on obtient |0{,}25\in \mathbb{Q}| et |\sqrt2\notin \mathbb{Q}.|
-
On note |\mathbb{Q}^*| l’ensemble des nombres rationnels dont on a enlevé le nombre |0.|
-
On note |\mathbb{Q}_+| l’ensemble des nombres rationnels positifs.
-
On note |\mathbb{Q}_-| l’ensemble des nombres rationnels négatifs.
-
Il est possible de combiner ces notations. Par exemple, on note |\mathbb {Q}_-^*| l’ensemble des nombres rationnels négatifs sans le nombre |0.|
Pour ordonner des nombres rationnels, il est pratique de les transformer sous la même forme d’écriture (fractions, nombres fractionnaires ou nombres décimaux).