Cette MiniRécup est une révision des lois des logarithmes vues en secondaire 5. Les lois des exposants sont également utilisées dans cette vidéo. Tu peux visionner la MiniRécup sur les lois des exposants si tu as besoin d’un rappel.
Pour bien comprendre cette vidéo, tu dois être capable d’appliquer les lois des exposants. De plus, tu dois être familier(-ère) avec les mots de vocabulaire suivants : logarithme, base et argument.
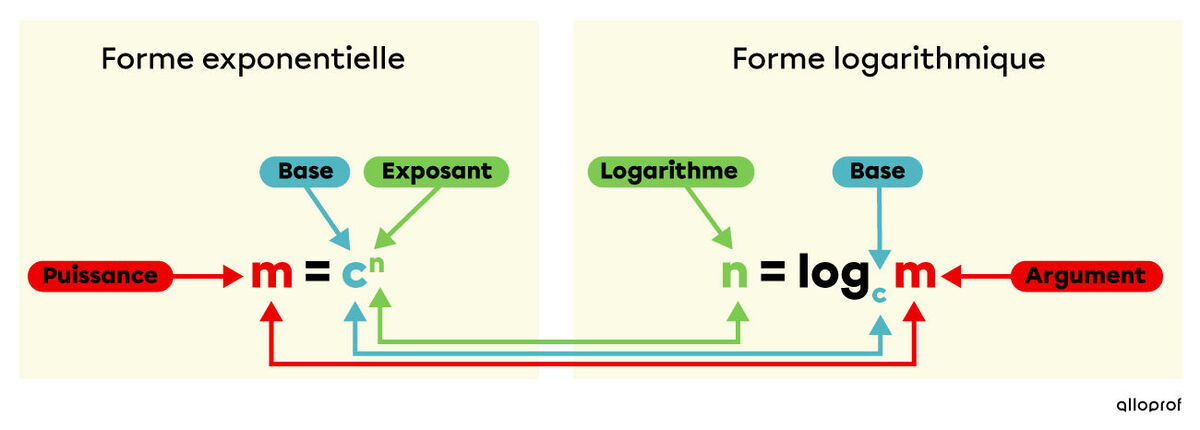
Lorsque tu fais des exercices sur les lois des logarithmes et des exposants, tu dois être capable de passer d’une forme à l’autre.
Un logarithme dont la base est |e| s’appelle un logarithme naturel et il est noté |\ln.|
Lorsque la base d’un logarithme est |10,| on le note simplement |\log.|
Le changement de base est une propriété qui permet de calculer la valeur d’un logarithme dont la base est différente de |e| ou de |10|.
Exemple : |\log_{9} 27 = \dfrac{\log_3 27}{\log_3 9} = \dfrac{3}{2}|
Voici un résumé des lois des logarithmes ainsi qu’un exemple pour chaque propriété :
|
Nom de la propriété |
Propriété | Exemple |
|---|---|---|
|
Le logarithme de 1 |
|\log_c (1) = 0| |
|\log_{9} 1 = 0| |
|
Le logarithme dont l’argument est identique à la base |
|\log_c (c) = 1| |
|\log_7 7= 1| |
|
Le logarithme d’une puissance |
|\log_c M^n = n\log_c M| |
|\log_2 9^5 = 5 \log_2 9| |
|
Le logarithme d’un produit |
|\log_c \left( M \times N \right) = \log_c M + \log_c N| |
|\begin{align} \log_3 48 &= \log_3 ( 6 \times 8 ) \\ &= \log_3 6 + \log_3 8 \end{align}| |
|
Le logarithme d’un quotient |
|\log_c \left(\dfrac{M}{N}\right) = \log_c M - \log_c N| |
|\begin{align} \log_{13} 45 - \log_{13} 5 &= \log_{13} \left(\dfrac{45}{5}\right) \\ &= \log_{13} 9 \end{align}| |
|
Le logarithme fractionnaire |
|\log_\frac{1}{c} M = -\log_c M| |
|\log_\frac{1}{4} 91 = -\log_4 91| |
|
Cas particulier |
|\log_c c^t = t| |
|\log_{3} 81 = \log_{3} 3^4 = 4| |