Cette MiniRécup porte sur les systèmes d’équations. Ses vidéos interactives, son résumé et ses exercices récapitulatifs te permettront de faire une courte révision à ce sujet.
Afin de bien comprendre cette MiniRécup, il faut que tu sois capable de tracer des droites dans un plan cartésien.
II est également utile de savoir ce que représentent le taux de variation (la pente) et l'ordonnée à l'origine dans la fonction affine pour suivre cette MiniRécup.
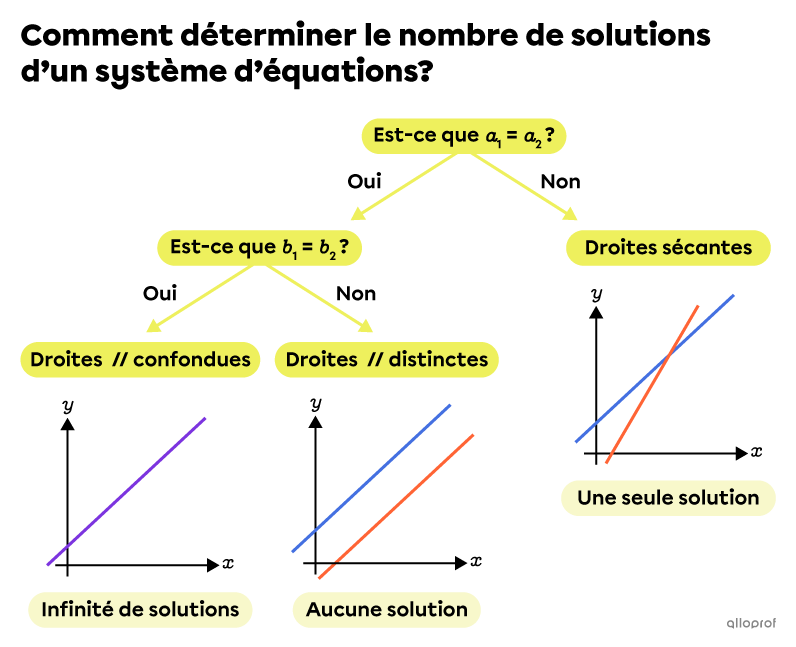
La méthode graphique et la table de valeurs
-
La méthode graphique permet de déterminer le nombre de solutions d’un problème. Le schéma précédent peut t’aider à déterminer le nombre de solutions d’un système d’équations.
-
On peut aussi résoudre un système d’équations à l’aide d’une table de valeurs. Pour ce faire, il faut trouver la valeur de |x| pour laquelle les valeurs de chaque |y| sont identiques.
Les méthodes algébriques
-
La méthode de comparaison permet de déterminer avec précision le couple solution quand la même variable est isolée dans les 2 équations du système d’équations.
Exemple : ||\begin{cases}y_1=5x-3\\y_2=2x+5 \end{cases}\\ \begin{align}\\y_1 &=y_2\\ 5x-3&= 2x+5\\ 3x&=8\\ x &=\dfrac{8}{3} \end{align}|| -
La méthode de substitution permet de déterminer avec précision le couple solution quand une variable est isolée dans l’une des 2 équations du système d’équations.
Exemple : ||\begin{cases}-5y+8x=3\\y=2x-5 \end{cases}\\ \begin{align}\\-5\color{#3a9a38}y+8x&=3\\ -5(\color{#3a9a38}{2x-5})+8x&=3 \\ -10x+25+8x&=3\\ -2x&=-22\\ x&=11 \end{align}|| -
La méthode de réduction permet de déterminer avec précision le couple solution quand aucune variable n’est isolée dans les 2 équations du système d’équations et que les 2 équations sont écrites de la même manière.
Exemple : ||\begin{cases}2y+5x=26 &\stackrel{\times 3}{\rightarrow}\ 6y+15x=78 \\ 3y-1x=5 &\stackrel{\times 2}{\rightarrow}\ 6y-2x=10\end{cases}\\ \begin{align}\\ \cancel{6y}+15x&=78\\ -\ (\cancel{6y}-\ \,2x&=10)\\ \hline 17x &=68\\ x&=4 \end{align}||
Remarque : Pour donner une solution complète à un système d’équations, il faut aussi calculer la valeur de l’autre variable en remplaçant la valeur trouvée dans l’une des 2 équations.
Finalement, n’oublie pas que lorsque tu as un problème écrit, tu dois commencer par identifier les variables utilisées pour poser tes équations.