The reaction rate is the variation in the quantity or concentration of reactants or products over time.
The following image shows the variation in the concentration of reactants and products over time for the hypothetical chemical reaction |2\ \text{A}\rightarrow \ \text{B}.|
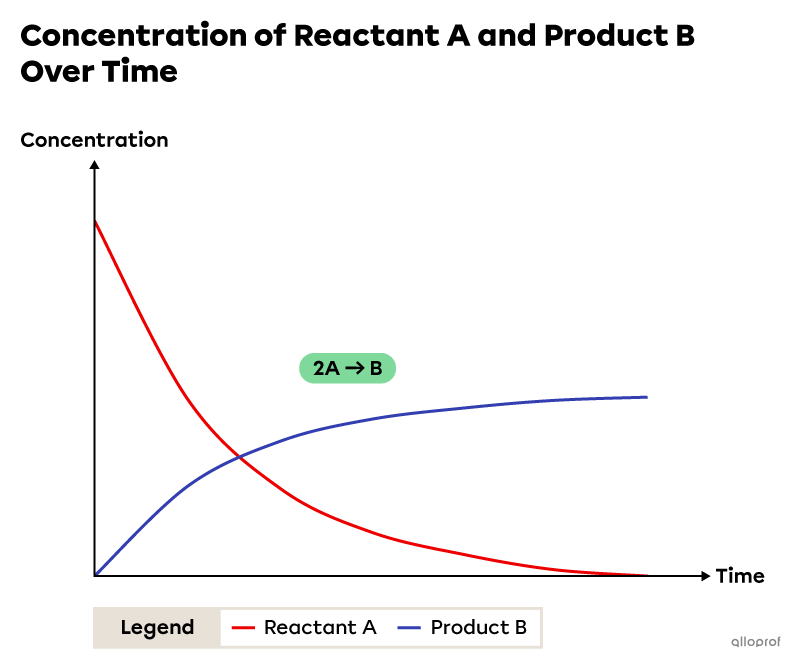
Over time, the concentration of reactant A decreases and the concentration of product B increases. Also, the variations in concentration are not constant. The concentrations vary rapidly at the start of the reaction and slowly at the end. This indicates that the reaction rate is higher at the beginning and lower at the end of the reaction. Finally, throughout the chemical reaction, the reaction rate with respect to reactant A is two times greater than the reaction rate with respect to product B. This is due to the proportion of substances involved in the chemical reaction. This proportion is revealed by the stoichiometric coefficients in the balanced chemical equation.
The reaction rate is generally measured in moles per litre per second |(\text{mol/L}{\cdot\text{s}}),| but it can also be measured in other units depending on the method used in the laboratory to measure the reaction rate.
Also, there are several types of mathematical equations for expressing a reaction rate. The following table describes them and their mathematical equations.
|
Reaction rate expression |
Description |
Mathematical equation |
|---|---|---|
|
It is used to calculate the variation in the quantity (or concentration) of a reactant or product over a given period. In a graph of concentration over time, it corresponds to the slope of the secant drawn between any two points on the curve. |
|r_{average}=\vert \text{slope}_{\text{secant}}\vert=\dfrac{\vert \Delta \text{Concentration of a reactant or product}\vert}{\Delta t}| |
|
|
It is used to calculate the reaction rate with respect to a reactant or product at a given time. In a graph of concentration over time, it corresponds to the slope of the tangent that touches the curve at a specific time. |
|r_{instantaneous}=\vert \text{slope}_{\text{tangent}}\vert=\dfrac{\vert \Delta \text{Concentration of a reactant or product}\vert}{\Delta t}| |
|
|
This is used to calculate the reaction rate, taking into account the concentration of the reactants and the reaction orders. |
For this hypothetical reaction |r=k[\text{A}]^m[\text{B}]^n| |
|
|
It is used to calculate the general reaction rate by dividing the rate with respect to one of the substances involved by its stoichiometric coefficient. |
For this hypothetical reaction |r_{\text{g}}=\dfrac{r_{\text{A}}}{a}=\dfrac{r_{\text{B}}}{b}=\dfrac{r_{\text{C}}}{c}=\dfrac{r_{\text{D}}}{d}| |
|
|
It is used to calculate the concentration of a reactant at any moment during the reaction. |
For this hypothetical order 0 reaction |\text{A}\rightarrow \text{B}| |[\text{A}]_t=-kt+[\text{A}]_0| |
The general reaction rate is an expression of the rate of reaction which takes into account the proportion of reactants and products involved in the chemical reaction. Those proportions are revealed by the stoichiometric coefficients of the balanced chemical equation.
For a hypothetical chemical reaction like |a\text{A}+b\text{B}\rightarrow c\text{C}+d\text{D},| the general reaction rate is expressed as follows.
||r_{\text{g}}=\dfrac{r_{\text{A}}}{a}=\dfrac{r_{\text{B}}}{b}=\dfrac{r_{\text{C}}}{c}=\dfrac{r_{\text{D}}}{d}||
where
|r_{\text{g}}:| general reaction rate in |\text{mol/s}| or in |\text{mol/L}\cdot\text{s}|
|r_{\text{A}}:| reaction rate with respect to the reactant A in |\text{mol/s}| or in |\text{mol/L}\cdot\text{s}|
|a:| stoichiometric coefficient of reactant A
|r_{\text{B}}:| reaction rate with respect to the reactant B in |\text{mol/s}| or in |\text{mol/L}\cdot\text{s}|
|b:| stoichiometric coefficient of reactant B
|r_{\text{C}}:| reaction rate with respect to the product C in |\text{mol/s}| or in |\text{mol/L}\cdot\text{s}|
|c:| stoichiometric coefficient of product C
|r_{\text{D}}:| reaction rate with respect to the product D in |\text{mol/s}| or in |\text{mol/L}\cdot\text{s}|
|d:| stoichiometric coefficient of product D
The chemical reaction between nitrogen gas |(\text{N}_2)| and hydrogen gas |(\text{H}_2)| produces ammonia |(\text{NH}_3)| according to the following equation.
||\text{N}_{2\text{(g)}}+3\ \text{H}_{2\text{(g)}}\rightarrow 2\ \text{NH}_{3\text{(g)}}||
After |3{.}0\ \text{hours},| |0{.}055\ \text{mol/L}| of |\text{NH}_3| is collected.
What is the general reaction rate?
-
Identify the given values.
|\begin{align}
\Delta[\text{NH}_3]&=0{.}055\ \text{mol/L}\\
\Delta t&=3{.}0\ \text{h}\times\dfrac{3\ 600\ \text{s}}{1\ \text{h}}\approx1{.}1\times10^{4}\ \text{s}\\\\
r_{\text{g}}&=\ ?\ \text{mol/L}\cdot\text{s}
\end{align}|
-
Calculate the reaction rate with respect to |\text{NH}_3|.
|\begin{align}
r_{\text{NH}_3}&=\dfrac{\Delta[\text{NH}_3]}{\Delta t}\\\\
r_{\text{NH}_3}&=\dfrac{0{.}055\ \text{mol/L}}{1{.}1\times10^{4}\ \text{s}}\\\\
r_{\text{NH}_3}&=5{.}0\times10^{-6}\ \text{mol/L}\cdot\text{s}
\end{align}|
-
Express the general reaction rate in relation to |v_{\text{NH}_3}.|
|\begin{align}
r_{\text{g}}&=\dfrac{r_{\text{N}_2}}{1}=\dfrac{r_{\text{H}_2}}{3}=\dfrac{r_{\text{NH}_3}}{2}\\\\
r_{\text{g}}&=\dfrac{r_{\text{NH}_3}}{2}
\end{align}|
-
Plug in the values and calculate the final answer.
|\begin{align}
r_{\text{g}}&=\dfrac{5{.}0\times10^{-6}\ \text{mol/L}\cdot\text{s}}{2}\\\\
r_{\text{g}}&=2{.}5\times10^{-6}\ \text{mol/L}\cdot\text{s}
\end{align}|
The general reaction rate is |2{.}5\times10^{-6}\ \text{mol/L}\cdot\text{s}.|
If the reaction rate with respect to one of the substances involved in a reaction is known, the general rate equation can be used to calculate the rate with respect to any other substances involved.
This is done by comparing the reaction rates with respect to each substance divided by their respective stoichiometric coefficients.
A reaction takes place according to the following unbalanced chemical equation.
||\text{PH}_{3\text{(g)}}\rightarrow \text{P}_{4\text{(g)}}+\text{H}_{2\text{(g)}}||
The reaction rate with respect to |\text{P}_4| is |6{.}\times10^{-4}\ \text{mol/L}\cdot\text{s}.|
a) What is is the reaction rate with respect to |\text{PH}_3?|
b) What is is the reaction rate with respect to |\text{H}_2?|
First, balance the chemical equation.
|4\ \text{PH}_{3\text{(g)}}\rightarrow \text{P}_{4\text{(g)}}+6\ \text{H}_{2\text{(g)}}|
a) Reaction rate with respect to |\text{PH}_3|
-
Identify the given values.
|\begin{align}
r_{\text{P}_4}&=6{.}0\times10^{-4}\ \text{mol/L}\cdot\text{s}\\
r_{\text{PH}_3}&=\ ?\ \text{mol/L}\cdot\text{s}
\end{align}|
-
Express the general reaction rate formula and isolate |r_{\text{PH}_3}.|
|\begin{align}
r_{\text{g}}=\dfrac{r_{\text{PH}_3}}{4}=\dfrac{r_{\text{P}_4}}{1}=\dfrac{r_{\text{H}_2}}{6}\Rightarrow \dfrac{r_{\text{PH}_3}}{4}&=\dfrac{r_{\text{P}_4}}{1}\\\\
r_{\text{PH}_3}&=r_{\text{P}_4}\times 4
\end{align}|
-
Plug in the values and calculate the final answer.
|\begin{align}
r_{\text{PH}_3}&=6{.}0\times10^{-4}\ \text{mol/L}\cdot\text{s}\times4\\
r_{\text{PH}_3}&=2{.}4\times10^{-3}\ \text{mol/L}\cdot\text{s}
\end{align}|
The reaction rate with respect to |\text{PH}_3| is |2{.}4\times10^{-3}\ \text{mol/L}\cdot\text{s}.|
b) Reaction rate with respect to |\text{H}_2|
-
Identify the given values.
|\begin{align}
r_{\text{P}_4}&=6{.}0\times10^{-4}\ \text{mol/L}\cdot\text{s}\\
r_{\text{H}_2}&=\ ?\ \text{mol/L}\cdot\text{s}
\end{align}|
-
Express the general reaction rate formula and isolate |r_{\text{H}_2}.|
|\begin{align}
r_{\text{g}}=\dfrac{r_{\text{PH}_3}}{4}=\dfrac{r_{\text{P}_4}}{1}=\dfrac{r_{\text{H}_2}}{6}\Rightarrow \dfrac{r_{\text{H}_2}}{6}&=\dfrac{r_{\text{P}_4}}{1}\\\\
r_{\text{H}_2}&=r_{\text{P}_4}\times 6
\end{align}|
-
Plug in the values and calculate the final answer.
|\begin{align}
r_{\text{H}_2}&=6{.}0\times10^{-4}\ \text{mol/L}\cdot\text{s}\times6\\
r_{\text{H}_2}&=3{.}6\times10^{-3}\ \text{mol/L}\cdot\text{s}
\end{align}|
The reaction rate with respect to |\text{H}_2| is |3{.}6\times10^{-3}\ \text{mol/L}\cdot\text{s}.|
A chemical reaction proceeds according to the following general equation.
||a\text{A}+b\text{B}\rightarrow c\text{C}||
The reaction rates for each substance are as follows.
|\begin{align}
r_{\text{A}}&=0{.}008\ 0\ \text{mol/L}\cdot\text{s}\\
r_{\text{B}}&=0{.}012\ 0\ \text{mol/L}\cdot\text{s}\\
r_{\text{C}}&=0{.}016\ 0\ \text{mol/L}\cdot\text{s}
\end{align}|
What are the stoichiometric coefficients |a,| |b| and |c|?
-
Using the expression for the general reaction rate, establish the following equations.
|r_{\text{g}}=\dfrac{r_{\text{A}}}{a}=\dfrac{r_{\text{B}}}{b}=\dfrac{r_{\text{C}}}{c}|
-
Consider the equality between |\dfrac{r_{\text{A}}}{a}| and |\dfrac{r_{\text{B}}}{b},| then isolate |a.|
|\begin{align}
\dfrac{r_{\text{A}}}{a}=\dfrac{r_{\text{B}}}{b}\Rightarrow a&=\dfrac{r_{\text{A}}\times b}{r_{\text{B}}}\\\\
a&=\dfrac{0{.}008\ 0\ \text{mol/L}\cdot\text{s}\times b}{0{.}012\ 0\ \text{mol/L}\cdot\text{s}}\\\\
a&=\dfrac{2}{3}b
\end{align}|
-
Consider the equality between |\dfrac{r_{\text{B}}}{b}| and |\dfrac{r_{\text{C}}}{c},| then isolate |b.|
|\begin{align}
\dfrac{r_{\text{B}}}{b}=\dfrac{r_{\text{C}}}{c}\Rightarrow b&=\dfrac{r_{\text{B}}\times c}{r_{\text{C}}}\\\\
b&=\dfrac{0{.}012\ 0\ \text{mol/L}\cdot\text{s}\times c}{0{.}016\ 0\ \text{mol/L}\cdot\text{s}}\\\\
b&=\dfrac{3}{4}c
\end{align}|
-
We end up with the following system of equations.
|\begin{align}
a&=\dfrac{2}{3}b\\\\
b&=\dfrac{3}{4}c
\end{align}|
-
To solve the system, let's assume that |b=1.|
|\begin{align}
a&=\dfrac{2}{3}\times1\Rightarrow a=\dfrac{2}{3}\\\\
b&=1\\\\
1&=\dfrac{3}{4}c\Rightarrow c=\dfrac{4}{3}
\end{align}|
-
To obtain integer stoichiometric coefficients, each is multiplied by |3.|
|\begin{align}
a&=\dfrac{2}{3}\times3=2\\\\
b&=1\times3=3\\\\
c&=\dfrac{4}{3}\times3=4
\end{align}|
The stoichiometric coefficients |a,| |b| and |c| are respectively |2,| |3| and |4.| The general equation for the chemical reaction is as follows.
|2\ \text{A}+3\ \text{B}\rightarrow4\ \text{C}|
The integrated rate law relates the rate constant, the concentration of the reactant and time. Among other things, it can be used to calculate the concentration of a reactant of the chemical reaction at any moment.
The equation of the integrated rate law varies according to the overall reaction order.
| Overall reaction order | Integrated rate law equation |
|---|---|
| |0| | |[\text{A}]_t=-kt+[\text{A}]_0| |
| |1| | |\ln[\text{A}]_t=-kt+\ln[\text{A}]_0| |
| |2| | |\dfrac{1}{[\text{A}]_t}=kt+\dfrac{1}{[\text{A}]_0}| |
where
|[\text{A}]_t:| concentration of reactant |\text{A}| at a given time of the reaction |(\text{mol/L})|
|[\text{A}]_0:| initial concentration of reactant |\text{A}| |(\text{mol/L})|
|t:| time passed at a given moment of the reaction |\text{s}|
|k:| rate constant (variable units depending on the order of reaction)
Consider the following reaction of order 0.
||\text{A}_{\text{(g)}}\rightarrow \text{B}_{\text{(g)}}||
The equation for the average reaction rate with respect to the reactant |\text{A}| is as follows.
|r_{\text{average}}=\dfrac{|\Delta[\text{A}]|}{\Delta t}|
The equation for the rate law is as follows.
|r=k[\text{A}]^0\Rightarrow r=k|
The following equation is obtained using the comparison method.
|\dfrac{\vert\Delta [\text{A}]\vert}{\Delta t}=k\Rightarrow\dfrac{\vert[\text{A}]_t-[\text{A}]_0\vert}{t-t_0}=k|
The initial reaction time |(t_0)| is assumed to be 0 seconds, so |t_0| can be removed from the equation.
|\dfrac{\vert[\text{A}]_t-[\text{A}]_0\vert}{t}=k|
Isolate the absolute value.
|\vert[\text{A}]_t-[\text{A}]_0\vert=kt|
Since |\text{A}| is a reactant, |[\text{A}]_t| is necessarily lower than |[\text{A}]_0,| so consider only the negative value of the absolute value.
The following equation is obtained.
|[\text{A}]_t-[\text{A}]_0=-kt|
Isolate |[\text{A}]_t| to obtain the integrated rate law as an affine function |(y =ax+b).|
|[\text{A}]_t=-kt+[\text{A}]_0|
This equation can be used to calculate the concentration of the reactant |\text{A}| at any moment of the reaction.
Nitrous oxide |(\text{N}_2\text{O})| breaks down into nitrogen gas |(\text{N}_2)| and oxygen gas |(\text{O}_2)| using a catalyst.
||2\ \text{N}_2\text{O}_{\text{(g)}}\xrightarrow{\text{Pt}}2\ \text{N}_{2\text{(g)}}+\text{O}_{2\text{(g)}}||
This is a reaction of order 0. Knowing that the initial concentration of |\text{N}_2\text{O}| is |0{.}010\ 0\text{mol/L}| and that the value of the reaction rate constant is |2{.}28\times10^{-5}\ \text{mol/L}\cdot\text{s},| what is the concentration of |\text{N}_2\text{O}| |250\ \text{s}| after the reaction has started?
-
Identify the given values.
|\begin{align}[\text{N}_2\text{O}]_{t=250}&=\ ?\ \text{mol/L}\\k&=2{.}28\times10^{-5}\ \text{mol/L}\cdot\text{s}\\t&=250\ \text{s}\\ [\text{N}_2\text{O}]_{0}&=0{.}010\ 0\ \text{mol/L}\end{align}|
-
Choose the integrated rate law for an order 0 reaction.
|[\text{A}]_t=-kt+[\text{A}]_0|
-
Plug in the values and calculate the final answer.
|\begin{align}[\text{N}_2\text{O}]_{t=250}&=(2{.}28\times10^{-5}\ \text{mol/L}\cdot\text{s}\times250\ \text{s})+0{.}010\ 0\ \text{mol/L}\\ [\text{N}_2\text{O}]_{t=250}&=0{.}004\ 3\ \text{mol/L}\end{align}|
After |250\ \text{s},| the concentration of |\text{N}_2\text{O}| is |0{.}004\ 3\ \text{mol/L}.|