La vitesse de réaction correspond à la variation de la quantité ou de la concentration des réactifs ou des produits en fonction du temps.
L’image suivante montre la variation de la concentration de réactifs et de produits en fonction du temps pour une réaction chimique quelconque du type |2\ \text{A}\rightarrow \ \text{B}.|
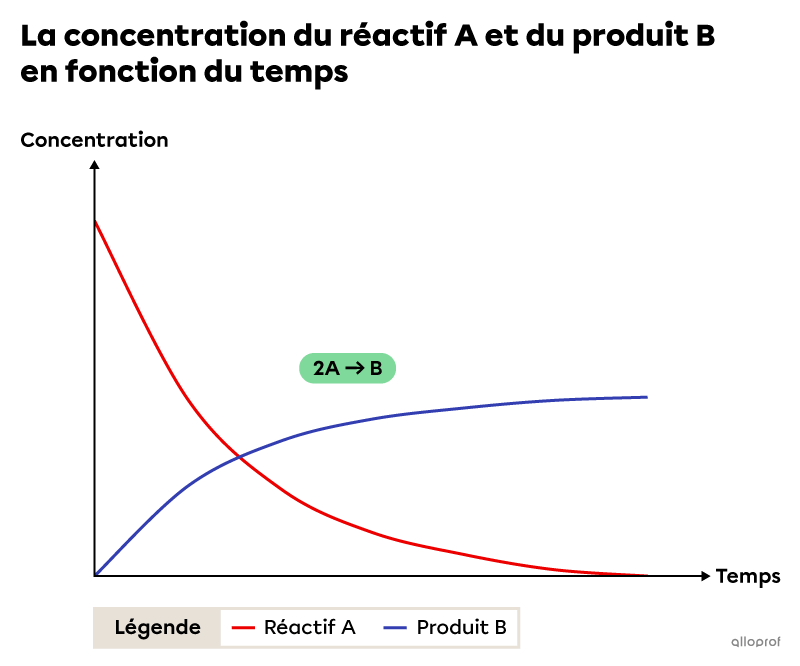
En fonction du temps, la concentration du réactif A diminue et la concentration du produit B augmente. De plus, on remarque que les variations des concentrations ne sont pas constantes. En effet, les concentrations varient rapidement au début de la réaction et elles varient lentement à la fin. Ceci indique que la vitesse de réaction est plus grande au début et plus petite à la fin de la réaction. Finalement, tout au long de la réaction chimique, la vitesse par rapport au réactif A est 2 fois plus grande que la vitesse par rapport au produit B. Cela est dû à la proportion des substances impliquées dans la réaction chimique. Cette proportion est révélée par les coefficients stœchiométriques de l’équation chimique balancée.
La vitesse de réaction se mesure généralement en moles par litre seconde |(\text{mol/L}{\cdot\text{s}}).| Elle peut aussi se mesurer à l’aide d’autres unités en fonction de la méthode employée en laboratoire pour déterminer la vitesse de réaction.
De plus, il existe plusieurs types d’équations mathématiques permettant d’exprimer la vitesse de réaction. Le tableau suivant décrit différentes expressions de la vitesse de réaction et leur équation mathématique.
|
Expression de la vitesse de réaction |
Description |
Équation mathématique |
|---|---|---|
|
Elle permet de calculer la variation de la quantité (ou de la concentration) d’un réactif ou d’un produit au cours d’une période déterminée. Dans un graphique de la concentration en fonction du temps, elle correspond à la pente de la sécante tracée entre deux points quelconques de la courbe. |
|v_{moyenne}=\vert \text{pente}_{\text{sécante}}\vert=\dfrac{\vert \Delta \text{Concentration d’un réactif ou d’un produit}\vert}{\Delta t}| |
|
|
Elle permet de calculer la vitesse par rapport à un réactif ou à un produit à un instant précis. Dans un graphique de la concentration en fonction du temps, elle correspond à la pente de la tangente qui touche la courbe à un temps donné. |
|v_{instantanée}=\vert \text{pente}_{\text{tangente}}\vert=\dfrac{\vert \Delta \text{Concentration d’un réactif ou d’un produit}\vert}{\Delta t}| |
|
|
Elle permet de calculer la vitesse en tenant compte de la concentration des réactifs et des ordres de réaction. |
Pour une réaction du type |a\text{A}+b\text{B}\rightarrow c\text{C}+d\text{D}|
|
|
|
Elle permet de calculer la vitesse générale d’une réaction en divisant la vitesse par rapport à l’une des substances impliquées par son coefficient stœchiométrique. |
Pour une réaction du type |a\text{A}+b\text{B}\rightarrow c\text{C}+d\text{D}|
|
|
|
Elle permet de calculer la concentration d’un réactif à tout moment de la réaction. |
Pour une réaction d’ordre 0 du type |\text{A}\rightarrow \text{B}|
|
La vitesse générale de réaction est une expression de la vitesse de réaction qui tient compte de la proportion des réactifs et des produits qui participent à la réaction chimique.
Les proportions selon lesquelles les substances sont impliquées dans une réaction chimique sont révélées par les coefficients stœchiométriques de l’équation chimique balancée.
Pour une réaction chimique quelconque |a\text{A}+b\text{B}\rightarrow c\text{C}+d\text{D},| la vitesse générale s’exprime de la façon suivante.
||v_{\text{g}}=\dfrac{v_{\text{A}}}{a}=\dfrac{v_{\text{B}}}{b}=\dfrac{v_{\text{C}}}{c}=\dfrac{v_{\text{D}}}{d}||
où
|v_{\text{g}}:| vitesse générale de réaction en |\text{mol/s}| ou en |\text{mol/L}\cdot\text{s}|
|v_{\text{A}}:| vitesse du réactif A en |\text{mol/s}| ou en |\text{mol/L}\cdot\text{s}|
|a :| coefficient stœchiométriques du réactif |\text{A}|
|v_{\text{B}}:| vitesse du réactif B en |\text{mol/s}| ou en |\text{mol/L}\cdot\text{s}|
|b :| coefficient stœchiométrique du réactif |\text{B}|
|v_{\text{C}}:| vitesse du produit C en |\text{mol/s}| ou en |\text{mol/L}\cdot\text{s}|
|c :| coefficient stœchiométrique du produit |\text{C}|
|v_{\text{D}}:| vitesse du produit D en |\text{mol/s}| ou en |\text{mol/L}\cdot\text{s}|
|d :| coefficient stœchiométrique du produit |\text{D}|
La réaction chimique entre le diazote |(\text{N}_2)| et le dihydrogène |(\text{H}_2)| produit de l’ammoniac |(\text{NH}_3)| selon l’équation suivante.
||\text{N}_{2\text{(g)}}+3\ \text{H}_{2\text{(g)}}\rightarrow 2\ \text{NH}_{3\text{(g)}}||
Au bout de |3{,}0\ \text{heures},| |0{,}055\ \text{mol/L}| de |\text{NH}_3| est récolté.
Quelle est la vitesse générale de réaction?
-
On identifie les données.
|\begin{align}
\Delta[\text{NH}_3]&=0{,}055\ \text{mol/L}\\
\Delta t&=3{,}0\ \text{h}\times\dfrac{3\ 600\ \text{s}}{1\ \text{h}}\approx1{,}1\times10^{4}\ \text{s}\\\\
v_{\text{g}}&=\ ?\ \text{mol/L}\cdot\text{s}
\end{align}|
-
On calcule la vitesse de réaction par rapport à |\text{NH}_3.|
|\begin{align}
v_{\text{NH}_3}&=\dfrac{\Delta[\text{NH}_3]}{\Delta t}\\\\
v_{\text{NH}_3}&=\dfrac{0{,}055\ \text{mol/L}}{1{,}1\times10^{4}\ \text{s}}\\\\
v_{\text{NH}_3}&=5{,}0\times10^{-6}\ \text{mol/L}\cdot\text{s}
\end{align}|
-
On exprime la formule de la vitesse générale de réaction en fonction de la vitesse de réaction par rapport à |\text{NH}_3.|
|\begin{align}
v_{\text{g}}&=\dfrac{v_{\text{N}_2}}{1}=\dfrac{v_{\text{H}_2}}{3}=\dfrac{v_{\text{NH}_3}}{2}\\\\
v_{\text{g}}&=\dfrac{v_{\text{NH}_3}}{2}
\end{align}|
-
On remplace les variables par les données et on résout l’équation.
|\begin{align}
v_{\text{g}}&=\dfrac{5{,}0\times10^{-6}\ \text{mol/L}\cdot\text{s}}{2}\\\\
v_{\text{g}}&=2{,}5\times10^{-6}\ \text{mol/L}\cdot\text{s}
\end{align}|
La vitesse générale de réaction est de |2{,}5\times10^{-6}\ \text{mol/L}\cdot\text{s}.|
Si l’on connait la vitesse par rapport à l’une des substances impliquées dans une réaction, l’équation de la vitesse générale permet de calculer la vitesse par rapport aux autres substances impliquées.
Pour ce faire, on compare les vitesses par rapport à chaque substance divisées par leur coefficient stœchiométrique respectif.
Une réaction se déroule selon l’équation chimique non balancée suivante.
||\text{PH}_{3\text{(g)}}\rightarrow \text{P}_{4\text{(g)}}+\text{H}_{2\text{(g)}}||
La vitesse par rapport à |\text{P}_4| est de |6{,}\times10^{-4}\ \text{mol/L}\cdot\text{s}.|
a) Quelle est la vitesse de réaction par rapport à |\text{PH}_3?|
b) Quelle est la vitesse de réaction par rapport à |\text{H}_2?|
D’abord, on effectue le balancement de l’équation chimique.
|4\ \text{PH}_{3\text{(g)}}\rightarrow \text{P}_{4\text{(g)}}+6\ \text{H}_{2\text{(g)}}|
a) La vitesse de réaction par rapport à |\text{PH}_3|
-
On identifie les données.
|\begin{align}
v_{\text{P}_4}&=6{,}0\times10^{-4}\ \text{mol/L}\cdot\text{s}\\
v_{\text{PH}_3}&=\ ?\ \text{mol/L}\cdot\text{s}
\end{align}|
-
On exprime la formule de la vitesse générale de réaction et on isole |v_{\text{PH}_3}.|
|\begin{align}
v_{\text{g}}=\dfrac{v_{\text{PH}_3}}{4}=\dfrac{v_{\text{P}_4}}{1}=\dfrac{v_{\text{H}_2}}{6}\Rightarrow \dfrac{v_{\text{PH}_3}}{4}&=\dfrac{v_{\text{P}_4}}{1}\\\\
v_{\text{PH}_3}&=v_{\text{P}_4}\times 4
\end{align}|
-
On remplace les variables par les données et on résout l’équation.
|\begin{align}
v_{\text{PH}_3}&=6{,}0\times10^{-4}\ \text{mol/L}\cdot\text{s}\times4\\
v_{\text{PH}_3}&=2{,}4\times10^{-3}\ \text{mol/L}\cdot\text{s}
\end{align}|
La vitesse de réaction par rapport à |\text{PH}_3| est de |2{,}4\times10^{-3}\ \text{mol/L}\cdot\text{s}.|
b) La vitesse de réaction par rapport à |\text{H}_2|
-
On identifie les données.
|\begin{align}
v_{\text{P}_4}&=6{,}0\times10^{-4}\ \text{mol/L}\cdot\text{s}\\
v_{\text{H}_2}&=\ ?\ \text{mol/L}\cdot\text{s}
\end{align}|
-
On choisit la formule de la vitesse générale et on isole |v_{\text{H}_2}.|
|\begin{align}
v_{\text{g}}=\dfrac{v_{\text{PH}_3}}{4}=\dfrac{v_{\text{P}_4}}{1}=\dfrac{v_{\text{H}_2}}{6}\Rightarrow \dfrac{v_{\text{H}_2}}{6}&=\dfrac{v_{\text{P}_4}}{1}\\\\
v_{\text{H}_2}&=v_{\text{P}_4}\times 6
\end{align}|
-
On remplace les variables par les données et on résout l’équation.
|\begin{align}
v_{\text{H}_2}&=6{,}0\times10^{-4}\ \text{mol/L}\cdot\text{s}\times6\\
v_{\text{H}_2}&=3{,}6\times10^{-3}\ \text{mol/L}\cdot\text{s}
\end{align}|
La vitesse de réaction par rapport à |v_{\text{H}_2}| est de |3{,}6\times10^{-3}\ \text{mol/L}\cdot\text{s}.|
Une réaction chimique se déroule selon l’équation générale suivante.
||a\text{A}+b\text{B}\rightarrow c\text{C}||
Les vitesses de réaction par rapport à chaque substance sont les suivantes.
|\begin{align}
v_{\text{A}}&=0{,}008\ 0\ \text{mol/L}\cdot\text{s}\\
v_{\text{B}}&=0{,}012\ 0\ \text{mol/L}\cdot\text{s}\\
v_{\text{C}}&=0{,}016\ 0\ \text{mol/L}\cdot\text{s}
\end{align}|
Détermine les coefficients stœchiométriques |a,| |b| et |c.|
-
À l’aide de l’expression de la vitesse générale de réaction, on établit les égalités suivantes.
|v_{\text{g}}=\dfrac{v_{\text{A}}}{a}=\dfrac{v_{\text{B}}}{b}=\dfrac{v_{\text{C}}}{c}|
-
Pour l’instant, on considère l’égalité entre |\dfrac{v_{\text{A}}}{a}| et |\dfrac{v_{\text{B}}}{b}| et on isole |a.|
|\begin{align}
\dfrac{v_{\text{A}}}{a}=\dfrac{v_{\text{B}}}{b}\Rightarrow a&=\dfrac{v_{\text{A}}\times b}{v_{\text{B}}}\\\\
a&=\dfrac{0{,}008\ 0\ \text{mol/L}\cdot\text{s}\times b}{0{,}012\ 0\ \text{mol/L}\cdot\text{s}}\\\\
a&=\dfrac{2}{3}b
\end{align}|
-
Ensuite on considère l’égalité entre |\dfrac{v_{\text{B}}}{b}| et |\dfrac{v_{\text{C}}}{c}| et on isole |b.|
|\begin{align}
\dfrac{v_{\text{B}}}{b}=\dfrac{v_{\text{C}}}{c}\Rightarrow b&=\dfrac{v_{\text{B}}\times c}{v_{\text{C}}}\\\\
b&=\dfrac{0{,}012\ 0\ \text{mol/L}\cdot\text{s}\times c}{0{,}016\ 0\ \text{mol/L}\cdot\text{s}}\\\\
b&=\dfrac{3}{4}c
\end{align}|
-
On se retrouve avec le système d’équations suivant.
|\begin{align}
a&=\dfrac{2}{3}b\\\\
b&=\dfrac{3}{4}c
\end{align}|
-
Pour résoudre le système, on peut supposer que |b=1.|
|\begin{align}
a&=\dfrac{2}{3}\times1\Rightarrow a=\dfrac{2}{3}\\\\
b&=1\\\\
1&=\dfrac{3}{4}c\Rightarrow c=\dfrac{4}{3}
\end{align}|
-
Pour obtenir des coefficients stœchiométriques entiers, on multiplie chacun d’eux par |3.|
|\begin{align}
a&=\dfrac{2}{3}\times3=2\\\\
b&=1\times3=3\\\\
c&=\dfrac{4}{3}\times3=4
\end{align}|
Les coefficients stœchiométriques |a,| |b| et |c| sont respectivement |2,| |3| et |4.| L’équation générale de la réaction chimique est la suivante.
|2\ \text{A}+3\ \text{B}\rightarrow4\ \text{C}|
La loi des vitesses intégrées met en relation la constante de vitesse, la concentration du réactif et le temps. Elle permet, entre autres, de calculer la concentration d’un réactif à tout moment de la réaction chimique.
L’équation de la loi des vitesses intégrées varie selon l’ordre global de réaction.
| Ordre global de la réaction | Équation de la loi des vitesses intégrées |
|---|---|
| |0| | |[\text{A}]_t=-kt+[\text{A}]_0| |
| |1| | |\ln[\text{A}]_t=-kt+\ln[\text{A}]_0| |
| |2| | |\dfrac{1}{[\text{A}]_t}=kt+\dfrac{1}{[\text{A}]_0}| |
où
|[\text{A}]_t :| concentration du réactif |\text{A}| à un moment donné de la réaction |(\text{mol/L})|
|[\text{A}]_0 :| concentration initiale du réactif |\text{A}| |(\text{mol/L})|
|t :| temps écoulé à un moment donné de la réaction |\text{s}|
|k :| constante de vitesse (unités variables selon l’ordre de réaction)
On considère la réaction d’ordre 0 suivante.
||\text{A}_{\text{(g)}}\rightarrow \text{B}_{\text{(g)}}||
L’équation de la vitesse moyenne par rapport au réactif |\text{A}| est la suivante.
|v_{\text{moyenne}}=\dfrac{|\Delta[\text{A}]|}{\Delta t}|
L’équation de la loi des vitesses est la suivante.
|v=k[\text{A}]^0\Rightarrow v=k|
En utilisant la méthode de comparaison, on obtient l’équation suivante.
|\dfrac{\vert\Delta [\text{A}]\vert}{\Delta t}=k\Rightarrow\dfrac{\vert[\text{A}]_t-[\text{A}]_0\vert}{t-t_0}=k|
On considère que le temps initial de la réaction |(t_0)| est à 0 seconde, on peut donc retirer |t_0| de l’équation.
|\dfrac{\vert[\text{A}]_t-[\text{A}]_0\vert}{t}=k|
Ensuite, on isole la valeur absolue.
|\vert[\text{A}]_t-[\text{A}]_0\vert=kt|
Puisque |\text{A}| est un réactif, |[\text{A}]_t| est nécessairement plus petite que |[\text{A}]_0,| alors on ne considère que la valeur négative de la valeur absolue.
On obtient l’équation suivante.
|[\text{A}]_t-[\text{A}]_0=-kt|
On isole |[\text{A}]_t| pour obtenir la loi des vitesses intégrées sous la forme d’une fonction affine |(y =ax+b).|
|[\text{A}]_t=-kt+[\text{A}]_0|
Cette équation permet de calculer la concentration du réactif |\text{A}| à tout moment de la réaction.
La décomposition de l’oxyde nitreux |(\text{N}_2\text{O})| en diazote |(\text{N}_2)| et en dioxygène |(\text{O}_2)| s’effectue à l’aide d’un catalyseur.
||2\ \text{N}_2\text{O}_{\text{(g)}}\xrightarrow{\text{Pt}}2\ \text{N}_{2\text{(g)}}+\text{O}_{2\text{(g)}}||
Il s’agit d’une réaction d’ordre 0. Sachant que la concentration initiale de |\text{N}_2\text{O}| est de |0{,}010\ 0\ \text{mol/L}| et que la valeur de la constante de vitesse est |2{,}28\times10^{-5}\ \text{mol/L}\cdot\text{s},| quelle est la concentration de |\text{N}_2\text{O}| |250\ \text{s}| après le début de la réaction?
-
On identifie les données.
|\begin{align}[\text{N}_2\text{O}]_{t=250}&=\ ?\ \text{mol/L}\\k&=2{,}28\times10^{-5}\ \text{mol/L}\cdot\text{s}\\t&=250\ \text{s}\\ [\text{N}_2\text{O}]_{0}&=0{,}010\ 0\ \text{mol/L}\end{align}|
-
On choisit l’équation des vitesses intégrées pour une réaction d’ordre 0.
|[\text{A}]_t=-kt+[\text{A}]_0|
-
On remplace les variables par les données et on résout l’équation.
|\begin{align}[\text{N}_2\text{O}]_{t=250}&=(2{,}28\times10^{-5}\ \text{mol/L}\cdot\text{s}\times250\ \text{s})+0{,}010\ 0\ \text{mol/L}\\ [\text{N}_2\text{O}]_{t=250}&=0{,}004\ 3\ \text{mol/L}\end{align}|
Après |250\ \text{s},| la concentration de |\text{N}_2\text{O}|est de |0{,}004\ 3\ \text{mol/L}.|