The set of integers, represented by the symbol |\mathbb{Z},| includes all natural numbers (positive integers) and their opposites (negative integers).||\mathbb{Z} = \{\ldots,-3,-2,-1,0,1,2,3\ldots\}||
Like natural numbers, integers have a decimal part of zero.
Opposite numbers have opposite signs and are located the same distance from |0.|
Opposite numbers are numbers with the same absolute value, but one is positive and the other is negative.
Furthermore, 2 numbers are said to be opposite when their sum is zero.
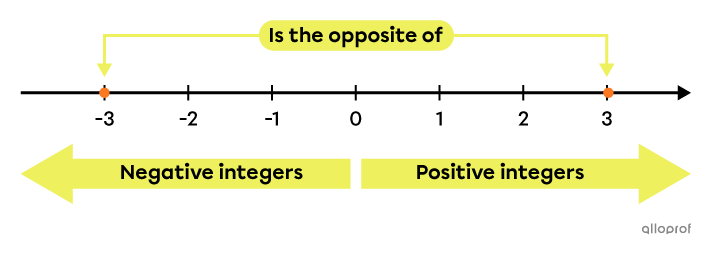
The number |-3| is the opposite of the number |3.| These 2 numbers are at the same distance from |0,| but have opposite signs.
Furthermore, the sum of these 2 numbers is zero, since |-3+3=0.|
Unlike negative numbers, which are always preceded by a "-" sign, positive numbers are generally written without a "+" sign.
The notion of the opposite of a number not only applies in |\mathbb{Z},| but in the majority of the real number subsets |(\mathbb{R}).|
On a number line, integers can be represented by points at the positive and negative number positions.
The orange dots on the number line below represent some of the elements in the set of integers.

The integers |(\mathbb{Z})| form a subset of the real numbers |(\mathbb{R})| and include the set of natural numbers |(\mathbb{N}).| We can use this notation to represent it.||\mathbb{N}\subset\mathbb{Z}||This reads: "The set of natural numbers is contained in the set of integers."
Here's a diagram that shows the location of the natural numbers |(\mathbb N)| inside the set of integers, |(\mathbb Z).|

-
The number |8,| the number |-92\ 683,| the number |-11| and their opposites are all integers.
-
The numbers represented by |-\dfrac{8}{4}| and |\dfrac{54}{9}| belong to the set of integers, because they correspond respectively to the numbers |-2| and |6.| The opposites of these numbers also belong to the set of integers.
-
The numbers |1521.46| and |-95.431| are not integers, as they have a non-zero decimal part. The same applies to the fraction |\dfrac{20}{3}.|
-
Using the appropriate notation, we write |-92\ 683\in\mathbb{Z}| and |1521.46\notin\mathbb{Z}.|
-
|\mathbb {Z}^*| denotes the set of integers excluding the number |0.| ||\mathbb {Z}^* = \{...,-3, -2, -1, 1, 2, 3, ... \}||
-
|\mathbb {Z}_+| is the set of all positive integers. In this case, it's the same as the set of natural numbers |(\mathbb N).| ||\mathbb {Z}_+ = \{ 0, 1, 2, 3, ... \} = \mathbb N||
-
|\mathbb {Z}_-| denotes the set of negative integers. ||\mathbb {Z}_- = \{ ... ,-5, -4, -3, -2, -1, 0 \}||
-
It is possible to combine these notations. For example, we denote |\mathbb {Z}_-^*| as the set of negative integers excluding the number |0.|
The floors in an elevator are represented by whole numbers. At ground level, you're on floor 0. If you take the elevator above ground level, you'll find yourself on floors 1, 2, 3, etc. If you choose to go below ground level, you'll find yourself on floors -1, -2, -3, etc.
A negative number is a number less than |0.|
Many everyday situations involve negative numbers.
Temperature
Temperature is measured using a thermometer graduated in degrees Celsius |(^\circ\text{C}).| During summer, the temperature is above |0^\circ\text{C};| and is therefore represented by positive numbers. However, in winter, the temperature falls below the freezing point of water and so it is lower than |0^\circ\text{C}.| Therefore, negative numbers are used to describe temperatures lower than |0^\circ\text{C}.|

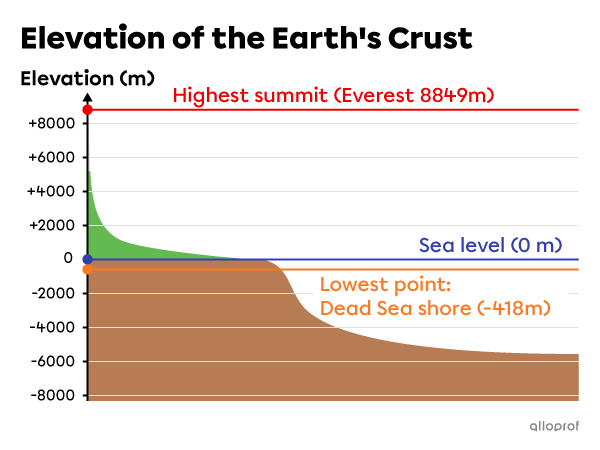
Altitude
Altitude is the vertical distance measured between a point on the Earth's surface and sea level. This height or depth is expressed on a scale graduated in metres. The |0| on the scale represents sea level.