The rule of a cosine function is |f(x)=a\cos\!\big(b(x-h)\big)+k.|
Parameter |a| is related to the amplitude.
Parameter |b| is related to the period.
Parameter |h| is related to the phase shift.
Parameter |k| is related to the axis of oscillation.
When looking for the rule of a sinusoidal function using the cosine function, we need to locate a cycle that begins at an extreme point (a maximum or a minimum) and ends at the same height. The point at the start of the chosen cycle corresponds to point |(h,k+A)| if it is a maximum and to point |(h,k-A)| if it is a minimum.

Since there are an infinite number of extremes for the same cosine function, there are an infinite number of possible values for |h| and |k.|
-
Determine |k| using the axis of oscillation.
-
Choose an extreme and determine |h.|
-
Determine one cycle starting from the chosen extreme.
-
Determine |\vert a\vert| from the amplitude.
-
Determine |b| from the period.
-
Determine the sign of |a.|
If the function begins at a maximum, |a| is positive.
If the function begins at a minimum, |a| is negative. -
Write the rule of the function.
Determine the rule of the cosine function that passes through points |(1.25,-0.25)| and |(2.75,-1.75)| which respectively represent maximum and minimum points.
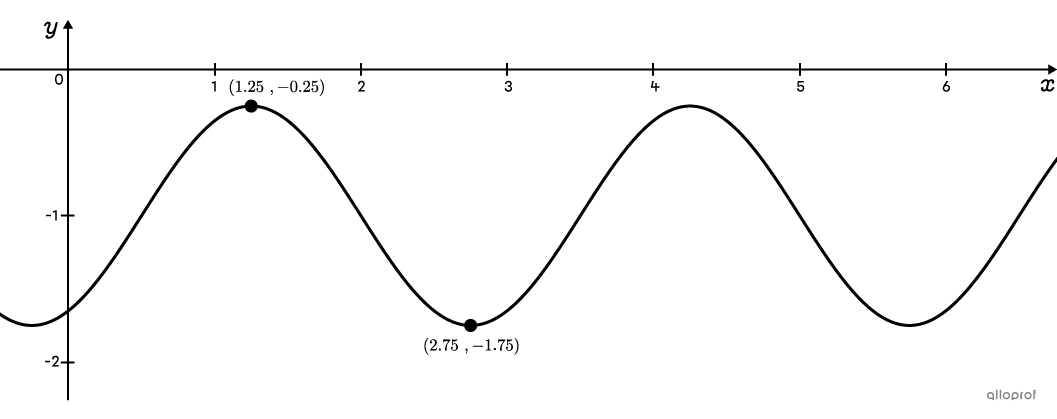
-
Determine |k| using the axis of oscillation.
To determine the value of |k,| use the following formula:||\begin{align}k&=\dfrac{\max+\min}{2}\\&=\dfrac{\color{#EC0000}{-0.25}+\color{#EC0000}{-1.75}}{2}\\&=-1\end{align}|| -
Choose an extreme point and determine |h.|
Let's take point |(1.25, -0.25)| as the extreme.||h=1.25||
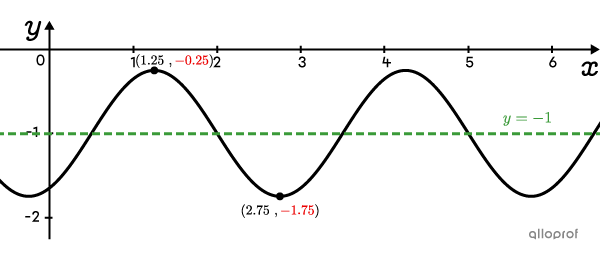
-
Determine one cycle starting from the chosen extreme.
Sketch a rectangle framing one cycle starting at point |(1.25, -0.25).| -
Determine |\vert a\vert| from the amplitude.
The absolute value of |a| is determined using the amplitude.||\begin{align}\vert a\vert&=\color{#fa7921}A\\&=\dfrac{\max-\min}{2}\\&=\dfrac{\color{#EC0000}{-0.25}-\color{#EC0000}{-1.75}}{2}\\&=\color{#fa7921}{0.75}\end{align}||
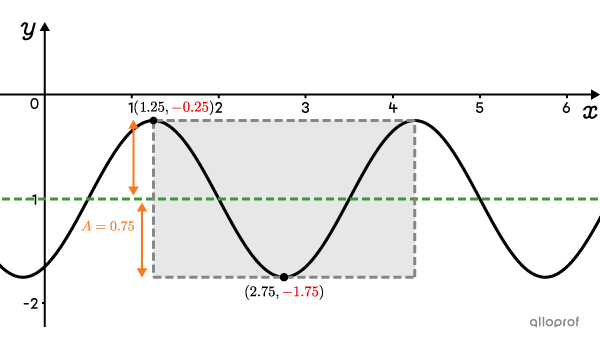
-
Determine |b| from the period.
The value of |b| is found using the period.
There is a half-period between a maximum and a minimum. To calculate the full period, proceed as follows:||\begin{align}\dfrac{1}{2}\color{#333fb1}p&=\color{#333fb1}{2.75}-\color{#333fb1}{1.25}\\\dfrac{1}{2}\color{#333fb1}p&=1.5\\ \color{#333fb1}p &= \color{#333fb1}3 \end{align}||
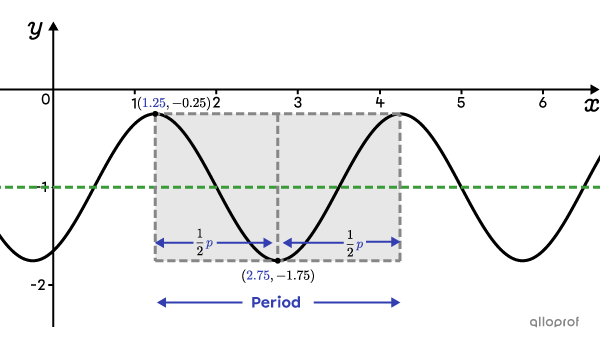
Now, we can determine |b.|||\begin{align}\color{#333fb1}p&=\dfrac{2\pi}{\vert b\vert}\\\color{#333fb1}{3}&=\dfrac{2\pi}{\vert b\vert}\ \Leftrightarrow\ \vert b\vert=\dfrac{2\pi}{3}\end{align}||Since the sign of |b| does not change the curve, the easiest thing to do is to choose its positive value.||b=\dfrac{2\pi}{3}||
-
Determine the sign of |a.|
Since the starting point of the cycle is a maximum, |a| is positive.||a>0|| -
Write the rule of the function.
The rule of the cosine function is |f(x)=0.75\cos\left(\dfrac{2\pi}{3}(x-1.25)\right)-1.|
Note: If the extreme point chosen in Step 1 is different, other answers are possible for the same graph.
In the last example, by choosing the maximum point |(1.25, -0.25),| the following rule was obtained:||f(x)=0.75\cos\left(\dfrac{2\pi}{3}(x-1.25)\right)-1||
If, instead, point |(2.75, -1.75)| had been chosen, the function would have started at a minimum, which means that |a| would have been negative. The following rule would then have been obtained:||f(x)=-0.75\cos\left(\dfrac{2\pi}{3}(x-2.75)\right)-1||An analysis of these rules shows that the values of |\vert a\vert,| |b| and |k| never change. The only differences between the rules are the value of |h| and the sign of |a.|

Here is an example where the complete cycle is not shown on the Cartesian plane.
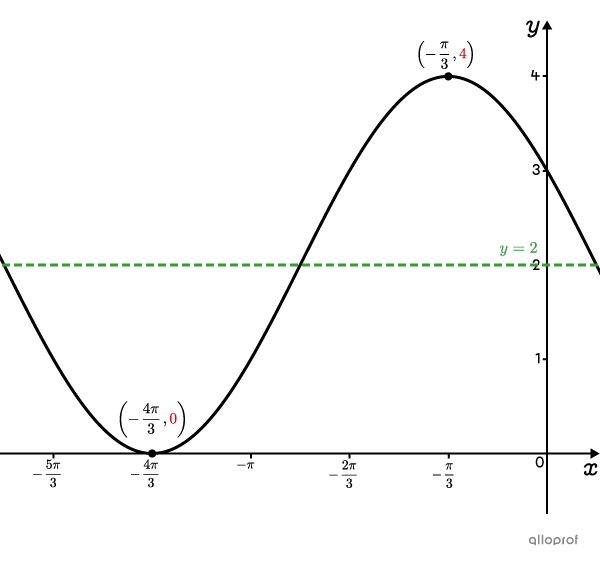
Determine the rule of the cosine function that passes through points |\left(-\dfrac{4\pi}{3},0\right)| and |\left(-\dfrac{\pi}{3},4\right)| which respectively represent a minimum and a maximum.

-
Determine |k| using the axis of oscillation.
To determine the value of |k,| use the following formula:||\begin{align}k&=\dfrac{\max+\min}{2}\\&=\dfrac{\color{#EC0000}{4}+\color{#EC0000}{0}}{2}\\&=2\end{align}|| -
Choose an extreme and determine |h.|
Let's take point |\left(-\dfrac{4\pi}{3},0\right)| as the extreme.||h=-\dfrac{4\pi}{3}||
-
Determine one cycle starting from the chosen extreme.
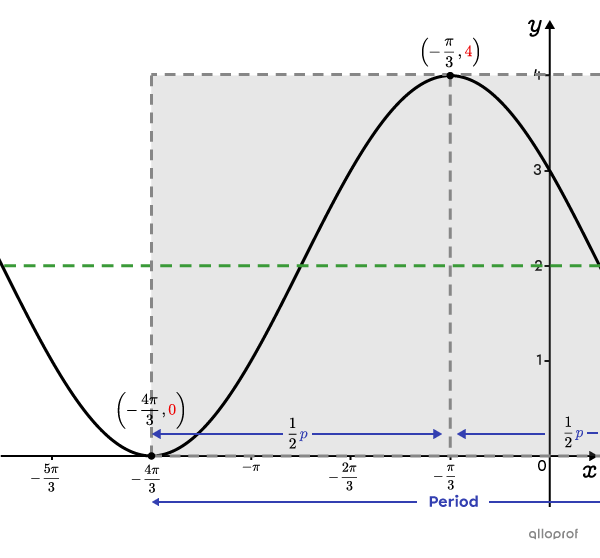
Sketch a rectangle framing one cycle starting at point |\left(-\dfrac{4\pi}{3},0\right).| In this example, the function's cycle is not completely shown. For a cycle to be complete, it must end at the same height as the selected extreme, which in this case is a minimum. -
Determine |\vert a\vert| from the amplitude.
The absolute value of |a| is determined from the amplitude.||\begin{align}\vert a\vert&=\color{#fa7921}A\\&=\dfrac{\max-\min}{2}\\&=\dfrac{\color{#EC0000}{4}-\color{#EC0000}{0}}{2}\\&=\color{#fa7921}{2}\end{align}||

-
Determine |b| from the period.
The value of |b| is found using the period.
There is a half-period between a maximum and a minimum. To calculate the full period, proceed as follows:||\begin{align}\dfrac{1}{2}\color{#333fb1}p&=\color{#333fb1}{-\dfrac{\pi}{3}}-\color{#333fb1}{-\dfrac{4\pi}{3}}\\\dfrac{1}{2}\color{#333fb1}p&=\dfrac{3\pi}{3}\\\dfrac{1}{2}\color{#333fb1}p&=\pi\\\color{#333fb1}p&=\color{#333fb1}{2\pi}\end{align}||Now, we can determine |b.|||\begin{align}\color{#333fb1}p&=\dfrac{2\pi}{\vert b\vert}\\\color{#333fb1}{2\pi}&=\dfrac{2\pi}{\vert b\vert}\quad\Leftrightarrow&\vert b\vert&=\dfrac{2\pi}{2\pi}\\&&\vert b\vert&=1\\&&b&=1\end{align}||
-
Determine the sign of |a.|
Since the starting point of the cycle is a minimum, |a| is negative.||a<0|| -
Write the rule of the function.
The rule of the cosine function is |f(x)=-2\cos\left(x+\dfrac{4\pi}{3}\right)+2.|
Here is an example where the vertices are not directly provided. This requires a little more calculation to determine the parameters.
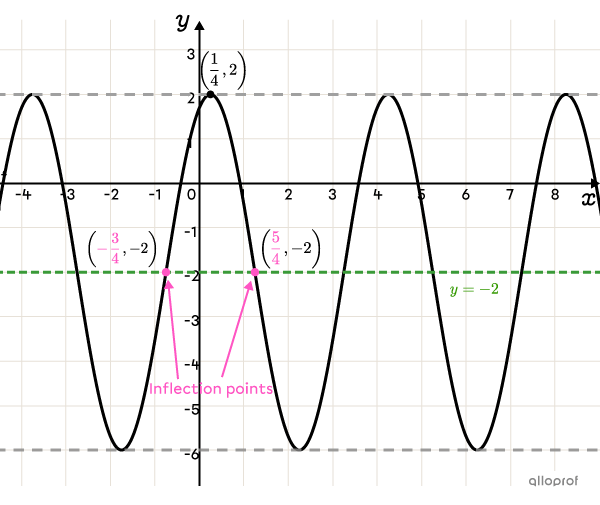
Determine the rule of the cosine function that passes through points |\left(-\dfrac{3}{4},-2\right)| and |\left(\dfrac{5}{4},-2\right).|

-
Determine |k| using the axis of oscillation.
To determine the value of |k,| use the following formula:||k=\dfrac{\max+\min}{2}||The coordinates of the maximum and minimum are not given, but they can be deduced from the graph. We can see that the function has a maximum at |2| and a minimum at |-6.|||\begin{align}k&=\dfrac{\max+\min}{2}\\&=\dfrac{\color{#EC0000}{2}+\color{#EC0000}{-6}}{2}\\&=-2\end{align}||
-
Choose an extreme point and determine |h.|
Since |k=-2,| the points provided are inflection points, that is, points located on the axis of oscillation. Since there is a maximum exactly between these 2 points, we can deduce the value of |h| as follows:||\begin{align}h&=\dfrac{\color{#FF55C3}{-\frac{3}{4}}+\color{#FF55C3}{\frac{5}{4}}}{2}\\&=\dfrac{1}{4}\end{align}||The maximum located between the 2 given points is point |\left(\dfrac{1}{4},2\right).|||h=\dfrac{1}{4}||
-
Determine one cycle starting from the chosen extreme.
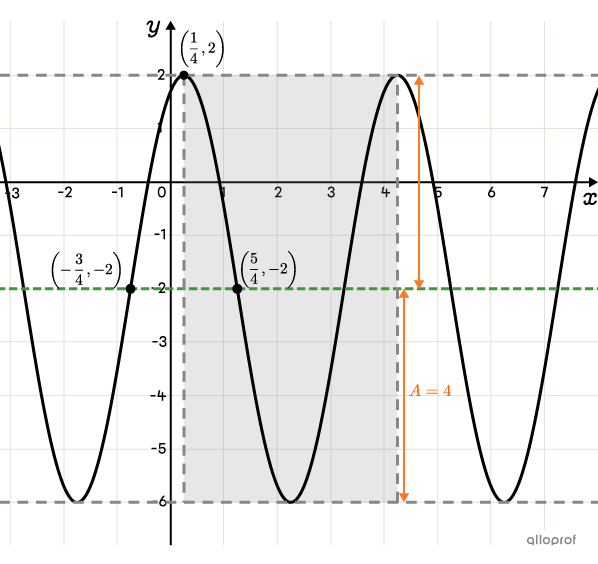
Sketch a rectangle framing one cycle starting at point |\left(\dfrac{1}{4},2\right).| -
Determine |\vert a\vert| from the amplitude.
The absolute value of |a| is determined from the amplitude.||\begin{align}\vert a\vert&=\color{#fa7921}A\\&=\dfrac{\max-\min}{2}\\&=\dfrac{\color{#EC0000}{2}-\color{#EC0000}{-6}}{2}\\&=\color{#fa7921}{4}\end{align}||
-
Determine |b| from the period.
The value of |b| is found using the period.
There is a quarter-period between the maximum and point |\left(\dfrac{5}{4},-2\right).| To calculate the full period, proceed as follows:||\begin{align}\dfrac{1}{4}\color{#333fb1}p&=\color{#333fb1}{\dfrac{5}{4}}-\color{#333fb1}{\dfrac{1}{4}}\\\dfrac{1}{4}\color{#333fb1}p&=1\\\color{#333fb1}p&=\color{#333fb1}4\end{align}||Now, we can determine |b.|||\begin{align}\color{#333fb1}p&=\dfrac{2\pi}{\vert b\vert}\\\color{#333fb1}{4}&=\dfrac{2\pi}{\vert b\vert}\quad\Leftrightarrow&\vert b\vert&=\dfrac{2\pi}{4}\\&&\vert b\vert&=\dfrac{\pi}{2}\\&&b&=\dfrac{\pi}{2}\end{align}||
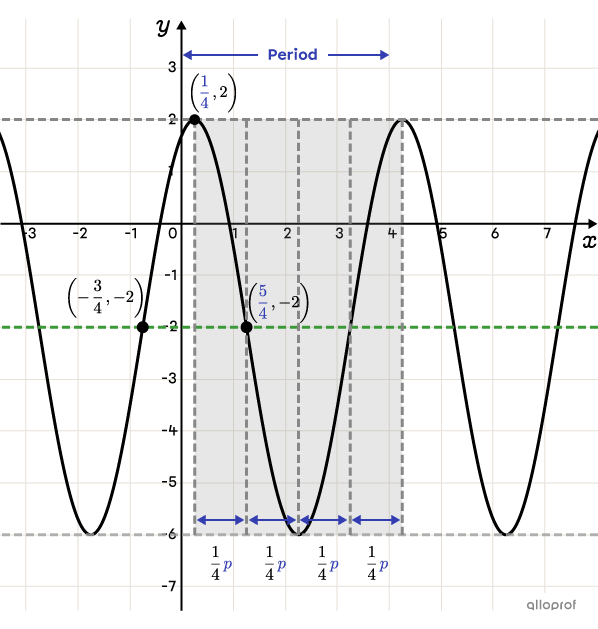
-
Determine the sign of |a.|
Since the starting point of the cycle is a maximum, |a| is positive.||a>0|| -
Write the rule of the function.
The rule of the cosine function is |f(x)=4\cos\!\Bigg(\dfrac{\pi}{2}\left(x-\dfrac{1}{4}\right)\!\Bigg)-2.|
When the inflection points of a sinusoidal function are given, it is best to find the rule of a sine function. That way, there are fewer calculations.
When asked to find the equation of a sinusoidal function, it's possible to use the equation of a sine function or a cosine function. Here is an example of how to find the equation of a cosine function using trigonometric identities.
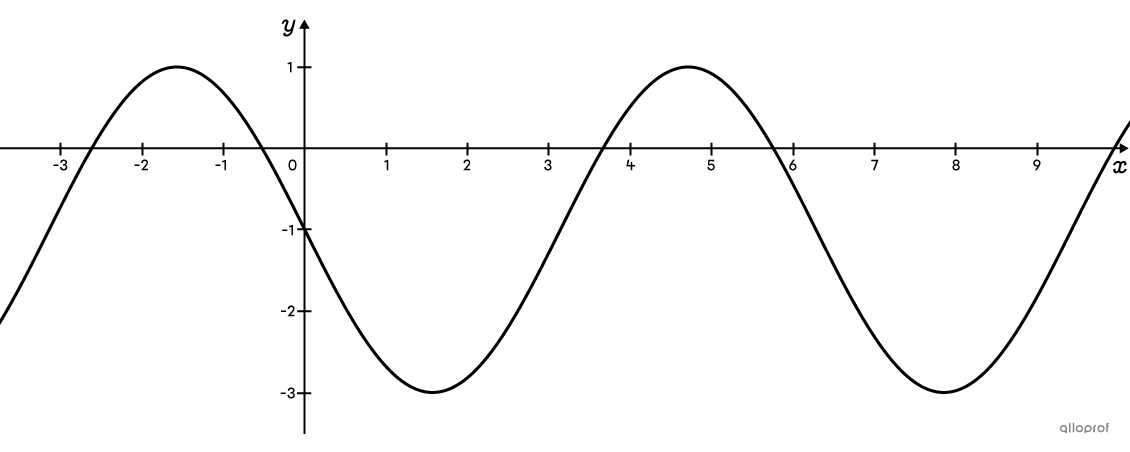
Here is a sinusoidal function whose rule, based on the sine function, is |f(x)=-2\sin(x)-1.|
To transform the equation into a cosine function, apply the following trigonometric identity:
|\sin(x)=\color{#3A9A38}{\cos}\left(x\color{#3A9A38}{-\dfrac{\pi}{2}}\right).|||\begin{align}f(x)&=-2\sin(x)-1\\ f(x)&=-2\color{#3A9A38}{\cos}\left(x\color{#3A9A38}{-\dfrac{\pi}{2}}\right)-1\end{align}||The 2 previous rules are equivalent.
Note: Although the rule changed from a sine function to a cosine function, |\vert a \vert| and |\vert b\vert| did not change, since the amplitude and the period remained the same. Notice that |k| did not change either, since the axis of oscillation is also the same.
The only possible differences between the rules are the value of |h,| and the signs of |a| and |b.|