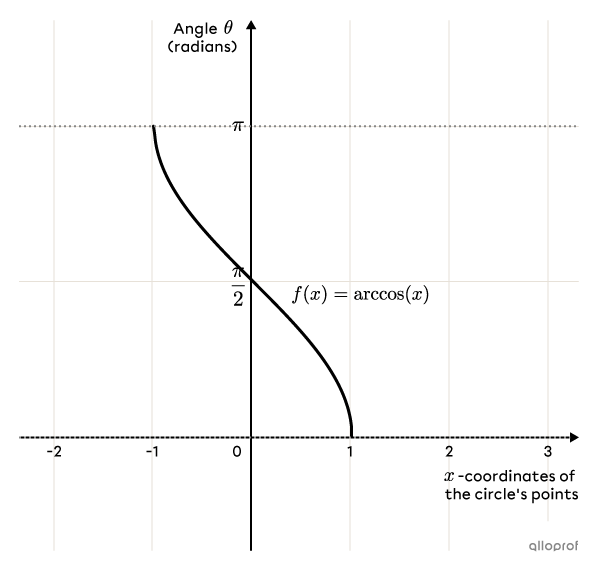
The inverse of the basic cosine function is the arc cosine function, which maps the measure of the angles (in radians) on the unit circle as a function of the |x|-coordinates of the points on the circle.
The rule for the basic arc cosine function is |f(x)=\arccos (x).| This function is also denoted |f(x)=\cos^{-1}(x).|
Note: The notation |\cos^{-1}(x)| should not be confused with |\dfrac{1}{\cos (x)}.|
Here is a summary of the properties of the |\arccos| function.
-
The domain of the function is |[-1,1].|
-
The range (codomain) is |[0, \pi].|
-
The |y|-intercept is |\dfrac{\pi}{2}.|
-
The |x|-intercept is |1.|
-
The function is decreasing over its domain.
-
The function is positive over its domain.
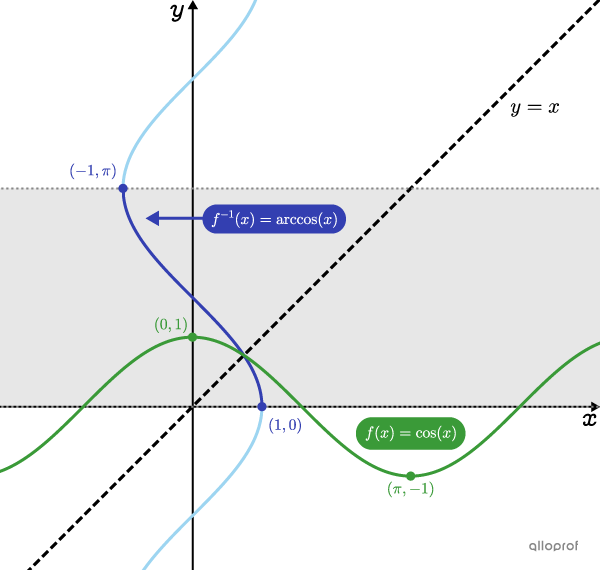
The inverse of a cosine function is not a function. In order for it to become one, we must restrict its range.
In the Cartesian plane below, we have sketched the basic cosine function. To graph its inverse, interchange the coordinates |x| and |y| of the points of the function. Another method to achieve this, is to reflect the points with respect to the line of equation |y=x.| For example, the point |(0,1)| becomes the point |(1,0).|
By doing so, we obtain another curve, which is not a function. By restricting the range of the inverse to the interval |[0, \pi],| we obtain the arc cosine function.
To find the rule of the inverse of a cosine function, follow these steps.
-
Interchange |x| and |y| in the rule.
-
Isolate the variable |y.|
-
Write the rule of the inverse.
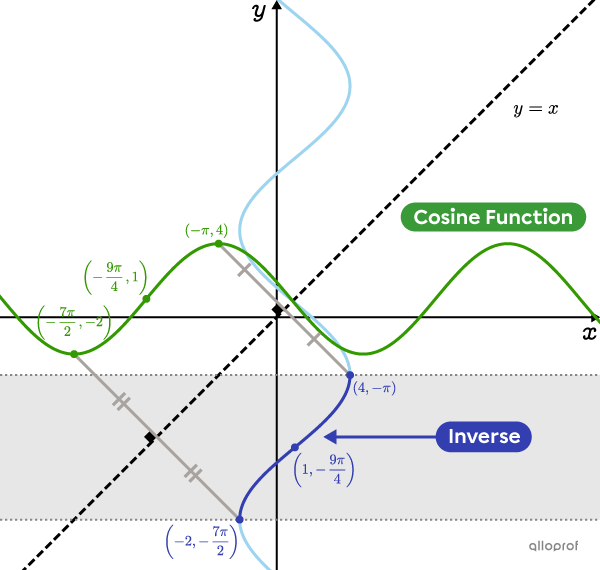
Find the rule of the inverse of the function |f(x)=3\cos\left(-\dfrac{2}{5}(x+\pi)\right)+1.|
-
Interchange |x| and |y| in the rule ||\begin{align}\color{#3B87CD}y&=3\cos\left(-\dfrac{2}{5}(\color{#FF55C3}x+\pi)\right)+1\\ \color{#FF55C3}x&=3\cos\left(-\dfrac{2}{5}(\color{#3B87CD}y+\pi)\right)+1\end{align}||
-
Isolate the variable |y|
||\begin{align}x&=3\cos\left(-\dfrac{2}{5}(\color{#3B87CD}y+\pi)\right)+1\\x-1&=3\cos\left(-\dfrac{2}{5}(\color{#3B87CD}y+\pi)\right)\\ \dfrac{x-1}{3}&=\cos\left(-\dfrac{2}{5}(\color{#3B87CD}y+\pi)\right)\end{align}||To isolate |y,| it is necessary to eliminate |\cos| by performing the inverse operation, |\cos^{-1}.|
||\begin{align}\color{#EC0000}{\cos^{-1}\!\left(\color{black}{\dfrac{x-1}{3}}\right)}&=-\dfrac{2}{5}(\color{#3B87CD}y+\pi)\\-\dfrac{5}{2}\cos^{-1}\!\left(\dfrac{x-1}{3}\right)&=\color{#3B87CD}y+\pi\\
-\dfrac{5}{2}\cos^{-1}\!\left(\dfrac{x-1}{3}\right)-\pi&=\color{#3B87CD}y\end{align}||
It is possible to simplify the writing by working inside the brackets. In fact, division by |3| can also be written as multiplication by |\dfrac{1}{3}.|||\begin{align}-\dfrac{5}{2}\cos^{-1}\!\left(\color{#EC0000}{\dfrac{x-1}{3}}\right)-\pi&=y\\ -\dfrac{5}{2}\cos^{-1}\!\left(\color{#EC0000}{\dfrac{1}{3}(x-1)}\right)-\pi&=y\end{align}||
-
Write the rule of the inverse
The rule of the inverse of the cosine function is as follows.
||f^{-1}(x)=-\dfrac{5}{2}\cos^{-1}\!\left(\dfrac{1}{3}(x-1)\right)-\pi||
Note: In order for the inverse to become a function, we must restrict its range.
Here is the graphical representation of the cosine function from the previous example, whose rule is |f(x)=3\cos\left(-\dfrac{2}{5}(x+\pi)\right)+1.|
In order for the inverse to become a function, we restrict its range. In this example, we must restrict its range to the interval |\color{#333fb1}{\left[-\dfrac{7\pi}{2},-\pi\right]}.|