Une fraction est irréductible lorsque le numérateur et le dénominateur ont seulement |1| comme diviseur commun. La fraction est alors réduite à sa plus simple expression.
Une fraction est réduite en divisant le numérateur et le dénominateur par un même nombre.
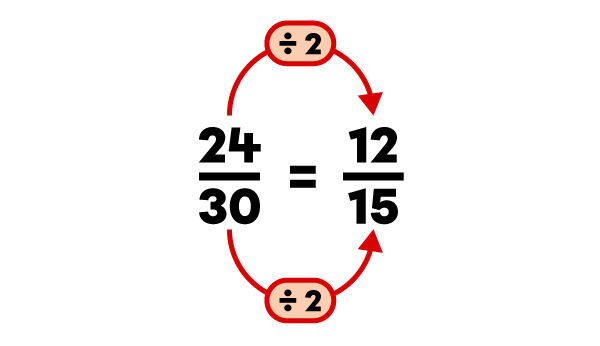
La fraction obtenue peut parfois être réduite de nouveau.
Dans cet exemple, la fraction |\dfrac{12}{15}| peut être réduite de nouveau.
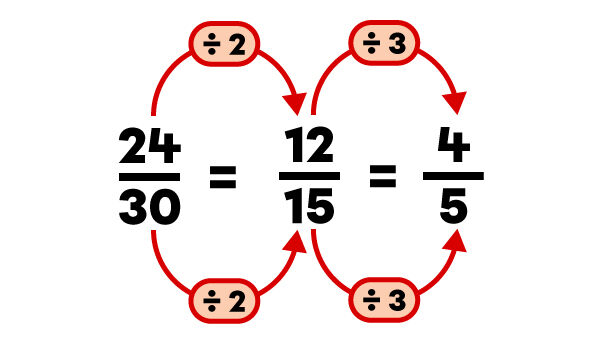
C’est lorsqu’il n’existe plus de diviseur commun entre le numérateur et le dénominateur que la fraction est irréductible.
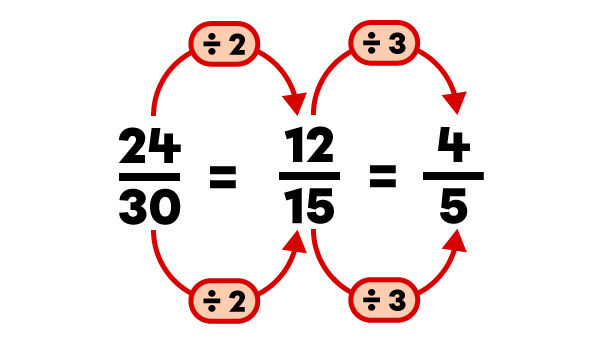
Ici, |4| et |5| ont seulement |1| comme diviseur commun. La fraction irréductible est |\dfrac{4}{5}| puisque |4| divisé par |1| égale |4| et que |5| divisé par |1| égale |5|. Elle est donc réduite à sa plus simple expression.
Une fraction réduite ou irréductible doit toujours être équivalente à la fraction initiale.
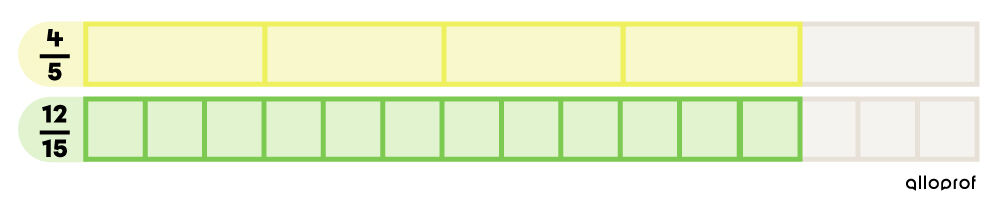
-
Je trouve un diviseur commun au numérateur et au dénominateur.
-
Je divise le numérateur par ce nombre.
-
Je divise le dénominateur par ce nombre.
-
Je recommence les étapes |1|, |2| et |3| jusqu’à ce qu’il n’y ait plus de diviseur commun autre que |1|.
Quelle est la fraction irréductible de |\dfrac{36}{48}|?
|
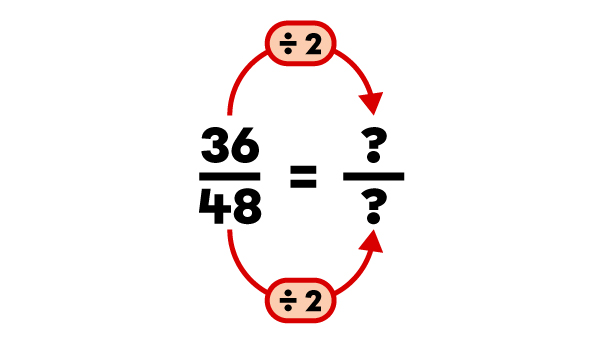
|
|
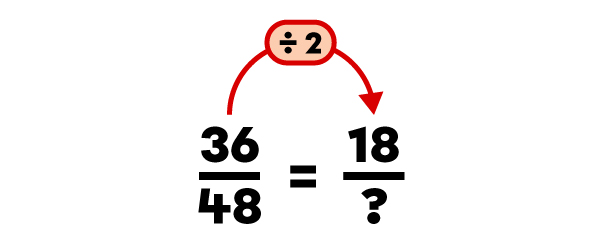
|
|
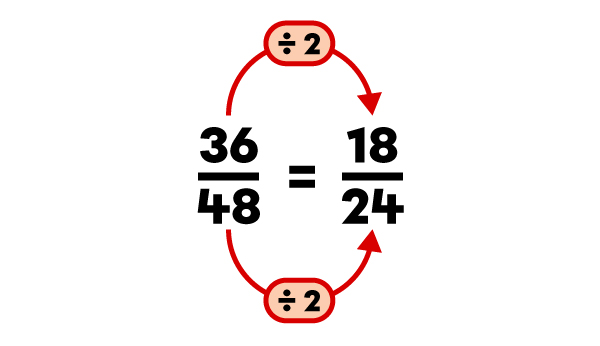
|
|
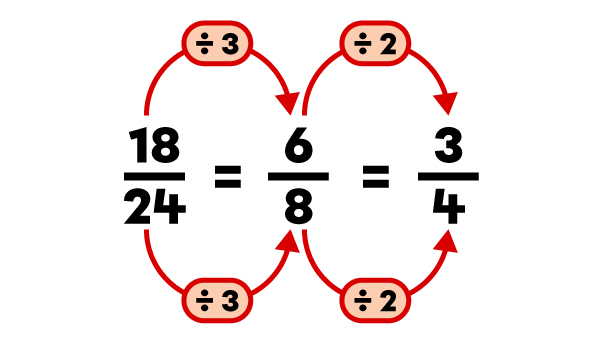
|
La fraction |\dfrac{3}{4}| est la fraction irréductible de |\dfrac{36}{48}|.
-
Je trouve le PGCD du numérateur et du dénominateur.
-
Je divise le numérateur par ce nombre.
-
Je divise le dénominateur par ce nombre.
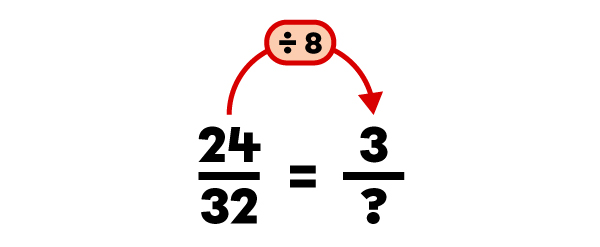
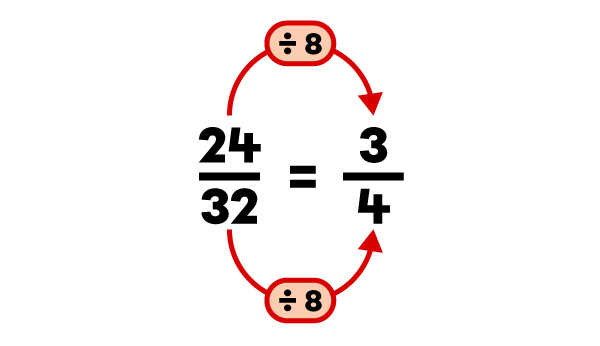
Quelle est la fraction irréductible de |\dfrac{24}{32}|?
|
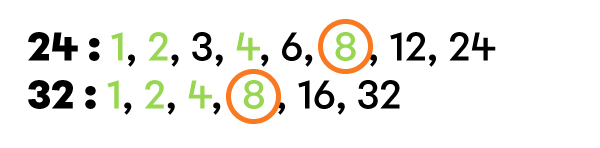
|
|
|
|
|
La fraction |\dfrac{3}{4}| est la fraction irréductible de |\dfrac{24}{32}|.