In a right triangle, if the height |(\boldsymbol{h})| is drawn from the right angle, 2 new right triangles are created. We can prove that these 3 triangles are similar to each other using the minimum condition A-A.
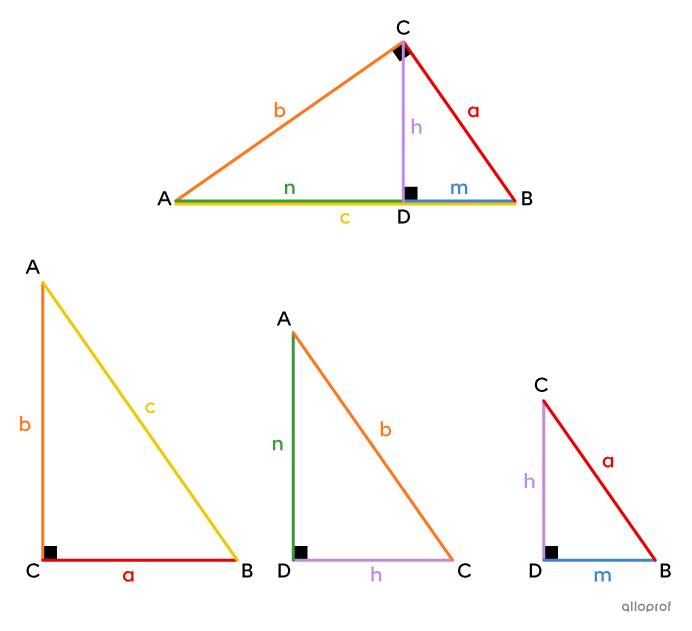
It is possible to create several proportions from the corresponding sides of these right triangles. These proportions yield 3 metric relations that can be used to find missing measurements in right triangles.
||\begin{align}\dfrac{\color{#3b87cd}m}{\color{#ec0000}a}&=\dfrac{\color{#EC0000}a}{\color{#efc807}c}\\\\
\dfrac{\color{#3a9a38}n}{\color{#fa7921}b}&=\dfrac{\color{#fa7921}b}{\color{#efc807}c}\end{align}||
Altitude to Hypotenuse Theorem
||\dfrac{\color{#3b87cd}m}{\color{#c58ae1}h}=\dfrac{\color{#c58ae1}h}{\color{#3a9a38}n}||
||\dfrac{\color{#c58ae1}h}{\color{#ec0000}a}=\dfrac{\color{#fa7921}b}{\color{#efc807}c}||
Here are the steps to find the length of a segment in a triangle using metric relations.
-
Identify the given measurements and the unknown measurement.
-
Determine which metric relation to use.
-
Find the missing measurement.
If more than one measure is missing in order for a metric relation to be used, one can sometimes be found using the Pythagorean theorem.
In a right triangle, each leg |(a| and |b)| is the proportional mean between its projection onto the hypotenuse |(m| or |n)| and the entire hypotenuse |(c).|
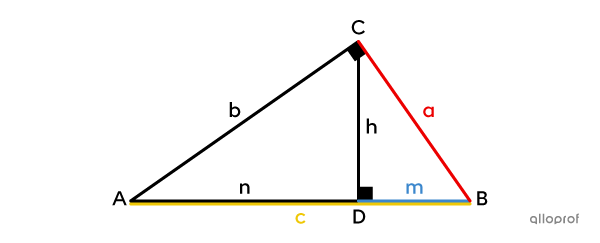
|\dfrac{\color{#3b87cd}m}{\color{#ec0000}a}=\dfrac{\color{#ec0000}a}{\color{#efc807}c}\ \Rightarrow\ \color{#ec0000}a^2= \color{#3b87cd}m\color{#efc807}c|
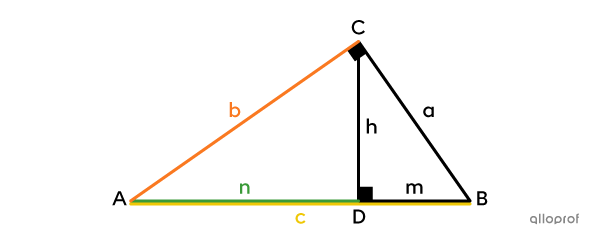
|\dfrac{\color{#3a9a38}n}{\color{#fa7921}b}=\dfrac{\color{#fa7921}b}{\color{#efc807}c}\ \Rightarrow\ \color{#fa7921}b^2=\color{#3a9a38}n\color{#efc807}c|
Determine the measure of |\overline{BC}| in the following triangle.

-
Identify the given measurements and the unknown measurement.
||\begin{align}\text{m}\overline{AB}&=c=16\ \text{cm}\\\text{m}\overline{BD}&=m=4\ \text{cm}\\\text{m}\overline{BC}&=a=\ ?\end{align}|| -
Determine which metric relation to use.
We are looking for the metric relation that involves measurements |a,| |c| and |m.| This is the Proportional Mean theorem. -
Find the missing measurement.
||\begin{align}a^2 &= m c \\a^2 &= 4\times 16\\a^2 &= 64\\a &= 8\end{align}||
Answer: Segment |\overline{BC}| measures |8\ \text{cm}.|
In a right triangle, the height |(h)| drawn from the right angle is the proportional mean between the 2 segments it creates on the hypotenuse |(m| and |n).|
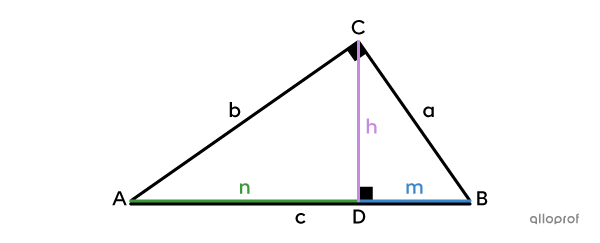
|\dfrac{\color{#3b87cd}m}{\color{#c58ae1}h}=\dfrac{\color{#c58ae1}h}{\color{#3a9a38}n}\ \Rightarrow\ \color{#c58ae1}h^2 = \color{#3b87cd}m\color{#3a9a38}n|
Find the measure of |\overline{BD}| in the following triangle.

-
Identify the given measurements and the unknown measurement.
||\begin{align}\text{m}\overline{AD}&=n=12\ \text{cm}\\
\text{m}\overline{CD}&=h=6\ \text{cm}\\
\text{m}\overline{BD}&=m=\ ?\end{align}|| -
Determine which metric relation to use.
We are looking for the metric relation that involves measurements |h,| |m| and |n.| This is the Altitude to Hypotenuse theorem. -
Find the missing measurement.
||\begin{align}h^2 &= mn\\6^2 &= 12\times m\\36 &= 12\times m\\3 &= m\end{align}||
Answer: Segment |\overline{BD}| measures |3\ \text{cm}.|
In a right triangle, the product of hypotenuse |(c)| and the corresponding height |(h)| is equal to the product of the legs |(a| and |b).|
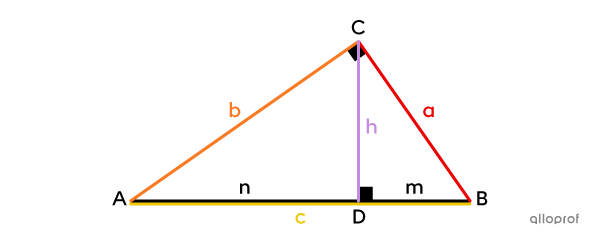
|\dfrac{\color{#c58ae1}h}{\color{#ec0000}a}=\dfrac{\color{#fa7921}b}{\color{#efc807}c}\ \Rightarrow\ \color{#efc807}c\color{#c58ae1}h = \color{#ec0000}a\color{#fa7921}b|
Find the measure of |\overline{CD}| in the following triangle.
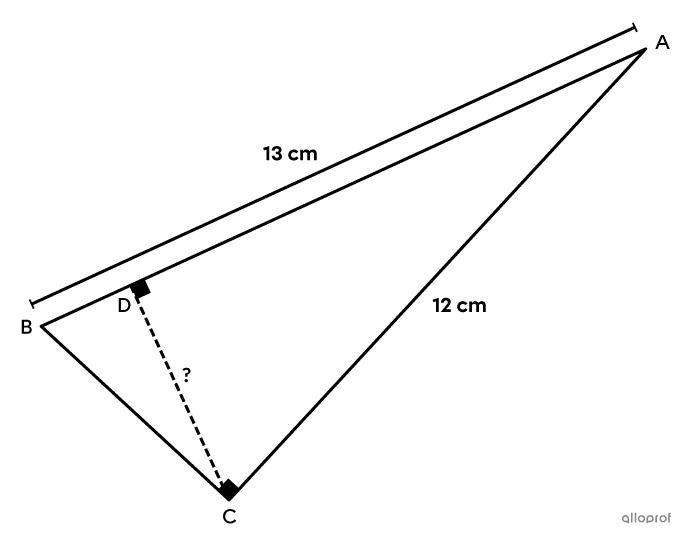
-
Identify the given measurements and the unknown measurement.
||\begin{align}\text{m}\overline{AB}&=c=13\ \text{cm}\\
\text{m}\overline{AC}&=b=12\ \text{cm}\\
\text{m}\overline{CD}&=h=\ ?\end{align}|| -
Determine which metric relation to use.No metric relation uses only these 3 values. However, if we use the Product of the Sides theorem, only the length of the second leg is missing |(\overline{BC}),| and it can be found using the Pythagorean theorem.||\begin{align} a^2 + b^2 &= c^2\\a^2 + 12^2 &= 13^2\\a^2 &= 169 - 144\\a^2 &= 25\\a &= 5\end{align}||
-
Find the missing measurement.
||\begin{align}ch&=ab\\13h &= 5\times 12\\13h &= 60\\h &\approx 4.6\end{align}||
Answer: Segment |\overline{CD}| measures approximately |4.6\ \text{cm}.|
More complex problems can be solved by using multiple metric relations.
In the image below, segment |\overline{BC}| measures |100\ \text{cm},| and segment |\overline{AC}| measures |116.62\ \text{cm}.| Find the length of segment |\overline{DE}.|
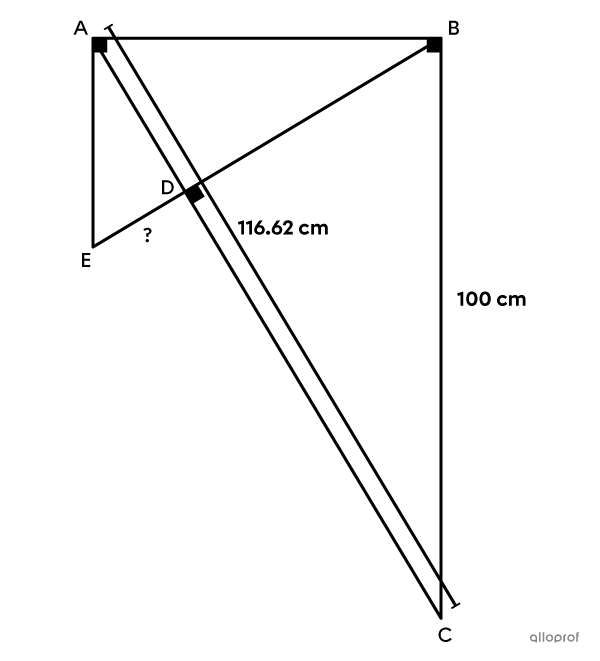
The image consists of 2 right triangles onto which metric relations can be applied: |\triangle ABC| and |\triangle ABE.| The measurement sought is part of |\triangle ABE,| but none of its other measurements were provided. Start by finding the measures of |\triangle ABC.| Since the length of the hypotenuse and of one of the legs is given, the length of the second leg can be found using the Pythagorean theorem.||\begin{align}\left(\text{m}\overline{AC}\right)^2&=\left(\text{m}\overline{AB}\right)^2+\left(\text{m}\overline{BC}\right)^2\\
116.62^2&=\left(\text{m}\overline{AB}\right)^2+100^2\\
13\ 600.22&\approx\left(\text{m}\overline{AB}\right)^2+10\ 000\\
3600.22&\approx\left(\text{m}\overline{AB}\right)^2\\
60&\approx\text{m}\overline{AB}
\end{align}||We now have one of the measurements of |\triangle ABE,| but one is not enough. By applying the Product of the Sides theorem to |\triangle ABC|, we can find the length of |\overline{BD}.|||\begin{align}\color{#efc807}{\text{m}\overline{AC}}\times\color{#c58ae1}{\text{m}\overline{BD}}&=\color{#ec0000}{\text{m}\overline{AB}}\times \color{#fa7921}{\text{m}\overline{BC}}\\
116.62\times\text{m}\overline{BD}&=60\times 100\\
116.62\times\text{m}\overline{BD}&=6\ 000\\
\text{m}\overline{BD}&\approx51.45
\end{align}||The measures of |\triangle ABE| can now be found. Having obtained the length of one of the legs and its projection onto the hypotenuse, we can use the Proportional Mean theorem to find the length of the hypotenuse of |\triangle ABE.|||\begin{align}\left(\color{#fa7921}{\text{m}\overline{AB}}\right)^2&=\color{#3a9a38}{\text{m}\overline{BD}}\times \color{#efc807}{\text{m}\overline{BE}}\\
60^2&=51.45\times \text{m}\overline{BE}\\
3600&=51.45\times \text{m}\overline{BE}\\
69.97&\approx\text{m}\overline{BE}
\end{align}||All that is left to do is subtract to find the measurement sought.||\begin{align}\text{m}\overline{DE}&=\text{m}\overline{BE}- \text{m}\overline{BD}\\
\text{m}\overline{DE}&=69.97- 51.45\\
\text{m}\overline{DE}&=18.52\ \text{cm}
\end{align}||Answer: Segment |\overline{DE}| measures |18.52\ \text{cm}.|
Pour valider ta compréhension à propos des démonstrations de façon interactive, consulte la MiniRécup suivante.
