When comparing 2 plane figures, it is possible to check if they are congruent (isometric) or similar by analyzing if their corresponding sides are the result of the same geometric transformations.
-
Corresponding sides are the same sides in different figures.
-
Corresponding angles are the same angles in different figures.
When comparing 2 plane figures, we might assume that all the corresponding sides or angles are congruent or proportional. However, as the following two pairs of triangles show, it is not the case.
The sides |\color{#333fb1}{\overline{BC}}| and |\color{#333fb1}{\overline{JK}}| are corresponding, since they are both the longest side (the hypotenuse) of their respective triangle.
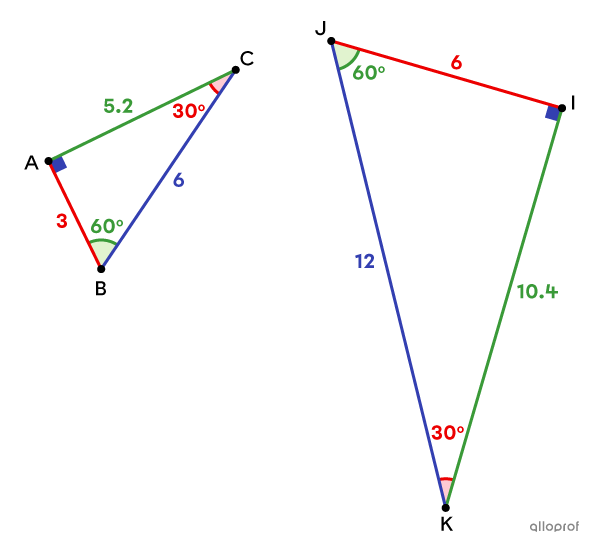
|\Delta ABC| and |\Delta IJK| are similar, because all corresponding angles are congruent.
Therefore, all the corresponding sides are proportional.
The sides |\color{#333fb1}{\overline{BC}}| and |\color{#333fb1}{\overline{ST}}| are corresponding, since they are both the longest side (the hypotenuse) of their respective triangle.
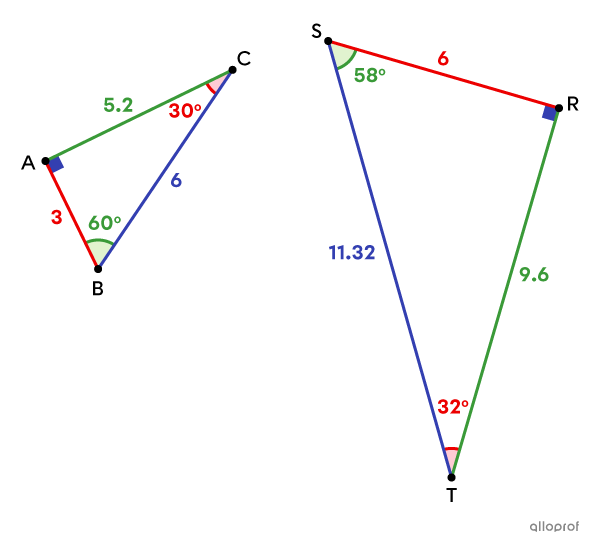
|\Delta ABC| and |\Delta RST| are not similar, since some of the corresponding angles are not congruent.
Therefore, the corresponding sides are not proportional.
The word isometry originates from ancient Greek. The word is a combination of iso, meaning same, and metron, meaning measure. We often use the word congruency to refer to isometry.
Two plane figures are considered congruent (or isometric) if all their corresponding sides and angles are congruent.
To determine whether two figures are congruent, we only need to show that one of them (the image figure) is the result of one or more geometric transformations applied to the other figure (the initial figure). The geometric transformations are listed below.
It is also possible to show that 2 figures are congruent in a different way, without using geometric transformations. In fact, if all the corresponding sides are congruent, then it is enough evidence to state that the two figures are congruent.
In the following interactive animation, you can move the Translation, Rotation, and Reflection sliders to show the congruency (isometry) of the 4 regular pentagons.
--
The following is an example where several geometric transformations are needed to prove 2 figures are congruent.
Using the Translation and Rotation sliders in the following interactive animation, find the translation distance and angle of rotation proving the orange trapezoid is congruent to the red trapezoid.
Notice the red trapezoid perfectly overlaps the orange trapezoid if a translation of |12| units followed by a rotation of |100^\circ| regarding the point |O| is applied. It implies that all corresponding sides and all corresponding angles are congruent. Therefore, we can conclude the 2 trapezoids are congruent.
Congruent figures are necessarily equivalent figures.
However, equivalent figures are not necessarily congruent figures.
Two figures are called similar if all the ratios of their corresponding sides are proportional and all their corresponding angles are congruent.
To determine if two figures are similar, we must prove that one of them (the image figure) is the result of a dilation (homothety) of the other (the initial figure).
It is also possible to show two figures are similar in a different manner. In fact, if the quotients of all the corresponding sides are equal, it is enough to conclude that the two figures are similar.
The value of the quotients of the corresponding sides is a ratio denoted |k.| The value is the similarity ratio (scale factor) of the two similar figures. Without taking into account the sign, the scale factor is equivalent to the similarity ratio.
In the following interactive animation, you can move the Dilation Scale Factor slider to show the 3 triangles are similar with respect to the centre of dilation.
When the scale factor is |2,| each side of the blue triangle is twice as long as the corresponding side of the purple triangle. When the scale factor is |0.5,| each side of the green triangle is half the size of the corresponding side of the purple triangle.
The corresponding angles are all congruent, regardless of the scale factor's value.
Sometimes a dilation is not sufficient to prove similarity; therefore, a translation, rotation, and/or reflection is needed.
In the following example, we have to find a missing measure knowing the two figures are similar.
Find the measure of the side |\overline{YZ}| knowing that rectangle |\color{#3a9a38}{ABCD}| is similar to rectangle |\color{#333fb1}{WXYZ}.|
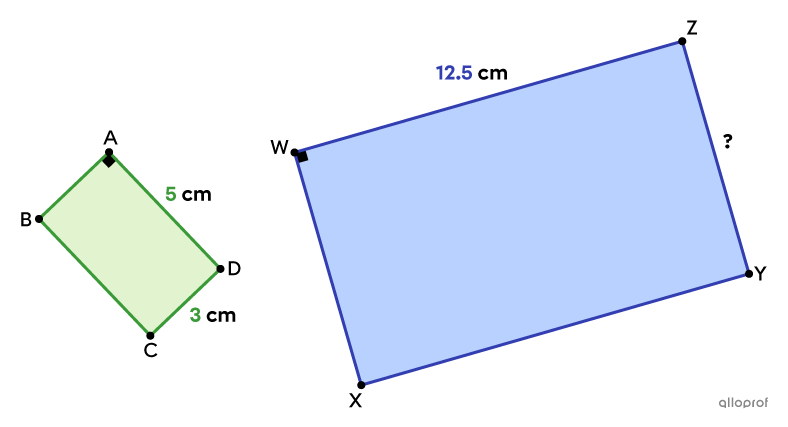
Because the 2 rectangles are similar, we can find a proportion using the ratios of the corresponding sides.
We see that sides |\color{#3a9a38}{\overline{DA}}| and |\color{#333fb1}{\overline{ZW}}| are corresponding, since they are both the longest sides of their respective rectangle. Likewise, sides |\color{#3a9a38}{\overline{CD}}| and |\color{#333fb1}{\overline{YZ}}| are corresponding because they are both the shortest sides of their respective rectangle.
Therefore, we have the following proportion.
||\begin{align}\dfrac{\color{#3a9a38}{\text{m}\overline{DA}}}{\color{#333fb1}{\text{m}\overline{ZW}}}&=\dfrac{\color{#3a9a38}{\text{m}\overline{CD}}}{\color{#333fb1}{\text{m}\overline{YZ}}}\\\\\dfrac{\color{#3a9a38}{5\ \text{cm}}}{\color{#333fb1}{12.5\ \text{cm}}}&=\dfrac{\color{#3a9a38}{3\ \text{cm}}}{\color{#333fb1}{\text{m}\overline{YZ}}}\end{align}||
Next, use cross-multiplication to eliminate the fractions.
||\begin{align}\dfrac{5\ \text{cm}}{12.5\ \text{cm}}&=\dfrac{3\ \text{cm}}{\text{m}\overline{YZ}}\\\\\text{m}\overline{YZ}\times5\ \text{cm}&=3\ \text{cm}\times12.5\ \text{cm}\end{align}||
Finally, isolate |\text{m}\overline{YZ}| using the balancing equations method.
||\begin{align}\color{#ec0000}{\dfrac{\color{black}{\text{m}\overline{YZ}\times\color{#ec0000}{\cancel{\color{black}{5\ \text{cm}}}}}}{\cancel{5\ \text{cm}}}}&=\color{#ec0000}{\dfrac{\color{black}{3\ \text{cm}\times12.5\ \text{cm}}}{5\ \text{cm}}}\\\\\text{m}\overline{YZ}&=7.5\ \text{cm}\end{align}||
Answer: The measure of side |\overline{YZ}| is |7.5\ \text{cm}.|