When comparing polygons, we can determine if they are similar figures by checking if they have corresponding congruent angles and proportional sides. The same is true for triangles. To prove the similarity of triangles, it is not necessary to know the measure of all sides and angles. It is enough to verify that certain minimum conditions are respected. This is called the minimum conditions for similar triangles.
The minimum conditions for similar triangles make it possible to prove that triangles are similar using the fewest arguments possible.
There are 3 cases of similarity in triangles. There are also cases of isometry (congruence) of triangles. We use the most appropriate one according to the information provided in the problem and we organize the process in a table of statements and justifications.
We can explain why the minimum conditions are sufficient to assert that triangles are similar by looking at the constructions of the triangles in question.
In the interactive animation below, you may select one of the minimum conditions for similarity, then drag the cursor to the right to see an explanation of the construction of similar triangles.
Triangles are similar if and only if their corresponding sides are proportional.
The condition SSS (Side-Side-Side) does not involve any angle measures. To conclude that the triangles are similar, it is enough to show that the 3 ratios of the corresponding sides are equivalent.
Prove that triangles |ABC| and |EFG| are similar.

| Statement | Justification | ||
|---|---|---|---|
|
1 |
The corresponding sides are proportional. |
S |
|\dfrac{\text{m}\overline{AB}}{\text{m}\overline{EF}}=\dfrac{2.72}{1.36}=2| |
|
S |
|\dfrac{\text{m}\overline{AC}}{\text{m}\overline{EG}}=\dfrac{4.8}{2.4}=2| |
||
|
S |
|\dfrac{\text{m}\overline{BC}}{\text{m}\overline{FG}}=\dfrac{3.96}{1.98}=2| |
||
|
2 |
Triangles |ABC| and |EFG| are similar. ||\triangle ABC\sim\triangle EFG|| |
They satisfy the minimum condition SSS: triangles are similar if their corresponding sides are proportional. |
|
Triangles are similar if and only if they have one pair of congruent angles situated between two pairs of proportional corresponding sides.
The SAS (Side-Angle-Side) condition requires that the pair of congruent angles must be located between the proportional sides. In other words, the order of the letters (SAS) is important.
Prove that triangles |ADC| and |CDB| in the following figure are similar.
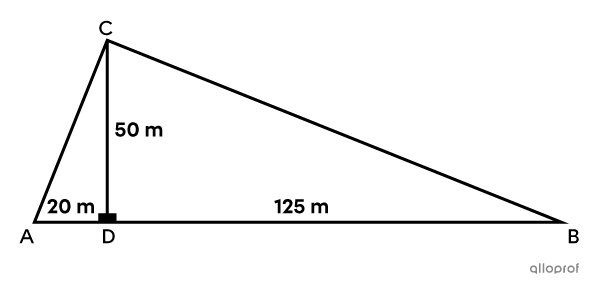
Before completing the statement and justification table, it is important to identify the corresponding sides and angles. To help, you can arrange the triangles |ADC| and |CDB| in the same way, like this:
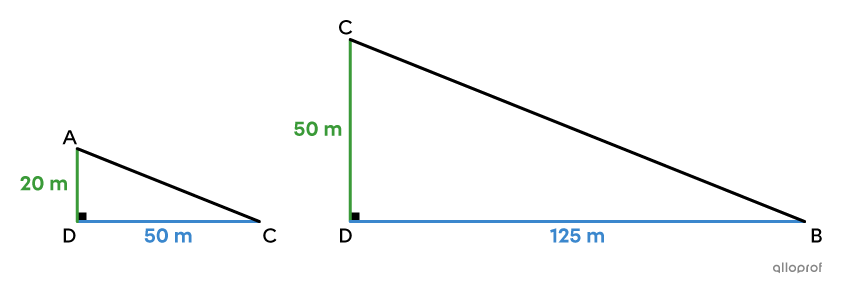
The pairs of corresponding segments whose measures are known are |\color{#3a9a38}{\overline{AD}}| and |\color{#3a9a38}{\overline{CD}},| as well as |\color{#3b87cd}{\overline{CD}}| and |\color{#3b87cd}{\overline{BD}}.|
The pair of known corresponding angles is angle ADC and angle CDB. In addition, for each of the triangles, we must make sure that the angle we know is actually located between the 2 given segments.
| Statement | Justification | ||
|---|---|---|---|
|
1 |
There are 2 pairs of corresponding proportional sides. |
S |
|\dfrac{\text{m}\overline{CD}}{\text{m}\overline{AD}}=\dfrac{50}{20}=2.5| |
|
S |
|\dfrac{\text{m}\overline{BD}}{\text{m}\overline{CD}}=\dfrac{125}{50}=2.5| |
||
|
2 |
Corresponding angles |ADC| and |CDB| are congruent. ||\angle ADC\cong\angle CDB|| |
A |
By hypothesis. The information is given in the figure: |\text{m}\angle ADC=\text{m}\angle CDB=90^\circ.| |
|
3 |
Triangles |ABC| and |CDB| are similar. ||\triangle ABC\sim\triangle CDB|| |
They satisfy the minimum condition SAS: triangles are similar if they have one pair of congruent angles situated between 2 pairs of proportional corresponding sides. |
|
Note: The figure shown in this example may bring to mind the metric relationships in the right triangle. However, one cannot use them to find missing measures unless one first proves that triangle |ABC| is right-angled at |C,| which is not shown in the figure.
The selected angle must be formed by the pairs of corresponding sides analyzed. If the angle is not in the correct place, the 2 triangles are not necessarily similar.
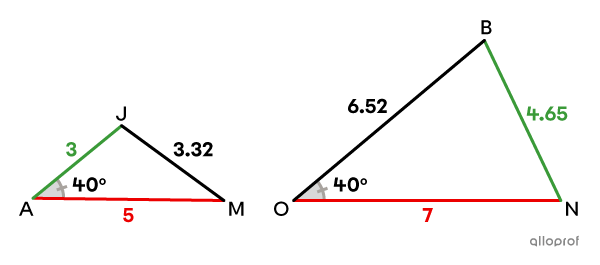
For example, in the above image, |\angle{JAM}| and |\angle{BON}| have the same measurement. However, angle |JAM| is situated between the small side and the big side of the triangle, which is not the case for angle |BON.| Therefore, the 2 triangles are not similar.
||\triangle JAM\color{#ec0000}\not\sim\triangle BON||
Triangles are similar if and only if they have 2 pairs of corresponding congruent angles.
Since the sum of the interior angles of a triangle is |180^\circ,| triangles that have 2 pairs of congruent corresponding angles necessarily have a 3rd pair of congruent angles. This minimum condition is therefore very practical since there is one less step to do and no side measurement is needed.
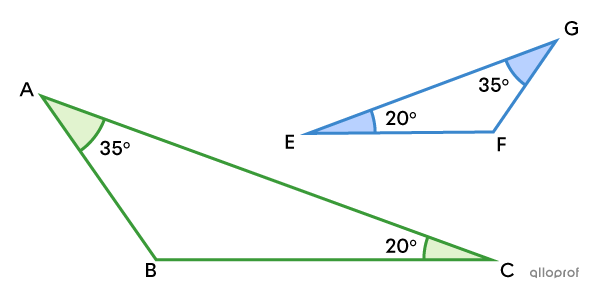
Prove that the following triangles |ABC| and |GEF| are similar.
| Statement | Justification | ||
|---|---|---|---|
|
1 |
Angles |A| and |G| are congruent.||\angle BAC\cong\angle FGE|| |
A |
By hypothesis. The information is given in the figure: |\text{m}\angle BAC=\text{m}\angle FGE=35^\circ.| |
|
2 |
Angles |C| and |E| are congruent.||\angle ACB\cong\angle GEF|| |
A |
By hypothesis. The information is given in the figure: |\text{m}\angle ACB=\text{m}\angle GEF=20^\circ.| |
|
3 |
Triangles |ABC| and |GFE| are similar. ||\triangle ABC\sim\triangle GFE|| |
They satisfy the minimum condition AA: triangles are similar if they have 2 pairs of corresponding congruent angles. |
|
After proving that triangles are similar, it is possible to find missing measures on either triangle, or to complete proofs. A table of statements and justifications is generally used for this type of problem.
Here are 3 examples where we use the minimum conditions to find a missing measurement.
Using the information provided in the problem, we must first prove that the triangles are similar before calculating missing measurements.
In the figure below, determine the measure of segment |\overline{AS}| knowing that it is parallel to segment |\overline{PT}.|

We cannot use the SSS condition, because the measures of several sides are missing. Moreover, we only know the measure of one side of triangle |BAS.| We cannot use the minimum condition SAS. Therefore, we must use AA.
| Statement | Justification | ||
|---|---|---|---|
|
1 |
Angles |ABS| and |TBP| are congruent. ||\angle ABS\cong\angle TBP|| |
A |
It is an angle that is common to both triangles. |
|
2 |
Angles |BAS| and |BTP| are congruent. ||\angle BAS\cong\angle BTP|| |
A |
Corresponding angles formed by parallel lines (|\overline{AS}| and |\overline{PT})| and cut by transversal |(\overline{AB})| are congruent. |
|
3 |
Triangles |ABS| and |TBP| are similar. ||\triangle ABS\sim\triangle TBP|| |
They satisfy the minimum condition AA: two triangles are similar if they have 2 pairs of corresponding congruent angles. |
|
|
4 |
Calculate the missing measurement using a proportion. |
The corresponding sides of similar triangles are proportional. |
|
Answer: Segment |\overline{AS}| measures |7.2\ \text{m}.|
Notes:
-
The theorem used to conclude the proof is a relationship between the angles that can be used in one of 2 ways:
-
If we know that the lines being cut by a transversal are parallel, then we can conclude that the pairs of alternate-interior, alternate-exterior and corresponding angles are congruent.
-
On the contrary, if we know that the lines being cut by a transversal form congruent pairs of alternate-interior, alternate-exterior or corresponding angles, then we can conclude that the lines are parallel.
-
-
The 1st interpretation was used in this example.
-
The problem in this example could have been solved using Thales's theorem, since the statement indicates that segments |\overline{AS}| and |\overline{PT}| are parallel.
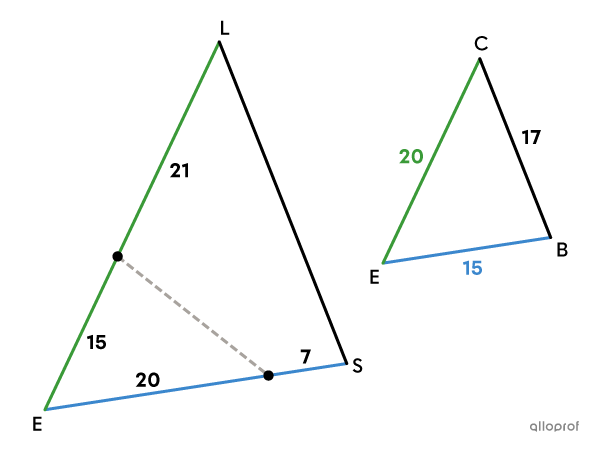
Find the measure of segment |\overline{SL}.|

We start by identifying the corresponding sides between triangles |BEC| and |SEL.| To help, we can position the triangles in the same way, like this:
-
|\color{#3b87cd}{\overline{BE}}| and |\color{#3b87cd}{\overline{SE}}| are corresponding sides because they are the smallest sides of their respective triangles.
-
|\color{#3a9a38}{\overline{CE}}| and |\color{#3a9a38}{\overline{LE}}| are corresponding sides because they are the biggest sides of their respective triangles.
-
|\overline{BC}| and |\overline{SL}| are therefore the last pair of corresponding sides.
Since we do not have the measure of all 6 sides (3 pairs of sides), we cannot use the minimum condition SSS to prove that the triangles are similar. So we use SAS.
| Statement | Justification | ||
|---|---|---|---|
|
1 |
There are 2 pairs of corresponding proportional sides. |
S |
|\color{#3b87cd}{\dfrac{\text{m}\overline{SE}}{\text{m}\overline{BE}}}=\dfrac{20+7}{15}=1.8| |
|
S |
|\color{#3a9a38}{\dfrac{\text{m}\overline{LE}}{\text{m}\overline{CE}}}=\dfrac{21+15}{20}=1.8| |
||
|
2 |
The corresponding angles |SEL| and |BEC| are congruent. |
A |
It is an angle common to both triangles. |
|
3 |
Triangles |BEC| and |SEL| are similar. ||\triangle BEC\sim\triangle SEL|| |
They satisfy the minimum condition SAS: triangles are similar if they have one pair of congruent angles located between 2 pairs of proportional corresponding sides. |
|
|
4 |
Calculate the missing measurement using a proportion. |
The corresponding sides of similar triangles are proportional. |
|
Answer: Segment |\overline{SL}| measures |30.6\ \text{units}.|
Find the measures of segments |\overline{AC}| and |\overline{AL}| in the following figure given that segments |\overline{CF}| and |\overline{BL}| are parallel.

Even if no angle measures are shown in the figure, we can still use the minimum condition AA.
| Statement | Justification | ||
|---|---|---|---|
|
1 |
Angles |CAF| and |LAB| are congruent.||\angle CAF\cong\angle LAB|| |
A |
Vertically opposite angles are congruent. |
|
2 |
Angles |AFC| and |ABL| are congruent.||\angle AFC\cong\angle ABL|| |
A |
Alternate-interior angles formed by parallel lines |(\overline{CF}| and |\overline{BL})|, and cut by a transversal |(\overline{BF})| are congruent. |
|
3 |
Triangles |FAC| and |BAL| are similar.||\triangle FAC\sim\triangle BAL|| |
They satisfy the minimum condition AA: triangles are similar if they have 2 pairs of congruent corresponding angles. |
|
|
4 |
Calculate the missing measurement using a proportion. |
The corresponding sides of similar triangles are proportional. |
|
Answer: Segment |\overline{AC}| measures |4.5\ \text{cm}| and segment |\overline{AL}| measures |10.5-4.5=6\ \text{cm}.|
Here is an example of a problem that uses minimum conditions to complete a proof.
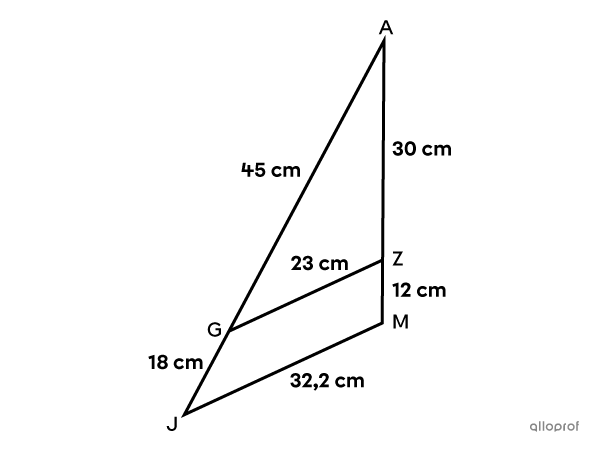
Prove that segments |\overline{GZ}| and |\overline{JM}| are parallel.
| Statement | Justification | ||
|---|---|---|---|
|
1 |
The corresponding sides are proportional. |
S |
|\dfrac{\text{m}\overline{AJ}}{\text{m}\overline{AG}}=\dfrac{45+18}{45}=1.4| |
|
S |
|\dfrac{\text{m}\overline{AM}}{\text{m}\overline{AZ}}=\dfrac{30+12}{30}=1.4| |
||
|
S |
|\dfrac{\text{m}\overline{JM}}{\text{m}\overline{GZ}}=\dfrac{32.2}{23}=1.4| |
||
|
2 |
Triangles |GAZ| and |JAM| are similar. ||\triangle GAZ\sim\triangle JAM|| |
They satisfy the minimum condition SSS: triangles are similar if their corresponding sides are proportional. |
|
|
3 |
Angles |AGZ| and |AJM| are congruent. ||\angle AGZ\cong\angle AJM|| |
In similar triangles, the corresponding angles are congruent. |
|
|
4 |
Segments |\overline{GZ}| and |\overline{JM}| are parallel. |
If 2 lines |(\overline{GZ}| and |\overline{JM})| are cut by a transversal |(\overline{AJ})| and form congruent corresponding angles |(\angle AGZ| and |\angle AJM),| the lines are parallel. |
|
Note:
-
The minimum condition SAS could be used for this problem.
-
The problem could have been solved using Thales’s Theorem.
-
Again, one of the relationships between the angles was used to complete the proof. This time, it was used to prove that the lines were parallel, knowing that the corresponding angles were congruent.
Pour valider ta compréhension à propos des démonstrations de façon interactive, consulte la MiniRécup suivante.
