La multiplication et la division sont des opérations qui se font avec des nombres positifs, mais aussi des nombres négatifs. Il faut donc s’assurer d’être à l’aise avec l’ensemble des nombres entiers. Il existe un lien étroit entre la multiplication et la division de nombres positifs et négatifs, puisque ce sont des opérations inverses l’une par rapport à l’autre. Les 2 opérations se font en suivant la règle des signes.
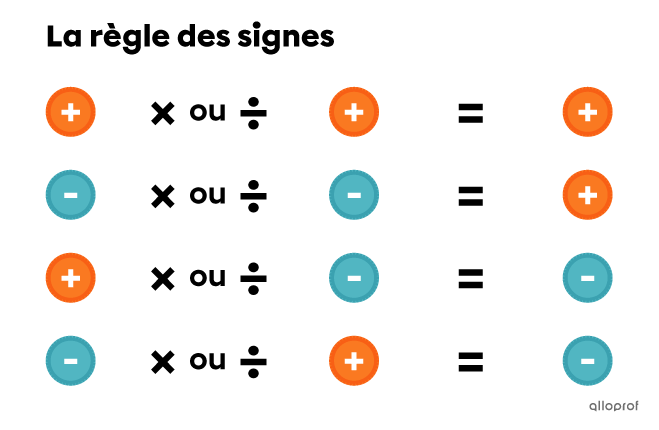
La règle des signes, aussi appelée loi des signes, permet de déterminer le signe du résultat d’une multiplication ou d’une division.
-
Si les 2 nombres multipliés ou divisés sont de même signe, le résultat est positif.
-
Si les 2 nombres multipliés ou divisés sont de signes contraires, le résultat est négatif.
Remarque : Cette loi des signes s’applique aussi dans le cas où les 2 signes sont collés dans une chaine d’opérations.
Voici le raisonnement qui explique les différents résultats obtenus à l’aide de la règle de signes. L’explication est donnée à l’aide de la multiplication, mais c’est le même principe pour la division.
On part du principe que |2| nombres positifs multipliés ensemble donnent un produit positif également.||3 \times 2 = 6||
Un nombre positif multiplié par un nombre négatif
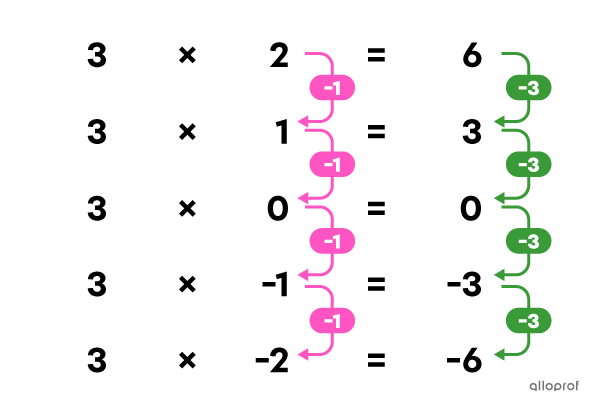
On cherche le résultat de l’opération |3 \times -2.| On commence à |3 \times 2,| et on diminue progressivement le 2e facteur. On constate que, chaque fois que le 2e facteur diminue de |\boldsymbol{\color{#ff55c3}1},| le produit diminue de |\boldsymbol{\color{#3a9a38}3}.| On détermine ainsi que lorsqu’on multiplie un nombre positif avec un nombre négatif, le produit est négatif.
Un nombre négatif multiplié par un nombre positif
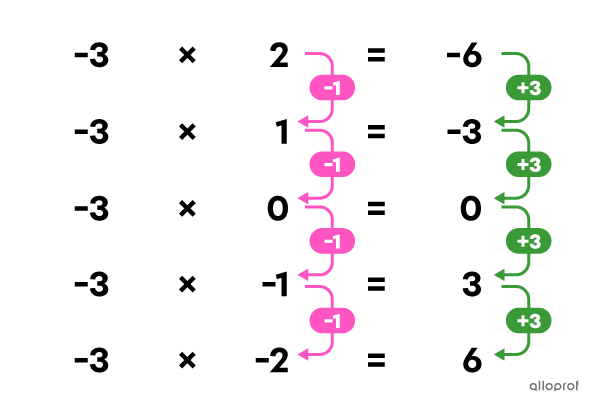
On cherche le résultat de l’opération |-3 \times 2.| On commence à |3 \times 2,| et on diminue progressivement le 1er facteur. On constate que, chaque fois que le 1er facteur diminue de |\boldsymbol{\color{#ff55c3}1},| le produit diminue de |\boldsymbol{\color{#3a9a38}2}.| On détermine ainsi que lorsqu’on multiplie un nombre négatif avec un nombre positif, le produit est négatif.

Un nombre négatif multiplié par un nombre négatif
On cherche le résultat de l’opération |-3 \times -2.| On commence à |-3\times 2.| On a déterminé que le résultat de ce calcul est négatif. On diminue progressivement le 2e facteur. On constate que, chaque fois que le 2e facteur diminue de |\boldsymbol{\color{#ff55c3}1},| le produit augmente de |\boldsymbol{\color{#3a9a38}3}.| On détermine ainsi que lorsqu’on multiplie un nombre négatif avec un nombre négatif, le produit est positif.
Pour faire une multiplication ou une division avec des nombres positifs et négatifs, il faut donc d’abord faire l’opération sans tenir compte des signes, puis déterminer le signe de la réponse à l’aide de la règle des signes. Cette technique s’applique autant pour multiplier des nombres décimaux et des fractions que pour diviser des nombres décimaux et des fractions.
Trouve le résultat de la multiplication |-15 \times 3.|
On commence par trouver le produit, sans tenir compte des signes.||15 \times 3 = 45||Selon la règle des signes, puisque les 2 facteurs sont de signes contraires, le résultat est négatif.
Réponse : Le résultat de la multiplication |-15 \times 3| est |-45.|
La règle des signes s’applique également avec les fractions, puisque les fractions représentent des divisions. Par convention, on met le signe « – » devant la fraction ou au numérateur, mais pas au dénominateur.||\begin{align}\dfrac{-15}{-4}\ &\Rightarrow\ \dfrac{15}{4}\\[3pt] \dfrac{2}{-3}\ &\Rightarrow\ -\dfrac{2}{3}\end{align}||
S’il y a une chaine d’opérations avec plusieurs multiplications ou divisions, et qu’on veut déterminer le signe du résultat final, il faut compter le nombre de « – ». S’il y en a un nombre pair, le résultat est positif. S’il y en a un nombre impair, le résultat est négatif.
Trouve le résultat de la chaine d’opérations |-452 \div -16 \times 12 \times 2 \div -15.|
On effectue d’abord les calculs, sans tenir compte des signes.||\begin{align}&452 \div 16 \times 12 \times 2 \div 15\\=\ &28{,}25 \times 12 \times 2 \div 15\\=\ &339 \times 2 \div 15\\=\ &678 \div 15\\=\ &45{,}2 \end{align}||Comme il y a 3 nombres négatifs dans la chaine d’opérations |(-452,| |-16| et |-15),| le résultat est négatif.
Réponse : Le résultat de la chaine d’opérations |-452 \div -16 \times 12 \times 2 \div -15| est |-45{,}2.|