The set of natural numbers, represented by the symbol |\mathbb{N},| includes all the numbers used for counting.||\mathbb{N} = \{0,1,2,3,4,5,\ldots\}||This set of numbers is sometimes referred to as whole numbers.
Natural numbers are all the positive integers, including |0.| Integers are numbers that have no decimal places or whose decimal part is zero.
One definition of natural numbers does not include the number |0.| To avoid confusion, we use the notation |\mathbb{N}^{*}| to denote the set of natural numbers excluding |0.| ||\mathbb{N}^{*} = \{1,2,3,4,5,\ldots\}||
On a number line, natural numbers can be represented by points in the positions of whole numbers.
The orange dots on the number line below represent the first elements of the natural numbers.

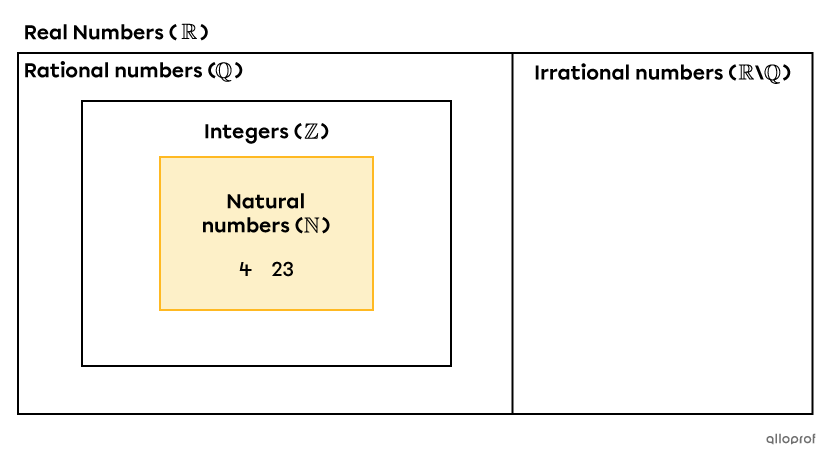
Here's a diagram that illustrates the position of the natural numbers |(\mathbb N)| within the set of real numbers |(\mathbb R).|
-
The number |0,| the number |28| and the number |492\ 683| are 3 natural numbers.
-
The number represented by |\dfrac{6}{2}| is a natural number since it corresponds to the number |3.| However, the number |\dfrac{6}{5}| is not a natural number since it corresponds to the number |1.2.|
-
The number |5| is a natural number, but the number |-5| is not, since it's a negative number.
-
Using the appropriate notation, we get |28 \in \mathbb{N}| and |\dfrac{6}{5} \notin \mathbb{N}.|