Numbers are classified into different sets according to their characteristics. The diagram below illustrates the relationships between them.
Similar to how words are made up of letters of the alphabet, numbers are formed by the combination of digits. It is important to understand the rules for writing numbers when working with them. Numbers allow us to mathematically express the size of things around us.
The number |6| represents the number of stars contained in the set.

The number |-2| is represented by the position of point |\color{#fa7921}{A}| on the number line.

The number |72.95| represents the cost in dollars of a pair of shoes.

Numbers can be arranged in ascending or descending order. They can also be classified into sets according to their characteristics.
Numbers are classified into different sets according to their characteristics. The diagram below illustrates the relationships between them.
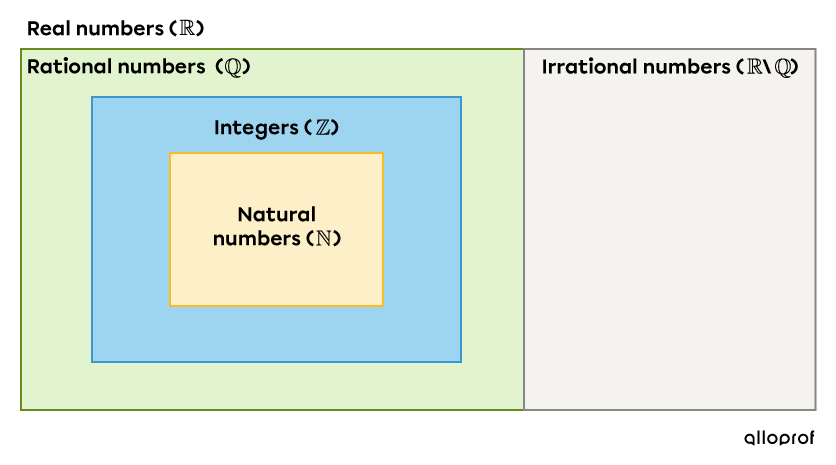
As illustrated in this diagram, the set of natural numbers is included in the set of integers. The set of integers is in turn included in the set of rational numbers. The set of real numbers is composed of the union of the sets of rational numbers and irrational numbers. The following table gives an overview of the different sets.
|
Number set |
Description |
Examples |
|---|---|---|
|
Natural numbers |
Numbers used for counting |
|3,\ ||5,\ ||134,\ ||2099| |
|
Integers |
Natural numbers and their opposites |
|-133,\ ||-9,\ ||0,\ ||9,\ ||915| |
|
Rational numbers |
Numbers that can be expressed as the ratio of 2 integers |
|-5.\overline{3},\ ||-\dfrac{1}{3},\ ||\dfrac{3}{4},\ ||3,\ ||6.4| |
|
Irrational numbers |
Numbers that cannot be expressed as the ratio of 2 integers |
|\sqrt{2},\ ||\sqrt[3]{11},\ ||e,\ ||\pi| |
|
Real numbers |
Numbers that belong to either the set of rational numbers or the set of irrational numbers |
|-16,\ ||\dfrac{5}{8},\ ||\sqrt{5},\ ||7,\ ||23.\overline{6}| |
We sometimes also consider the set of decimal numbers |(\mathbb{D}).| This consists of all the rational numbers whose decimal expansion is finite, rather than periodic. This set forms a subset of the rational numbers, which includes the set of integers.
Certain symbols are commonly used for number set notation. The following table summarizes the list of these symbols.
|
Symbol |
Definition |
Example |
|---|---|---|
|
|\{\ ,\,\}| |
Listing the elements of a set in expanded form |
|\{0,1,2,3,4,...\}| |
|
|\in| |
"... belongs to..." or "... is an element of..." |
|3\in \mathbb{N}| |
|
|\notin| |
"... does not belong to..." or "... is not an element of..." |
|\mathbb{Z}\subset\mathbb{Q}| |
|
|\subset| |
"... is included in..." or "... is a subset of..." |
|\mathbb{Z}\subset\mathbb{Q}| |
|
|\large\cup| |
Union of 2 sets |
|\mathbb{R}=\mathbb{Q} \cup \mathbb{Q’}| |
|
|\tiny\boxed{\phantom{\normalsize{t}}}^{\large*}| |
Excluding the number zero |
|\mathbb{N}^*| represents the set of natural numbers excluding |0.| |
|
|\tiny\boxed{\phantom{\normalsize{t}}}_{\large+}| |
Only the positive elements of the set |
|\mathbb{Z}_+| represents the set of positive integers. |
|
|\tiny\boxed{\phantom{\normalsize{t}}}_{\large-}| |
Only the negative elements of the set |
|\mathbb{Q}_-| represents the set of only negative rational numbers. |