When solving a situational problem using the exponential function, it is usually expressed in the functional form |y=a(c)^{bx}.|
||f(x)=a(c)^{bx}||
where
|a:| Initial Value
|c:| Multiplier
|b:| The number of times to apply the multiplier over a given period (determined by |x|)
The following are the steps to solve a problem using the exponential function:
-
Identify the variables.
-
Find the rule of the function:
-
Determine the value of |a.|
-
Determine the value of |c.|
-
Determine the value of |b.|
-
-
Answer the question.
Parameter |a| is the initial value.
Parameter |c| is the positive multiplier determined from the number |1| (which corresponds to |100\%|).
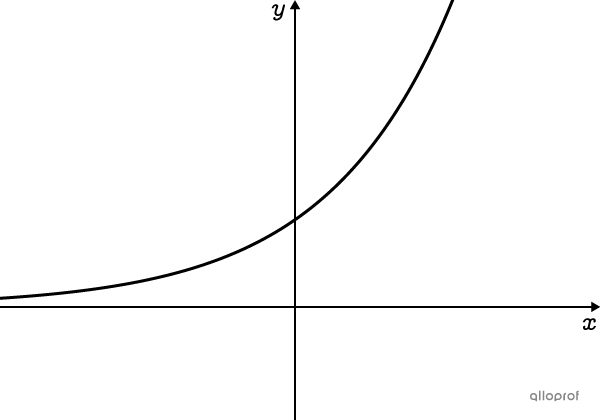
When |\boldsymbol{c>1,}| the function increases (if |\boldsymbol{a>0}|), because its multiplier is greater than |\boldsymbol{1.}|
-
The value triples.||c=3\times1=3||
-
The investment increases at a rate of |10\ \%| per year. ||c=1+0.1=1.1||
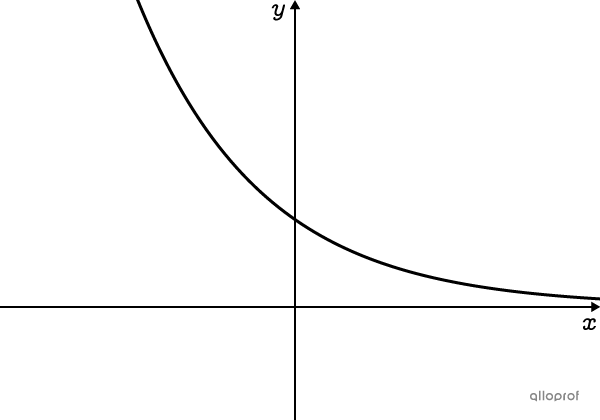
When |\boldsymbol{0<c<1,}| the function is decreasing (if |\boldsymbol{a>0}|), because its multiplier is less than |\boldsymbol{1}.|
-
The value decreases by |15\ \%.|||c=1-0.15=0.85||
-
An amount is losing a fourth of its value every month.||c=1-\dfrac{1}{4}=\dfrac{3}{4}||
Parameter |b| is determined by the number of times the event occurs (how many times the multiplier is used) for the given period determined according to |x.|
The event occurs several times over the given period.
The event occurs every 3 months and the |x| variable is in years. There are 4 events per year.||b=4||

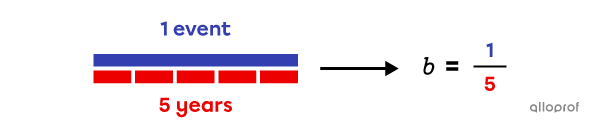
The event takes more than one period to occur.
The event occurs every 5 years, but the variable |x| is in years. There is 1 event every 5 years.||b=\dfrac{1}{5}||
To solve a problem involving the exponential function, we must solve the exponential equation or inequality.
Ash bought a beautiful new electric car worth |$45\ 000|. Auto insurance experts estimate that an electric car loses an average of |20\ \%| of its value each year. Knowing this, what will Ash's car be worth after |8| years?
-
Identify the variables
|x:| Time elapsed (in years) since Ash bought the car.
|f(x):| Value ($) of the vehicle. -
Find the rule
-
Determine the value of |\boldsymbol{a}|
It is the initial price of the car.||a=45\ 000|| -
Determine the value |\boldsymbol{c}|
If the car loses |20\ \%\ (0.2)| of its value each year, we can calculate c: |1-0.2=0.8.|||c=0.8|| -
Determine the value of |\boldsymbol{b}|
The event occurs once a year and the variable |x| is the number of years, so:||b=\dfrac{\color{#333fb1}1}{\color{#EC0000}1}=1||
The rule for the exponential function is |f(x)=45\ 000(0.8)^x|
-
-
Answer the question
We want to find the value of Ash's car after |8| years. Replacing |x| by |8,| we find the value of |f(8).|||\begin{align}f(x)&=45\ 000(0.8)^{x}\\f(8)&=45\ 000(0.8)^8\\
&\approx$7\ 549.75\ \end{align}||Therefore, after |8| years, Ash's car will be worth approximately |$7\ 549.75.|
It is possible to change the units of the variable |x| in a problem. However, we must make sure to make the appropriate changes to the rule as well.
In the previous example, we could have worked in months instead of years. Since the event still occurs once a year (or once every 12 months), so in this case |b=\dfrac{1}{12}.| To answer the question about the car’s value in |8| years, we would have had to replace |x| by |96| months. Then the answer would have been the same.
It is also possible to find the rule in the previous example by using a table of values. We know the purchase price is |$45\ 000| and that each year it retains only |80\ \%| of its value from the previous year.
|
|\boldsymbol{x:}| Time elapsed (in years) since Ash bought the car |
|\boldsymbol{f(x):}| Value of the vehicle ($) |
|
|---|---|---|
|
|0| |
|45\ 000| |
|45\ 000| |
|
|1| |
|\color{#3a9a38}{45\ 000}\times 0.8| |
|45\ 000\times(0.8)^1| |
|
|2| |
|\color{#3a9a38}{45\ 000\times 0.8}\times 0.8| |
|45\ 000\times(0.8)^2| |
|
|3| |
|\color{#3a9a38}{45\ 000\times 0.8\times 0.8}\times 0.8| |
|45\ 000\times(0.8)^3| |
|
... |
... |
... |
|
|x| |
|\color{#3a9a38}{45\ 000\ \times\ }\underbrace{\color{#3a9a38}{0.8\times0.8\times\ldots}\times0.8}_{x\text{ times}}| |
|45\ 000\times(0.8)^x| |
From the table, we can determine that the rule of the function is |f(x)=45\ 000(0.8)^x|
At the start of an experiment, a researcher has |50\ \text{g}| of a radioactive element. The element decays at a rate where its mass decreases by one half, |3| times every hour. What is the exponential function rule that represents the situation?
-
Identify the variables
|x:| Time elapsed (in hours) since the start of the experiment
|f(x):| The mass (in grams) of the radioactive element -
Find the rule of the function
-
Determine the value of |\boldsymbol{a}|
Since the researcher has |50\ \text{g}| of the element at the beginning of the experiment, the initial value is |50.|||a=50|| -
Determine the value of |\boldsymbol{c}|
Since the mass of the radioactive element decreases by one half over each period, the multiplier is |\dfrac{1}{2}.|||c=\dfrac{1}{2}|| -
Determine the value of |\boldsymbol{b}|
Since |x| is the number of hours, we must find how many times the event occurs each hour. We know the radioactive element decreases |\color{#333fb1}3| times per hour.||b=\dfrac{\color{#333fb1}3}{\color{#EC0000}1}=3||
-
-
Answer the question
Therefore, the rule for the exponential function representing the situation is |f(x)=50\left(\dfrac{1}{2}\right)^{3x}|
At |8\ \text{am}| this morning, a cup of yogurt on a countertop contained |10\ 000| bacteria. At room temperature, the bacteria count quadruples every |2| hours. If yogurt is considered inedible when it contains |640\ 000| or more of bacteria, after how many hours will the yogurt be inedible?
-
Identify the variables
|x:| Time elapsed (in hours) since |8\ \text{am}|
|f(x):| Bacteria count in the cup of yogurt -
Find the rule
-
Determine the value of |\boldsymbol{a}|
At |8\ \text{am}| (when |x=0|), the bacteria count is |10\ 000.|||a=10\ 000|| -
Determine the value of |\boldsymbol{c}|
Since the bacteria count quadruples in each period, the multiplier is||c=4|| -
Determine the value of |\boldsymbol{b}|
Since |x| is the number of hours elapsed, we determine how many times the event occurs per hour. The bacteria multiply |\color{#333fb1}1| times every |\color{#EC0000}2| hours.||b=\dfrac{\color{#333fb1}1}{\color{#EC0000}2}||
Therefore, the exponential function rule is |f(x)=10\ 000 (4)^{\!^{\large\frac{x}{2}}}|
-
-
Answer the question
We want to know after how many hours the bacteria count will exceed |640\ 000|, so we must solve the following inequality:
||10\ 000 (4)^{\!^{\large\frac{x}{2}}}>640\ 000||
Replace the symbol |>| with |=| and solve.
||\begin{align}10\ 000 (4)^{\!^{\large\frac{x}{2}}}&=640\ 000\\(4)^{\!^{\large\frac{x}{2}}}&=64\end{align}||
Switch to logarithm form and isolate |x.|
||\begin{align}\dfrac{x}{2}&=\log_4 64\\\dfrac{x}{2}&=3\\x&=6\end{align}||
Since the bacteria count in the yogurt will increase, we should throw it in the trash after |6| hours.
There is a special case where we can use exponential functions to analyze investments or loans with interest in financial mathematics. The parameters |a| and |b| have the same roles, however, if the interest is compounded annually, or otherwise, then parameter |c| changes.
||\begin{align}f(x)&=a(c)^{bx}\\
f(x)&=a\left(1\pm\dfrac{i}{b}\right)^{bx}\end{align}||where
|a:| initial value
|c:| multiplier (tied to the interest rate)
|b:| number of times per period the interest is calculated
|i:| interest rate (in decimal form)
The symbol |+| is used for a increase in value and the symbol |-| for a decrease in value.
After getting a student job and working all summer, Alex has managed to save |\$4\ 000.| He invests his savings at an annual interest rate of |3\ \%| compounded monthly. After how long will his investment grow to a value of |\$6\ 000|?
-
Identify the variables
|x:| Time elapsed (in years) since Alex invested his savings
|f(x):| Value of his investment |($)| -
Find the rule
-
Determine the value of |\boldsymbol{a}|
The initial amount is |\$4\ 000.|||a=4\ 000|| -
Determine the value of |\boldsymbol{c}|
Since the interest rate is |3\ \%\ (0.03)| compounded monthly (|12| months in a year), we obtain:||\begin{align}c&=1+\dfrac{0.03}{12}\\&=1.0025\end{align}|| -
Determine the value of |\boldsymbol{b}|
The variable |x| is years, but the interest is compounded each month. Therefore, the interest calculated is |\color{#333fb1}{12}| times in |\color{#EC0000}1| year.||b=\dfrac{\color{#333fb1}{12}}{\color{#EC0000}1}=12||
Therefore, the exponential function rule is |f(x)=4\ 000(1.0025)^{12x}.|
-
-
Answer the question
We want to know how long it will take for Alex’s investment to reach |$\ 6\ 000.| So, we replace |f(x)| by |6\ 000| and isolate |x.|||\begin{align}6\ 000&=4\ 000(1.0025)^{12x}\\1.5&=(1.0025)^{12x}\end{align}||We switch to a logarithm form and find the value of |x| by applying the change of base law for logarithms.||\begin{align}12x&=\log_{1.0025}1.5\\12x&=\dfrac{\log1.5}{\log{1.0025}}\\12x&\approx162.39\\x&\approx13.53\end{align}||Therefore, Alex's investment will be worth |\$6\ 000| after approximately |13.5| years.
Pour valider ta compréhension à propos de la résolution de problèmes impliquant la fonction exponentielle de façon interactive, consulte la MiniRécup suivante.
