Radioactivity is the phenomenon whereby the nucleus of an unstable atom decays by emitting high-energy particles and/or radiation.
When an atom’s unstable nucleus decays, a nuclear transformation occurs and stabilizes the nucleus. This process is accompanied by one or more types of radiation: alpha radiation |(\alpha),| beta radiation |(\beta)| and gamma radiation |(\gamma).|
Radioactivity has various applications and impacts, such as dating ancient objects, generating energy, developing medical treatments and more. Evaluating an atom’s half-life can reveal its ability to decay and how this decay can be used.
Radioactivity is a natural phenomenon discovered by physicist Henri Becquerel, in 1896. There are several ways to measure the radioactivity of a substance. For example, the becquerel per gram method |(\text{Bq/g})|, named after the physicist, calculates the number of atoms that decay per second for each gram of decaying matter. This is called specific activity.
The table below shows a comparison of different sources of radioactivity.
| Source | Approximate specific activity |(\text{Bq/g})| |
|---|---|
| Human body | |0.120| |
| Banana | |0.110| |
| Sea water | |0.013| |
| Uranium ore | |10\ 000| |
| Plutonium-239 | |2\ 300\ 000\ 000| |
Data source: Institute for Radiological Protection and Nuclear Safety, 2021.
While alpha |(\alpha)| and beta |(\beta)| radiation are forms of particle radiation, gamma radiation |(\gamma)| is electromagnetic. These properties influence the ability of the radiation to penetrate matter. For instance, gamma |(\gamma)| radiation has greater penetration capacity than alpha |(\alpha)| and beta |(\beta)| particles. Smaller and lighter beta particles |(\beta)| have greater penetration capacity than alpha particles |(\alpha).|
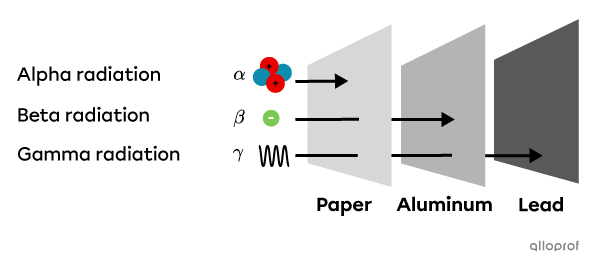
The following diagram shows the penetration capacity of different types of radiation.
-
Alpha radiation |(\alpha)| cannot penetrate a sheet of paper, nor can it penetrate the skin.
-
Beta radiation |(\beta)| can penetrate a sheet of paper but not a sheet of aluminum. It can also penetrate the surface of the body but poses no significant health risk.
-
Gamma |(\gamma)| radiation can penetrate paper and aluminum but can be absorbed by lead. It can also pass through the body and poses a significant health risk.
These three types of radiation carry a lot of energy. When penetrating matter, they can create ions, which is why they are also known as ionizing radiation. This can be beneficial or dangerous to human health, depending on how the exposure occurs.
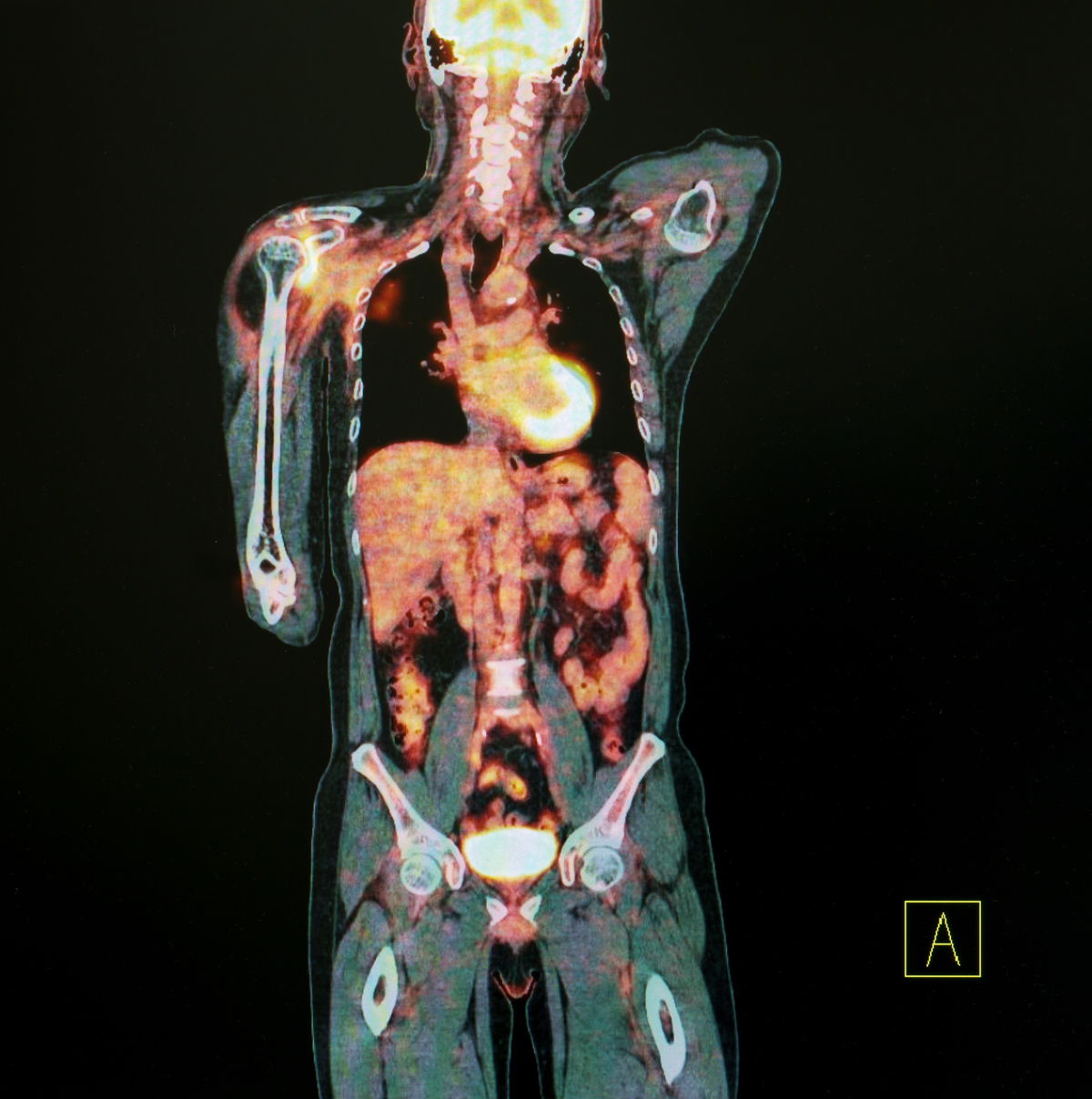
Positron Emission Tomography (PET) uses gamma rays to generate images that doctors use to make diagnoses.
Monet_3k, Shutterstock.com
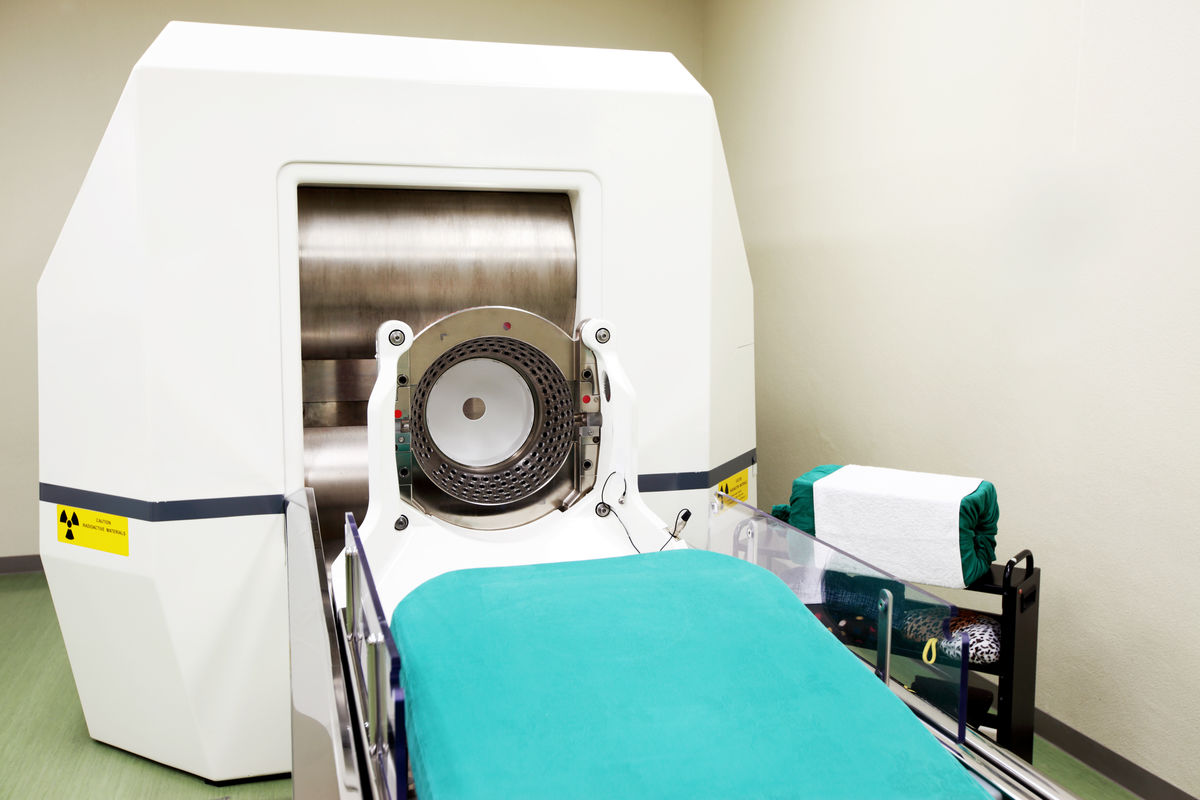
Gamma radiation |(\gamma)| can be used in radiotherapy treatment since it is able to destroy cancerous tissue. For example, Gamma Knife radiosurgery is a treatment that can very precisely destroy brain tumours using precise gamma rays.
Alexander Gatsenko, Shutterstock.com
The Chernobyl nuclear disaster in Ukraine (1986) and the Fukushima nuclear disaster in Japan (2011) were the worst in history. Each one released a huge amount of radioactive radiation, which harmed many people by causing genetic mutations resulting in cancers and birth defects. The soil, air and rivers were all highly contaminated.

Presslab, Shutterstock.com
The half-life |(t_{1/2})| of an isotope is the time required for half of the atoms in a sample to decay.
It also indicates the stability of an isotope.
In a highly unstable isotope, it takes very little time for half of the atoms in a sample to decay, so the half-life is short. For example, bohrium-271 |(^{271}\text{Bh})| is very unstable, with a half-life of just |1.2| seconds.
In a highly stable isotope, it takes much more time for half of the atoms in a sample to decay, so the half-life is long. For example, iodine-129 |(^{129}\text{I})| has a half-life of |15.7| million years.
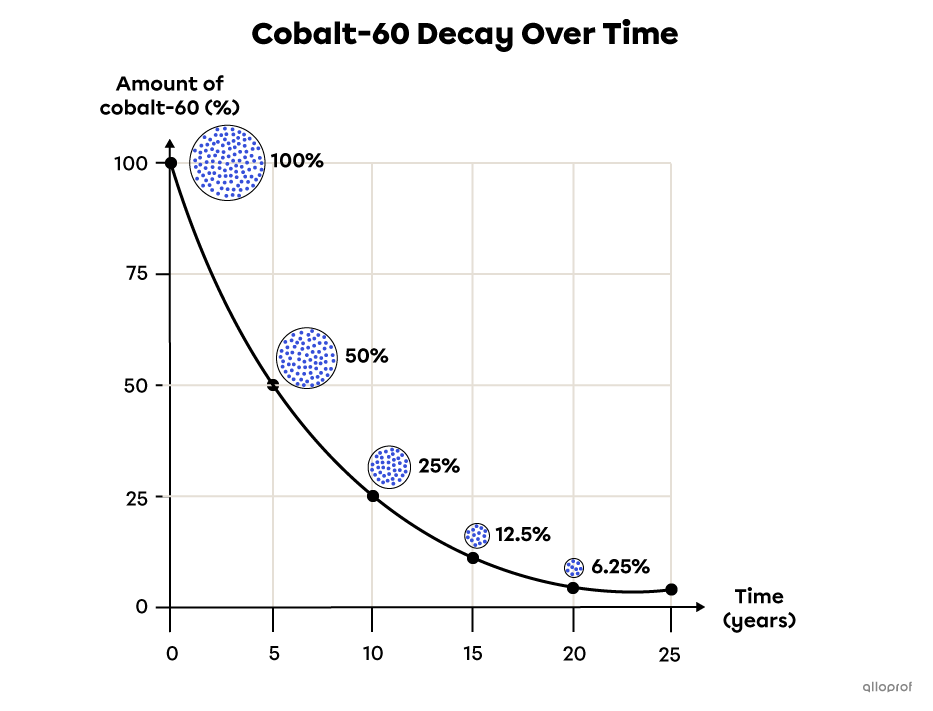
This graph shows the amount of remaining cobalt-60 over time. After approximately 5 years, 50% of the cobalt sample is decayed. Therefore, the half-life of cobalt-60 is about 5 years, with 50% of the initial sample remaining.
It would take 5 years for half of the remaining cobalt to decay (25%), then another 5 years for half that remaining 25% to decay (12.5%), and so on.
Uranium mining generates several types of radioactive waste such as radium-226 |(^{226}\text{Ra}),| thorium-230 |(^{230}\text{Th}),| various barium isotopes |(\text{Ba})| and many others. The half-lives of these isotopes can vary from a few seconds to several thousand years, which makes it challenging to safely store this waste.

John Carnemolla, Shutterstock.com
The half-life concept can also be used to date archaeological specimens using carbon, uranium and even lead.
Most of the carbon found on our planet is carbon-12 |(^{12}_{6}\text{C}),| but there are also small amounts of other isotopes such as carbon-13 |(^{13}_{6}\text{C})| and carbon-14 |(^{14}_{6}\text{C}),| which is used for carbon-14 dating of specimens containing carbon.
In living organisms, the concentration of carbon-14 is stable. When an organism dies, its carbon-14 concentration diminishes over time. Since the half-life of carbon-14 is about 5 730 years, it is possible to use this information to determine the age of archaeological specimens.
For example, if the carbon-14 concentration of an animal’s remains is twice as low as it would normally be, this means that a half-life has gone by since it died. The animal would have lived about 5 730 years ago.

Dtopal, Shutterstock.com
Alpha particles |(\alpha)| can be represented in various ways.
| |^4_2\text{He}^{2+}| | |^4_2\text{He}| | |\alpha| | |^4_2\alpha| |
Alpha particles |(\alpha)| are generally emitted by atoms with a heavy nucleus and will decay to create an atom with a lighter nucleus. Using the A/Z notation, sometimes called the Berzelius’ notation, this type of transformation can be illustrated as follows.
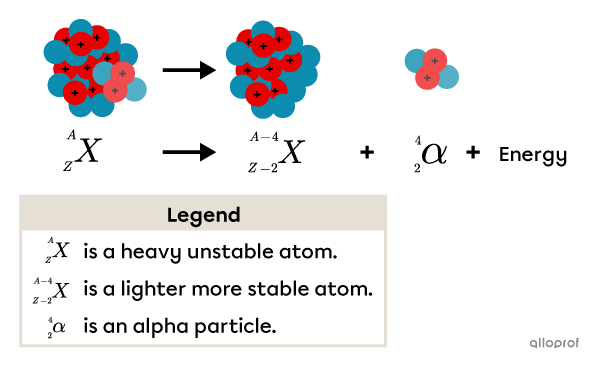
Alpha radiation |(\alpha)| emission creates the following changes:
-
The decaying atom loses 2 neutrons and 2 protons.
-
Its atomic number |(Z)| decreases by 2.
-
Its mass number |(A)| decreases by 4.
-
The atom produced by the nuclear reaction is lighter and more stable because there is a more balanced ratio between the number of protons and neutrons.
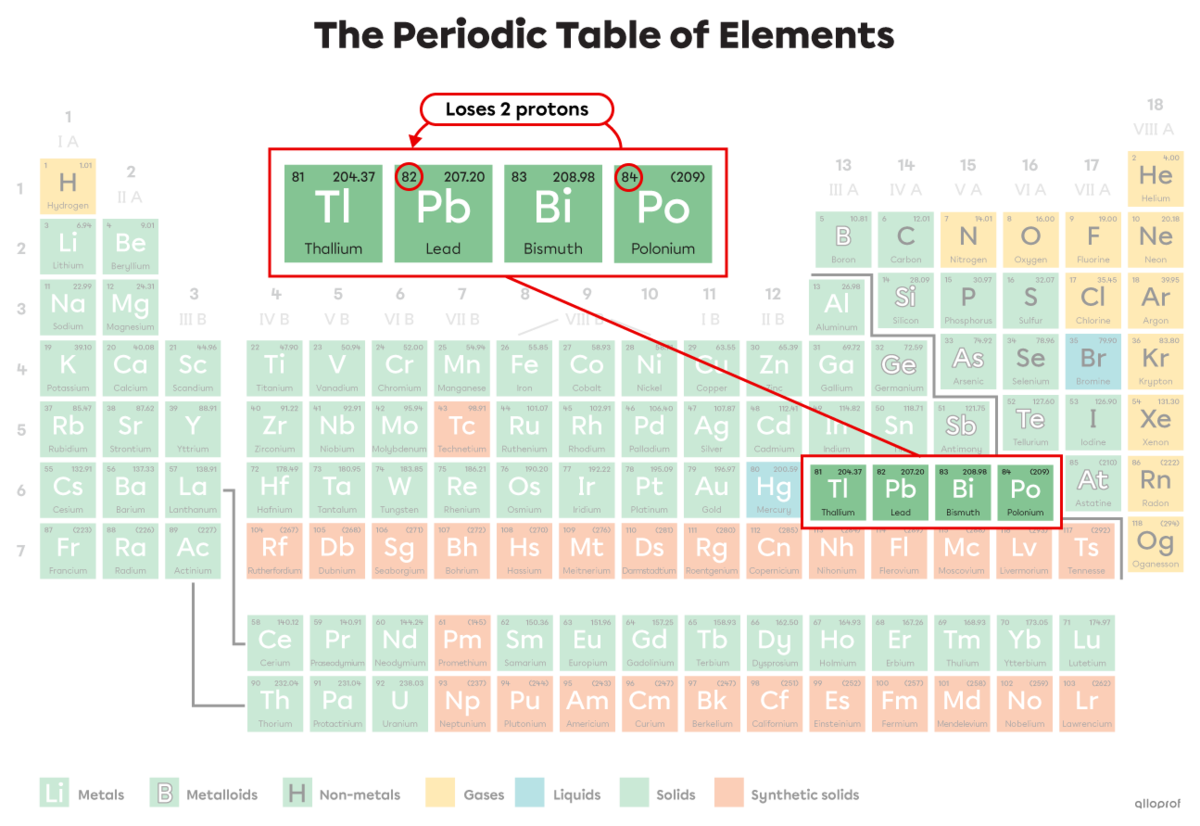
In 1903, Marie Curie received the Nobel Prize in Physics for her radioactivity research. Among other things, she studied the radioactivity of polonium that decays according to the following nuclear fission reaction.
||^{218}_{84}\text{Po}\ \rightarrow\ ^{214}_{82}\text{Pb} \ +\ ^4_2\alpha||
During this nuclear reaction, a few things can be observed.
-
An alpha particle is emitted |(^4_2\alpha).|
-
The mass number |(A)| of polonium |(\text{Po})| decreases from 218 to 214 because polonium loses 4 nucleons (2 protons and 2 neutrons that become alpha particles |(\alpha).|
-
The atomic number |(Z)| of polonium |(\text{Po})| decreases from 84 to 82 because it loses 2 protons. The polonium atom |(\text{Po})| becomes a lead atom |(\text{Pb})|. The lead-214 atom is lighter and more stable than the polonium-218 atom.
Beta radiation |(\beta),| also called a beta particle, is a very light and high energy particle.
A beta particle |(\beta)| with a positive charge is a positron and a beta particle |(\beta)| with a negative charge is an electron. This concept sheet will focus solely on negative beta particles.
Negative |\beta| particles can be represented in various ways.
| |\text{e}^-| | |\beta| | |\beta^-| | |^0_{-1}\beta| |
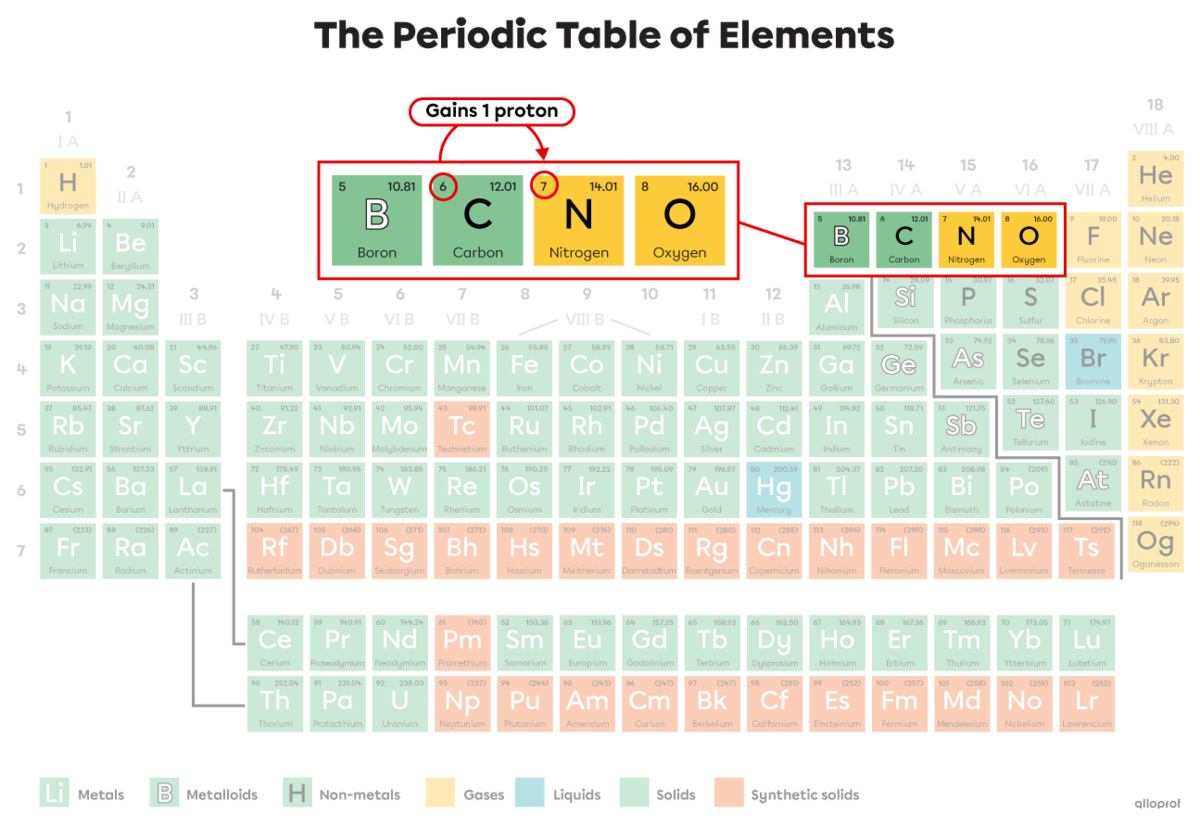
Beta particles |(\beta)| are generally emitted when a light atom contains too many neutrons. The atom’s nucleus decays, transforming a neutron into a proton and emitting a beta particle |(\beta).|
Based on an early 20th century model, this transformation can be represented using the A/Z notation.

Beta radiation |(\beta)| emission creates the following changes:
-
The decaying atom loses 1 neutron and gains 1 proton.
-
Its atomic number |(Z)| increases by 1.
-
Its mass number |(A)| remains the same.
-
The atom produced by this nuclear reaction has essentially the same mass as before, but is more stable due to a more balanced ratio between the number of protons and neutrons.
Carbon-14 is a radioactive isotope of carbon that decays by beta radiation |(\beta)| as shown in the following equation.
||^{14}_{6}\text{C}\ \rightarrow\ ^{14}_7\text{N}\ +\ ^0_{-1}\beta||
During this nuclear reaction, a few things can be observed.
-
A beta particle is emitted |(^0_{-1}\beta).|
-
The mass number |(A)| of the atom remains the same (14). In other words, the total number of neutrons and protons remains the same.
-
The atomic number |(Z)| changes from 6 to 7. Initially, carbon-14 |(^{14}_{6}\text{C})| has 6 protons and 8 neutrons. It transforms into nitrogen-14 |(^{14}_{7}\text{N}),| which has 7 protons and 7 neutrons. During the reaction, 1 neutron is transformed into 1 proton.
-
The carbon atom |(\text{C})| becomes a nitrogen atom |(\text{N}).| This nitrogen-14 atom has almost the same mass as the carbon-14 atom but with 1 more proton and 1 less neutron.
The previous example explains that an atom decaying by beta radiation |(\beta)| generates another atom and a beta particle |(\beta).| In the 1920s, many physicists realized that this decay did not respect the law of conservation of mass: the atom’s mass prior to decay |(m_\text{initial})| is not exactly the same as the mass of the new atom and a beta particle |(m_\text{final}).|
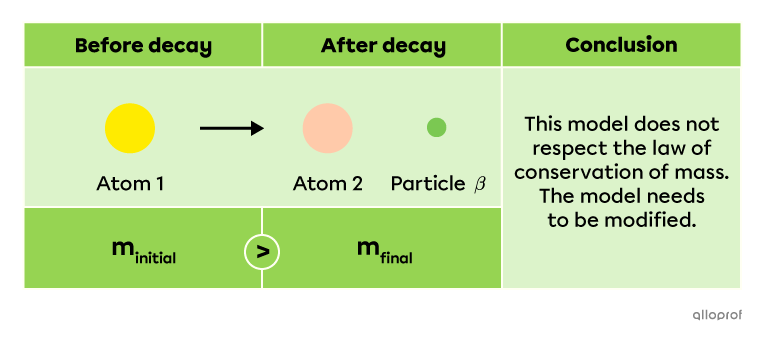
This strange discovery led physicist Wolfgang Pauli to conclude that another particle must be emitted during this reaction. This particle is a neutrino |(\nu),| a very light and neutral elementary subatomic particle. The following model is a more accurate way to represent decay by beta radiation |(\beta)|.

The A/Z notation can be used to describe this nuclear reaction.
|^{A}_Z\text{X}\ \rightarrow\ ^{A}_{Z+1}\text{X}\ +\ ^0_{-1}\beta\ +\ ^0_0\nu\ +\ \text{Energy}|
Gamma radiation |(\gamma),| commonly referred to as gamma rays, is high energy electromagnetic radiation with no mass.
Gamma radiation |(\gamma)| can be represented in various ways.
| |\gamma| | |^0_0\gamma| |
Gamma radiation |(\gamma)| often occurs during decay by alpha |(\alpha)| or beta |(\beta)| radiation reactions. It can also be created when a high energy atom loses its energy. The atom is said to change from an excited state to a ground state.
The A/Z notation can be used to explain this emission of energy.

A high energy cobalt atom |^{60}_{27}\text{Co}^*| emits gamma rays |\gamma| as shown in the following equation:
|^{60}_{27}\text{Co}^*\ \rightarrow\ ^{60}_{27}\text{Co}\ +\ ^0_0\gamma|
During this nuclear reaction, a few things can be observed.
-
A large amount of energy is emitted as gamma radiation |(\gamma).|
-
The mass number |(A = 60)| and atomic number |(Z = 27)| of cobalt remains the same.
-
There is no change in the number of neutrons, protons or electrons of cobalt-60. It emits only energy.
Institut de radioprotection et de sûreté nucléaire. (2021). La radioécologie marine.
https://www.irsn.fr/FR/connaissances/Environnement/radioactivite-environnement/radioecologie/Pages/5-radioecologie-marine.aspx#.X41akkE6-70
Institut de radioprotection et de sûreté nucléaire. (2021). Les sources de radioactivité naturelle.
https://www.irsn.fr/FR/connaissances/Environnement/radioactivite-environnement/sources-radioactivite/Pages/1-sources-radioactivite-naturelle.aspx