Lorsqu'on traduit une situation avec une fonction exponentielle, on utilise généralement la forme |y=a(c)^{bx}.|
||f(x)=a(c)^{bx}||
où
|a :| Valeur initiale
|c :| Facteur multiplicatif
|b :| Nombre de fois que le facteur multiplicatif est appliqué dans une période donnée (déterminée à partir de |x|)
Voici les étapes principales à suivre pour résoudre un problème à l’aide de la fonction exponentielle.
-
Identifier les variables.
-
Déterminer la règle de la fonction.
-
Déterminer la valeur de |a.|
-
Déterminer la valeur de |c.|
-
Déterminer la valeur de |b.|
-
-
Répondre à la question.
Le paramètre |a| est la valeur initiale de la situation.
Le paramètre |c| est le facteur multiplicatif positif qu’on détermine à partir du nombre |1| (qui correspond à |100\ \%|).
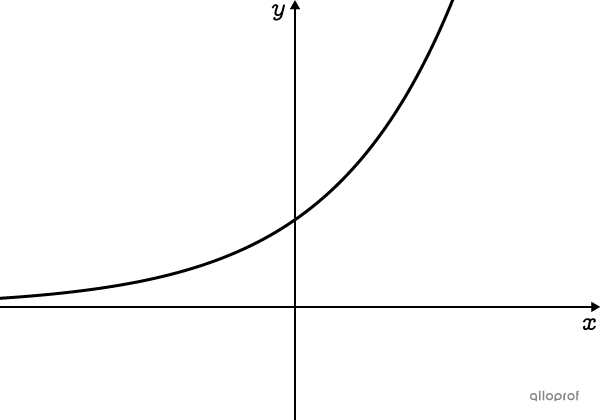
Avec |\boldsymbol{c>1,}| la valeur augmente (si |\boldsymbol{a>0}|), car on la multiplie par un nombre supérieur à |\boldsymbol{1.}|
-
La valeur triple.||c=3\times1=3||
-
Les intérêts augmentent le montant à un taux de |10\ \%.|||c=1+0{,}1=1{,}1||
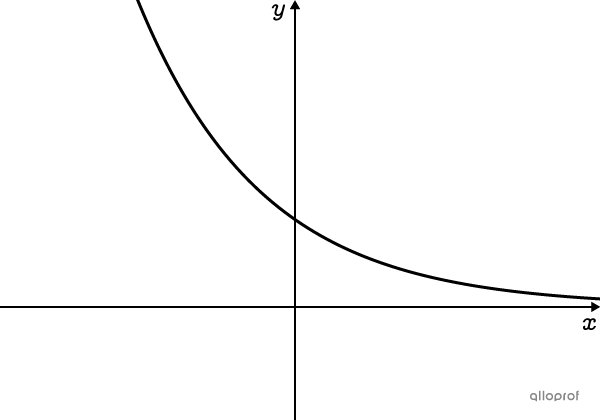
Avec |\boldsymbol{0<c<1,}| la valeur diminue (si |\boldsymbol{a>0}|), car on la multiplie par un nombre inférieur à |\boldsymbol{1.}|
-
La valeur diminue de |15\ \%.|||c=1-0{,}15=0{,}85||
-
Le montant perd le quart de sa valeur.||c=1-\dfrac{1}{4}=\dfrac{3}{4}||
Le paramètre |b| se trouve à partir du nombre de fois que l’évènement (l’application du facteur multiplicatif) se produit dans la période donnée (déterminée en fonction de |x|).
L'évènement se produit plusieurs fois dans la période donnée.
L’évènement se produit tous les 3 mois et la variable |x| est en année. Il y a 4 évènements par période d’un an.||b=4||

L’évènement prend plus d’une période pour se produire.
L’évènement se produit tous les 5 ans et la variable |x| est en année. Il y a 1 évènement aux 5 ans.||b=\dfrac{1}{5}||

Pour résoudre un problème impliquant la fonction exponentielle, on doit résoudre une équation ou une inéquation exponentielle.
Jeanne s'est acheté une superbe voiture électrique neuve d'une valeur de |45\ 000\ $.| Les spécialistes en assurance automobile estiment qu'une voiture électrique perd en moyenne |20\ \%| de sa valeur chaque année. Sachant cela, quelle sera la valeur de la voiture de Jeanne dans |8| ans?
-
Identifier les variables
|x :| Temps écoulé (en années) depuis que Jeanne a acheté sa voiture
|f(x) :| Valeur ($) de la voiture -
Déterminer la règle
-
Déterminer la valeur de |\boldsymbol{a}|
C’est le prix d’achat de la voiture.||a=45\ 000|| -
Déterminer la valeur de |\boldsymbol{c}|
Si la voiture perd |20\ \%\ (0{,}2)| de sa valeur à chaque année, on a |1-0{,}2=0{,}8.|||c=0{,}8|| -
Déterminer la valeur de |\boldsymbol{b}|
L’évènement se reproduit une fois par an et la variable |x| est en nombre d’années.||b=\dfrac{\color{#333fb1}1}{\color{#EC0000}1}=1||
La règle de la fonction exponentielle est |f(x)=45\ 000(0{,}8)^x.|
-
-
Répondre à la question
On cherche la valeur de la voiture de Jeanne dans |8| ans. On remplace donc |x| par |8| et on trouve la valeur de |f(8).|||\begin{align}f(x)&=45\ 000(0{,}8)^{x}\\f(8)&=45\ 000(0{,}8)^8\\&\approx7\ 549{,}75\ $\end{align}||Ainsi, après |8| ans, la valeur de la voiture électrique de Jeanne sera approximativement de |7\ 549{,}75\ $.|
Il est possible de changer les unités de la variable |x| dans un problème. On doit toutefois s’assurer de faire les modifications dans la règle.
Dans l’exemple précédent, on aurait pu choisir de travailler en mois plutôt qu’en années. L’évènement se produit toujours une fois par an, donc une fois tous les |12| mois. On aurait alors eu que |b=\dfrac{1}{12}.| Pour répondre à la question, puisqu’on demandait la valeur dans |8| ans, il aurait fallu remplacer |x| par |96| mois. La réponse aurait alors été la même.
Il est possible de trouver la règle de l’exemple précédent en utilisant une table de valeurs. On sait que le prix d’achat est de |45\ 000\ $| et que, chaque année, elle ne conserve que |80\ \%| de sa valeur de l’année précédente.
| |\boldsymbol{x :}| Temps écoulé depuis que Jeanne a acheté sa voiture (années) | |\boldsymbol{f(x) :}| Valeur de la voiture ($) | |
|---|---|---|
|
|0| |
|45\ 000| |
|45\ 000| |
|
|1| |
|\color{#3a9a38}{45\ 000}\times 0{,}8| |
|45\ 000\times(0{,}8)^1| |
|
|2| |
|\color{#3a9a38}{45\ 000\times 0{,}8}\times 0{,}8| |
|45\ 000\times(0{,}8)^2| |
|
|3| |
|\color{#3a9a38}{45\ 000\times 0{,}8\times 0{,}8}\times 0{,}8| |
|45\ 000\times(0{,}8)^3| |
|
... |
... |
... |
|
|x| |
|\color{#3a9a38}{45\ 000\ \times\ }\underbrace{\color{#3a9a38}{0{,}8\times0{,}8\times\ldots}\times0{,}8}_{x\text{ fois}}| |
|45\ 000\times(0{,}8)^x| |
Le tableau permet de déterminer que la règle de la fonction est |f(x)=45\ 000(0{,}8)^x.|
Au début d'une expérience, un chercheur possède |50\ \text{g}| d'un élément radioactif. Cet élément se désintègre de sorte que sa masse diminue de moitié, |3| fois par heure. Quelle est la règle de la fonction exponentielle qui représente cette situation?
-
Identifier les variables
|x :| Temps écoulé (en heures) depuis le début de l'expérience
|f(x) :| Masse (en grammes) de l'élément radioactif -
Déterminer la règle de la fonction
-
Déterminer la valeur de |\boldsymbol{a}|
Puisque le chercheur possède |50\ \text{g}| de la substance au début de l’expérience, |50| est la valeur initiale.||a=50|| -
Déterminer la valeur de |\boldsymbol{c}|
Puisque la masse de l’élément radioactif diminue de moitié à chaque période, le facteur multiplicatif est |\dfrac{1}{2}.|||c=\dfrac{1}{2}|| -
Déterminer la valeur de |\boldsymbol{b}|
Comme |x| est un nombre d’heures, on doit se demander combien de fois l’évènement se produit par heure. On indique que l’élément radioactif diminue |\color{#333fb1}3| fois par heure.||b=\dfrac{\color{#333fb1}3}{\color{#EC0000}1}=3||
-
-
Répondre à la question
Ainsi, la règle de la fonction exponentielle représentée par cette situation est |f(x)=50\left(\dfrac{1}{2}\right)^{3x}.|
À |8\ \text{h}| ce matin, un échantillon de yogourt contenait |10\ 000| bactéries. À la température de la pièce, le nombre de bactéries présentes dans cet échantillon quadruple toutes les |2| heures. Si on considère que le yogourt n'est plus comestible à partir du moment où il contient |640\ 000| bactéries et plus, après combien d'heures cela se produira-t-il?
-
Identifier les variables
|x :| Temps (en heures) écoulé depuis |8\ \text{h}| ce matin
|f(x) :| Nombre de bactéries présentes dans l'échantillon de yogourt -
Déterminer la règle
-
Déterminer la valeur de |\boldsymbol{a}|
À |8\ \text{h}| ce matin (à |x=0|), le nombre de bactéries était de |10\ 000.|||a=10\ 000|| -
Déterminer la valeur de |\boldsymbol{c}|
Puisque le nombre de bactéries quadruple à chaque période, le facteur multiplicatif est |4.|||c=4|| -
Déterminer la valeur de |\boldsymbol{b}|
Comme |x| est un nombre d’heures, on doit se demander combien de fois l’évènement se produit par heure. On indique que les bactéries se multiplient |\color{#333fb1}1| fois toutes les |\color{#EC0000}2| heures.||b=\dfrac{\color{#333fb1}1}{\color{#EC0000}2}||
La règle de la fonction exponentielle est |f(x)=10\ 000 (4)^{\!^{\large\frac{x}{2}}}.|
-
-
Répondre à la question
On veut savoir après combien d’heures le nombre de bactéries dépasse |640\ 000.| On cherche donc la solution de l’inéquation suivante.||10\ 000 (4)^{\!^{\large\frac{x}{2}}}>640\ 000||On remplace le symbole |>| par un |=| et on résout l'équation.||\begin{align}10\ 000 (4)^{\!^{\large\frac{x}{2}}}&=640\ 000\\(4)^{\!^{\large\frac{x}{2}}}&=64\end{align}||On passe à la forme logarithmique pour isoler |x|.||\begin{align}\dfrac{x}{2}&=\log_4 64\\\dfrac{x}{2}&=3\\x&=6\end{align}||Ainsi, comme le nombre de bactéries dans le yogourt augmente, celui-ci devrait être jeté à la poubelle après |6| heures.
Il existe un cas particulier de fonction exponentielle à analyser : celui des placements ou des emprunts avec intérêts en mathématiques financières. Les paramètres |a| et |b| ont toujours la même signification. Par contre, si les intérêts sont composés annuellement ou à une autre fréquence, cela a une influence sur la valeur du paramètre |c.|
||\begin{align}f(x)&=a(c)^{bx}\\
f(x)&=a\left(1\pm\dfrac{i}{b}\right)^{bx}\end{align}||où
|a :| Valeur initiale
|c :| Facteur multiplicatif (lié au taux d’intérêt)
|b :| Nombre de fois par période donnée pour lequel les intérêts sont calculés
|i :| Taux d'intérêt (en nombre décimal)
On utilise le symbole |+| s'il y a un gain et le symbole |-| s’il y a une perte.
Après avoir obtenu un emploi étudiant et avoir travaillé tout l'été, Alexandre a réussi à économiser |4\ 000\ $.| Il place ce montant à un taux d’intérêt annuel de |3\ \%| composé mensuellement. Après combien de temps son placement atteindra-t-il une valeur de |6\ 000\ $|?
-
Identification des variables
|x :| Temps écoulé (en années) depuis qu'Alexandre a placé ses économies
|f(x) :| Valeur de ses économies |($)| -
Déterminer la règle
-
Déterminer la valeur de |\boldsymbol{a}|
Le montant initial est de |4\ 000\ $.|||a=4\ 000|| -
Déterminer le paramètre |\boldsymbol{c}|
Comme il s’agit d’un taux d’intérêt de |3\ \%\ (0{,}03)| composé chaque mois (|12| mois dans une année) et que c’est une valeur qui s’ajoute chaque période, on obtient ceci.||\begin{align}c&=1+\dfrac{0{,}03}{12}\\&=1{,}002\,5\end{align}|| -
Déterminer la valeur de |\boldsymbol{b}|
La variable |x| est en années, mais les intérêts se composent chaque mois. Les intérêts se composent donc |\color{#333fb1}{12}| fois dans |\color{#ec0000}1| année.||b=\dfrac{\color{#333fb1}{12}}{\color{#EC0000}1}=12||
La règle de la fonction est |f(x)=4\ 000(1{,}002\,5)^{12x}.|
-
-
Répondre à la question
On cherche à quel moment la valeur du placement atteindra |6\ 000\ $.| On remplace donc |f(x)| par |6\ 000| et on isole |x.|||\begin{align}6\ 000&=4\ 000(1{,}002\,5)^{12x}\\1{,}5&=(1{,}002\,5)^{12x}\end{align}||On passe à la forme logarithmique et on trouve la valeur de |x| en effectuant un changement de base. ||\begin{align}12x&=\log_{1{,}002\,5}1{,}5\\12x&=\dfrac{\log1{,}5}{\log{1{,}002\,5}}\\12x&\approx162{,}39\\x&\approx13{,}53\end{align}||Ainsi, le placement d'Alexandre aura atteint une valeur de |6\ 000\ $| après environ |13| ans et demi.
Pour valider ta compréhension à propos de la résolution de problèmes impliquant la fonction exponentielle de façon interactive, consulte la MiniRécup suivante.
