To subtract fractions with common denominators, you simply subtract the numerators and keep the same denominator for the answer.
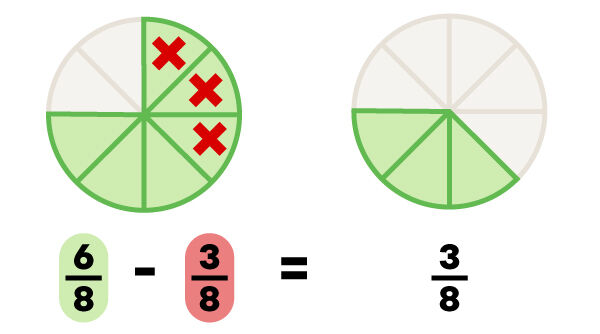
When the fractions have different denominators, you have to find a common denominator and then convert the fractions so they remain equivalent.
To subtract fractions when the denominator of one is a multiple of the other, follow these steps.
-
I identify the fraction with the smallest denominator.
-
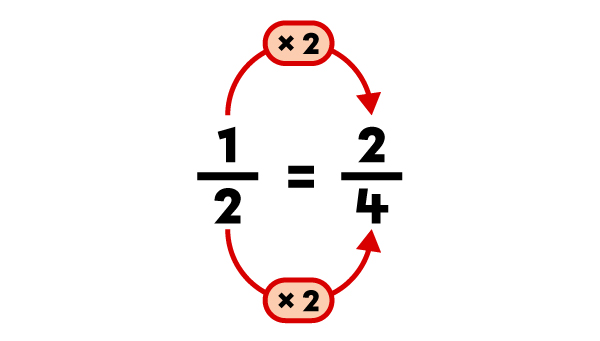
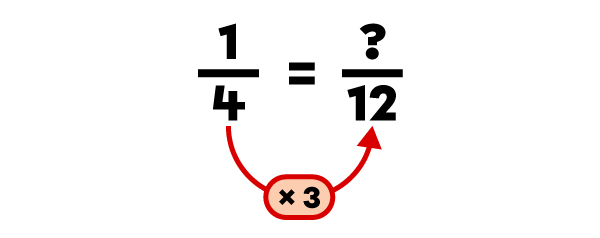
I find the number to multiply the denominator by in order to get the same denominator as the other fraction.
-
I multiply the numerator by the same number.
-
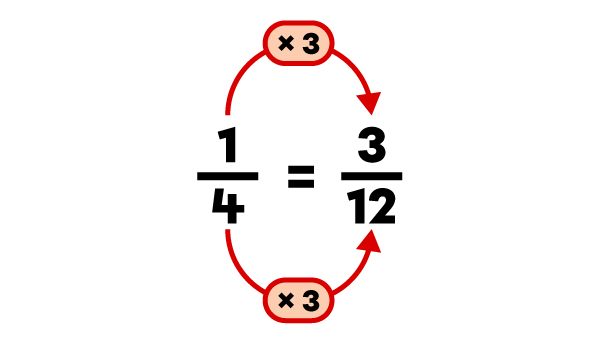
I rewrite the subtraction with the converted fraction.
-
I subtract the numerators only.
-
I write the answer using the same denominator as the subtracted fractions.
Make sure to read the given instructions carefully because sometimes the answer may have to be expressed as a mixed number or as an irreducible fraction.
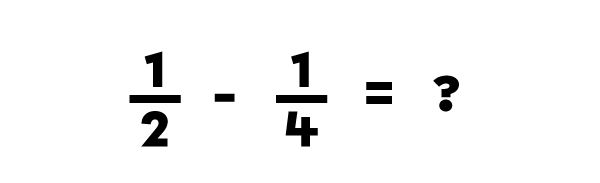
|
 |
|
 |
|
 |
|
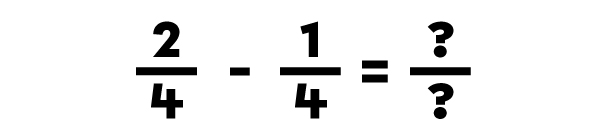 |
|
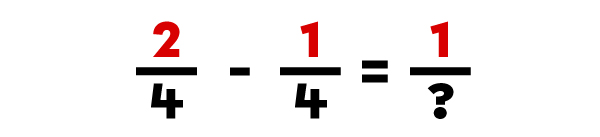 |
|
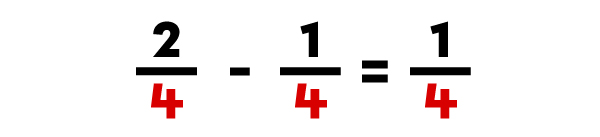 |
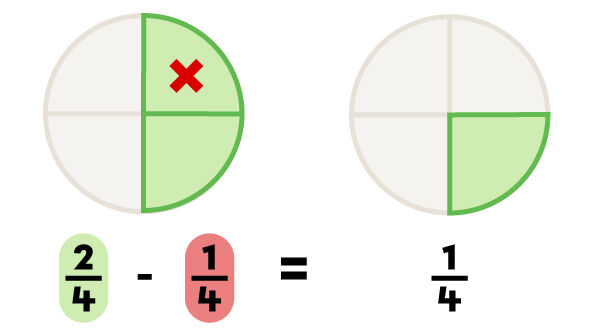
When the fractions have different denominators, you have to find a common (identical) denominator and then convert the fractions so that they stay equivalent.
To subtract fractions with different denominators using the LCM, follow these steps.
-
I find the least common multiple (LCM) of the denominators.
-
I find the number to multiply the denominator of the fraction by to get the LCM.
-
I multiply the numerator of the fraction by the same number.
-
I rewrite the subtraction with the converted fractions.
-
I subtract the numerators only.
-
I write in the answer using the same denominator as the subtracted fractions.
Make sure to read the given instructions carefully because sometimes the answer may have to be expressed as a mixed number or as an irreducible fraction.
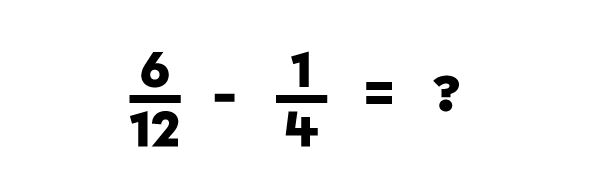
|
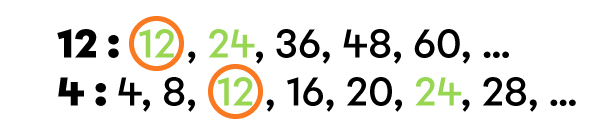 |
|
 |
|
 |
|
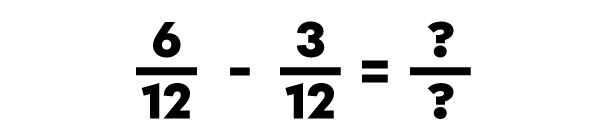 |
|
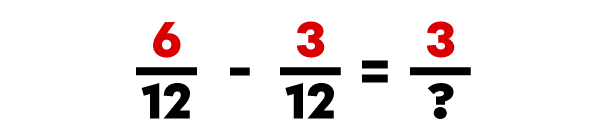 |
|
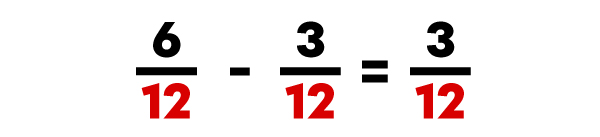 |
