When we classify the elements of a sample space in a Venn diagram, we are often interested in the intersection |(\cap)| or the union |(\cup)| of two sets. This leads to the calculation of probabilities.
In the following interactive animation, you can see a Venn diagram with two sets (A and B). You can check the box to see a 3rd set (C) if you wish. Next, you can observe the intersections of the different sets, which will appear shaded, or observe the different possible unions.
The intersection of sets, denoted by the symbol |\cap|, includes the elements common to all the studied sets. It is associated with the notion of "and" in probability.
In a Venn diagram, the intersection of the sets |A| and |B,| denoted |A \cap B,| is the area in the centre of the diagram whose elements belong to both set |A| and set |B.|
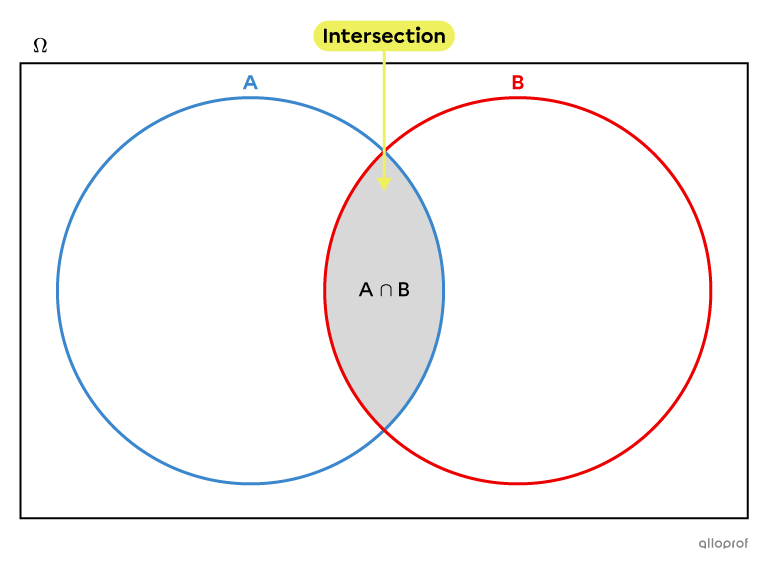
In a 3-set Venn diagram, the intersection of the sets |A,| |B| and |C,| denoted |A\cap B\cap C,| is the area in the centre of the diagram whose elements are simultaneously part of set |A,| set |B| and set |C|.
Consider the 2 following sets.
|A :| Odd numbers less than |10|
|B :| Multiples of |3| less than |10|
Here is a list of the elements of each of these sets.
|A= \{1, \color{#3a9a38}{3}, 5, 7, \color{#3a9a38}{9} \}|
|B = \{\color{#3a9a38}{3}, 6, \color{#3a9a38}{9} \}|
The numbers |\color{#3a9a38}{3}| and |\color{#3a9a38}{9}| are common to both sets since they are both odd numbers and multiples of |3| less than |10.| The intersection of the sets |A| and |B| can be written like so. ||A \cap B = \{3, 9\}||
By representing the sets |A| and |B| in a Venn diagram where the sample space |(\Omega)| corresponds to the set of numbers less than |10,| we notice that the numbers |3| and |9| are indeed located in the area that is common to both sets |A| and |B.|

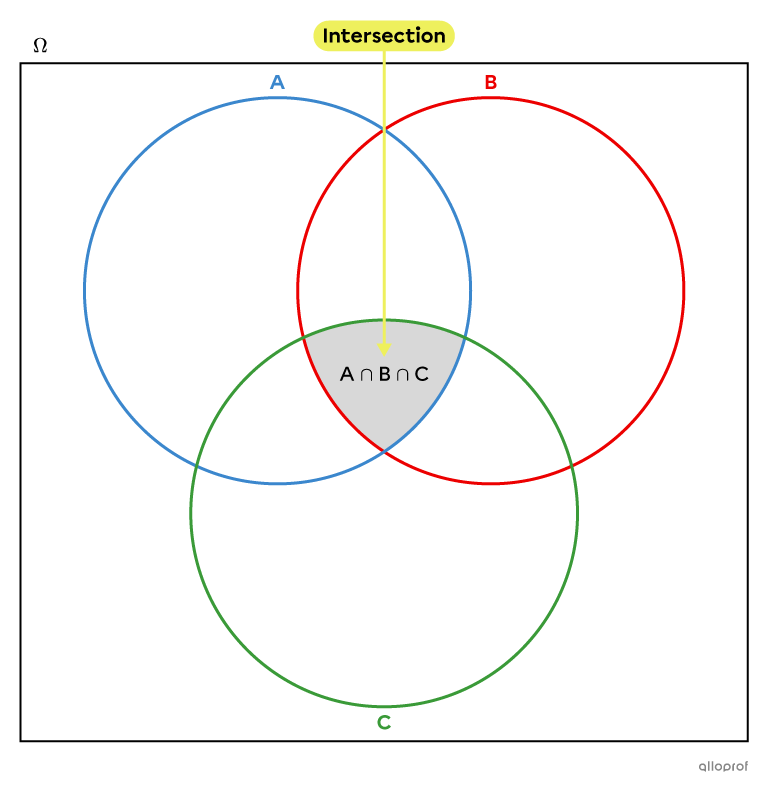
Consider the following 3 sets that are part of |\Omega=\{1, 2, 3, 4, 5, 6\}.|
|A :| Natural numbers less than |4|
|B :| Even numbers
|C :| The numbers between |1| and |7|
Here is the list of the elements of each of these sets.
|A = \{1, \color{#3a9a38}{2}, 3 \}|
|B = \{ \color{#3a9a38}{2}, 4, 6 \}|
|C = \{ \color{#3a9a38}{2}, 3, 4, 5, 6 \}|
We can represent them in the following Venn diagram.
The number |2| is the only element found in all 3 sets.
||A \cap B \cap C = \{2\}||
It is possible to focus on the intersections of the sets taken 2 by 2. We therefore obtain the following intersections. ||\begin{align}A \cap B &= \{2\}\\ A\cap C &= \{2, 3\}\\B\cap C &= \{2, 4, 6\} \end{align}||
Note: It is very possible that the intersection of 2 sets is identical to that of 3 sets, as is the case in this example: |A \cap B \cap C=A \cap B.|
It is possible for sets to have no elements in common. In this case, their intersection is in fact an empty set and the sets are said to be disjoint or incompatible.
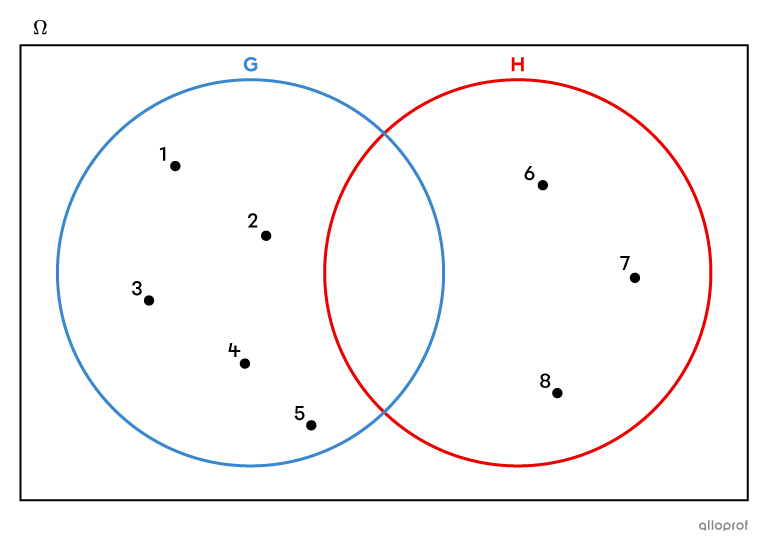
Consider the 2 following sets:
|G = \{1,2,3,4,5\}|
|H = \{6,7,8\}|
No number is common to both sets |G| and |H.| Their intersection is an empty set.
||G \cap H = \{\ \}\ \text{or}\ \varnothing||Therefore, sets |G| and |H| are incompatible (disjoint).
The intersection |(\cap)| of 2 sets |A| and |B| is expressed as follows: ||A \cap B = \lbrace x \in \Omega \mid x \in A \text{ and } x \in B \rbrace||
where
|\Omega :| the sample space
The union of 2 sets, denoted by the symbol |\cup,| is the set that contains all the elements that belong to each set or to both sets at once. The union is associated with the notion of "or" in probability.
In a Venn diagram, the union of the sets |A| and |B,| written as |A \cup B,| includes everything inside set |A| and set |B,| including the common part of both sets.
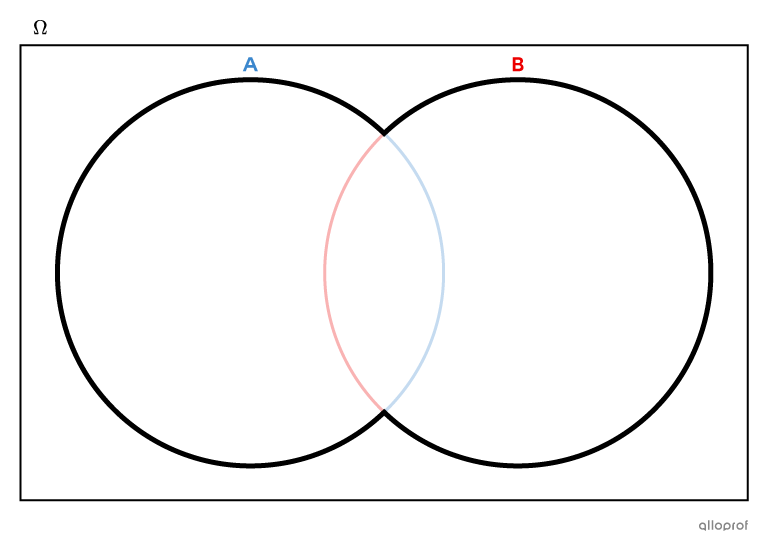
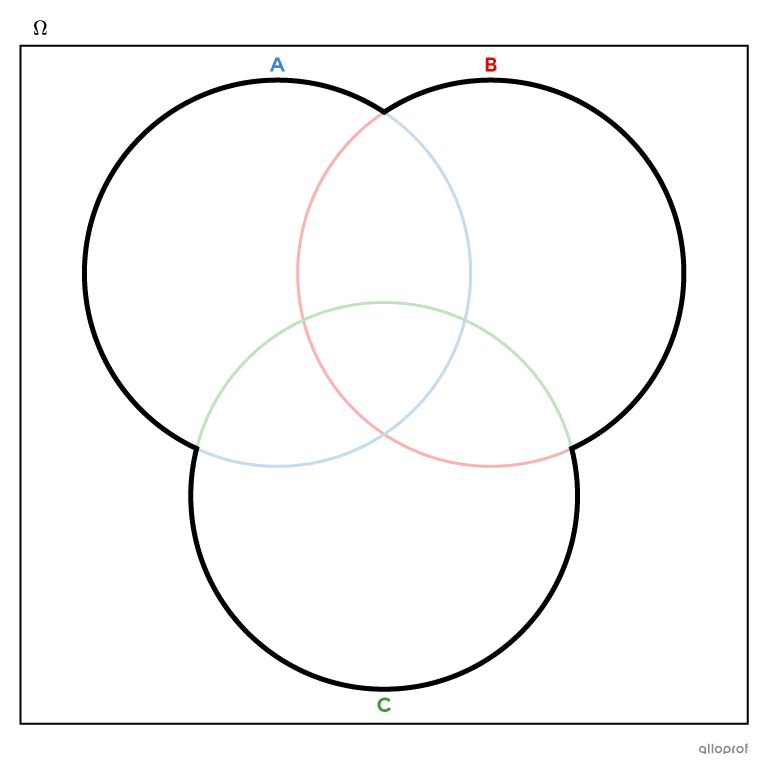
In a 3-set Venn diagram, the union of the sets |A,| |B| and |C,| written as |A\cup B\cup C,| includes everything that is located inside the 3 circles.
To find all the elements of the union of |A| and |B|, or to enumerate sets |A| and |B,| we use the following formula.
Elements of |A\cup B =| Elements of |A +| Elements of |B -| The elements of their intersection
||A\cup B = A + B - (A\cap B)||
It is possible to use a similar formula to calculate the probability of choosing a random number from the intersection of 2 sets.
||P(A\cup B) = P(A) + P(B) - P(A\cap B)||
Consider the natural numbers less than |10| included in the following sets |A| and |B.|
|A :| The factors of |12|
|B :| The multiples of |3|
a) What elements belong to the union of sets |A| and |B|?
b) How many elements are there in the union of these sets?
c) What is the probability that a randomly chosen natural number less than |10| belongs to the union of these sets?
-
Make a list of the elements of each set
||\begin{align}A &= \{1,2,3,4,6\} \\ B &= \{3, 6, 9\}\end{align}|| -
Fill in the Venn diagram
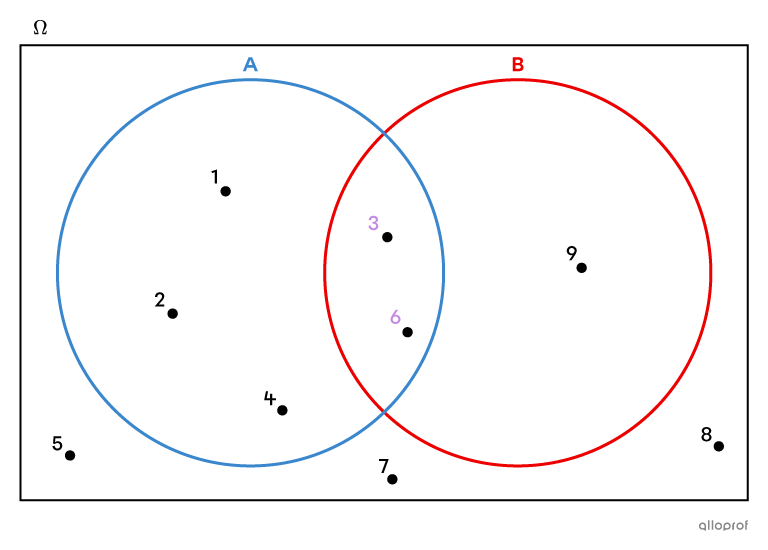
-
Determine the intersection of the 2 sets
The intersection of |A| and |B| is the following: ||A \cap B = \{ \color{#c58ae1}{3}, \color{#c58ae1}{6}\}|| -
Determine the union of the 2 sets by applying the appropriate formula
a)To determine the elements included in the union of the 2 sets, we use the following procedure.||\begin{align}A \cup B &=\color{#3b87cd}A\quad+\quad \color{#ec0000}B\quad-\quad\color{#c58ae1}{(A\cap B)}\\ &= \{1, 2, \color{#c58ae1}3, 4, \color{#c58ae1}6 \} + \{\color{#c58ae1}3, \color{#c58ae1}6, 9 \} - \{\color{#c58ae1}3, \color{#c58ae1}6\} \\ &= \{1, 2, 3, 4, 6, 9\} \end{align}||
b)To enumerate the union of the 2 sets, we proceed with the following calculation. ||\begin{align}A \cup B &=\color{#3b87cd}A+ \color{#ec0000}B-\color{#c58ae1}{A\cap B}\\ &=\, \color{#3b87cd}5\, + \,\color{#ec0000}3 -\, \color{#c58ae1}{2} \\ &=\, 6 \ \text{elements}\end{align}||
c)To calculate the probability that a natural number less than |10| chosen at random is a divisor of |12| or a multiple of |3,| we perform the following calculation. ||\begin{align}P(A\cup B) &=P(\color{#3b87cd}A)+P( \color{#ec0000}B)-P(\color{#c58ae1}{A\cap B})\\ &=\ \ \dfrac{\color{#3b87cd}5}{9}\quad +\ \ \dfrac{\color{#ec0000}3}{9}\quad -\ \ \dfrac{\color{#c58ae1}{2}}{9} \\ &=\ \ \dfrac{6}{9}\end{align}||
When the intersection of 2 sets is empty and the union of the 2 sets corresponds to the entire sample space, we can say that the sets are complementary.
The union of the sets |A| and |B| is written in the following manner. ||A \cup B = \lbrace x \in \Omega \mid x \in A \text{ or } x \in B \rbrace||
where
|\Omega:| sample space
|
|
||
|---|---|---|
|
||A \cap B = B \cap A|| |
||A \cup B = B \cup A|| |
|
|
||(A \cap B)\cap C = A\cap (B \cap C)|| |
||(A \cup B)\cup C = A\cup (B \cup C)|| |
|
|
The intersection distributes over the union. |
The union distributes over the intersection. |