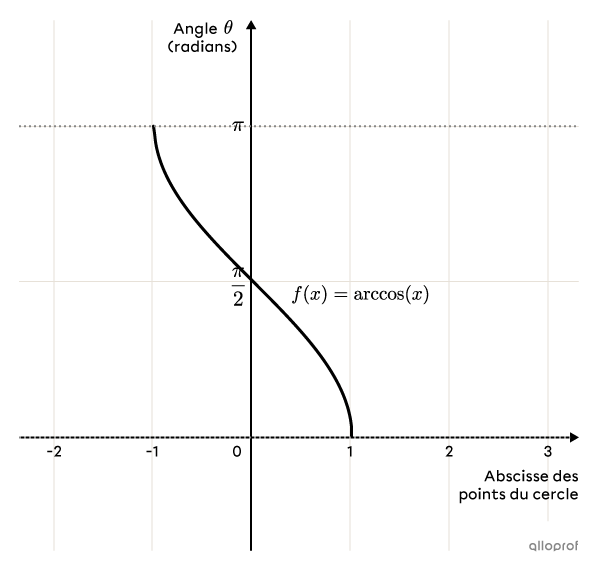
La réciproque de la fonction cosinus de base est la fonction arc cosinus qui s'intéresse à la mesure des angles (en radians) du cercle trigonométrique en fonction de l’abscisse des points du cercle.
La règle de la fonction arc cosinus de base est |f(x)=\arccos (x).| On note aussi cette fonction |f(x)=\cos^{-1}(x).|
Remarque : Il ne faut pas confondre la notation |\cos^{-1}(x)| avec |\dfrac{1}{\cos (x)}.|
Voici un résumé des propriétés de la fonction |\arccos.|
-
Le domaine de la fonction est |[-1,1].|
-
L’image (codomaine) est |[0, \pi].|
-
L’ordonnée à l’origine est |\dfrac{\pi}{2}.|
-
L’abscisse à l’origine est |1.|
-
La fonction est décroissante sur son domaine.
-
La fonction est positive sur son domaine.
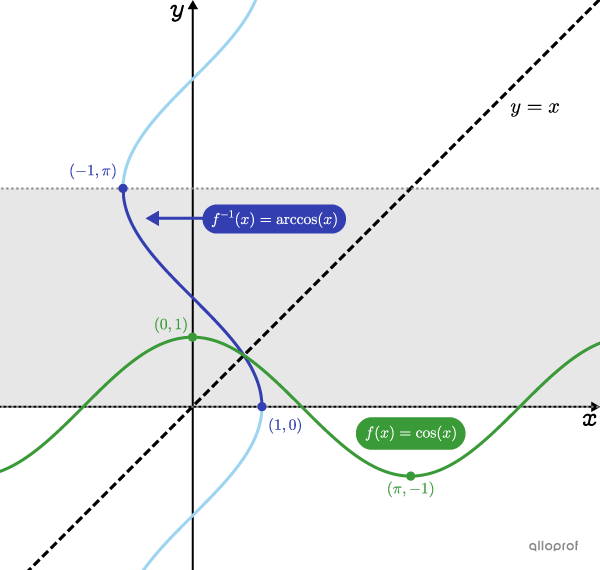
La réciproque d’une fonction cosinus n’est pas une fonction. Pour qu’elle le devienne, on doit restreindre son image.
Dans le plan cartésien ci-dessous, on a tracé la fonction cosinus de base. Pour tracer sa réciproque, on interchange les coordonnées |x| et |y| des points de la fonction. On peut aussi effectuer une réflexion des points par rapport à la droite d’équation |y=x.| Par exemple, le point |(0,1)| devient le point |(1,0).|
En procédant ainsi, on obtient une autre courbe, qui n’est pas une fonction. En limitant l’image de la réciproque à l’intervalle |[0, \pi],| on obtient la fonction arc cosinus.
Pour trouver la règle de la réciproque d’une fonction cosinus, on suit les étapes suivantes.
-
Interchanger |x| et |y| dans la règle.
-
Isoler la variable |y.|
-
Donner la règle de la réciproque.
Détermine la règle de la réciproque de la fonction |f(x)=3\cos\left(-\dfrac{2}{5}(x+\pi)\right)+1.|
-
Interchanger |x| et |y| dans la règle ||\begin{align}\color{#3B87CD}y&=3\cos\left(-\dfrac{2}{5}(\color{#FF55C3}x+\pi)\right)+1\\ \color{#FF55C3}x&=3\cos\left(-\dfrac{2}{5}(\color{#3B87CD}y+\pi)\right)+1\end{align}||
-
Isoler la variable |y|
||\begin{align}x&=3\cos\left(-\dfrac{2}{5}(\color{#3B87CD}y+\pi)\right)+1\\x-1&=3\cos\left(-\dfrac{2}{5}(\color{#3B87CD}y+\pi)\right)\\ \dfrac{x-1}{3}&=\cos\left(-\dfrac{2}{5}(\color{#3B87CD}y+\pi)\right)\end{align}||Pour isoler |y,| il faut éliminer |\cos| en effectuant l’opération inverse, |\cos^{-1}.|
||\begin{align}\color{#EC0000}{\cos^{-1}\!\left(\color{black}{\dfrac{x-1}{3}}\right)}&=-\dfrac{2}{5}(\color{#3B87CD}y+\pi)\\-\dfrac{5}{2}\cos^{-1}\!\left(\dfrac{x-1}{3}\right)&=\color{#3B87CD}y+\pi\\-\dfrac{5}{2}\cos^{-1}\!\left(\dfrac{x-1}{3}\right)-\pi&=\color{#3B87CD}y\end{align}||
Il est possible de simplifier l’écriture en travaillant dans les parenthèses. En effet, la division par |3| peut aussi s’écrire comme une multiplication par |\dfrac{1}{3}.|||\begin{align}-\dfrac{5}{2}\cos^{-1}\!\left(\color{#EC0000}{\dfrac{x-1}{3}}\right)-\pi&=y\\ -\dfrac{5}{2}\cos^{-1}\!\left(\color{#EC0000}{\dfrac{1}{3}(x-1)}\right)-\pi&=y\end{align}||
-
Donner la règle de la réciproque
La règle de la réciproque de la fonction cosinus est la suivante.
||f^{-1}(x)=-\dfrac{5}{2}\cos^{-1}\!\left(\dfrac{1}{3}(x-1)\right)-\pi||
Remarque : Pour que la réciproque devienne une fonction, on doit limiter son image.
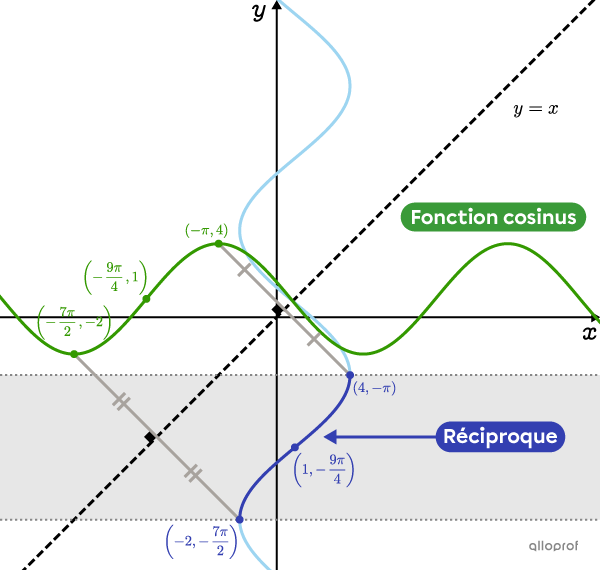
Voici la représentation graphique de la fonction cosinus de l’exemple précédent, dont la règle est |f(x)=3\cos\left(-\dfrac{2}{5}(x+\pi)\right)+1.|
Afin que la réciproque puisse devenir une fonction, on limite son image. Dans cet exemple, on doit limiter l’image à l’intervalle |\color{#333fb1}{\left[-\dfrac{7\pi}{2},-\pi\right]}.|