The inverse variation function (or an inversely proportional situation) is a function where at any point |(x,y),| the product of |x \times y| is constant.
The rule of an inverse variation function is ||y=\dfrac{k}{x}||where |x > 0.|
We often associate the inverse variation function with rational functions. The rule of a rational function is the following:
||f(x)=\dfrac{a}{b(x-h)}+k||
where |x \neq h|
The inverse variation function is considered a special case of the rational function. The product of the |x| and |y| variables are not necessarily constant in rational functions, unlike inverse variation functions.
For any point |(x,y)| of an inverse variation function, when we multiply |x| and |y,| we always obtain the same value. The value is called the constant product, which is usually denoted by the letter |k.| Simply determine the value of parameter |k| to find the rule of an inverse variation function.
Consider the following table of values.
| |x| | |y| | |x\times y=\color{#ec0000}{k}| |
|---|---|---|
| |1| | |320| | |1\times 320 = \color{#ec0000}{320}| |
| |2| | |160| | |2 \times 160 = \color{#ec0000}{320}| |
| |4| | |80| | |4\times 80 = \color{#ec0000}{320}| |
| |5| | |64| | |5\times 64 = \color{#ec0000}{320}| |
| |8| | |40| | |8\times 40 = \color{#ec0000}{320}| |
| |10| | |32| | |10 \times 32 = \color{#ec0000}{320}| |
| |16| | |20| | |16 \times 20 = \color{#ec0000}{320}| |
| |20| | |16| | |20 \times 16 = \color{#ec0000}{320}| |
| |32| | |10| | |32 \times 10 = \color{#ec0000}{320}| |
| |40| | |8| | |40\times 8 = \color{#ec0000}{320}| |
The product of |x| and |y| is always |320,| which means that it is an inverse variation function.
Therefore, the rule associated with the table of values is |y=\dfrac{320}{x}.|
-
Choose a point |(x,y).|
-
Replace |x| and |y| in the formula |y= \dfrac{k}{x}| with the chosen coordinates.
-
Isolate |k.|
Find the rule for the inverse variation function with the following graph.

-
Choose a point
We choose the point |(2,5)| -
Replace |x| and |y|
Replacing |x| with |2| and |y| with |5,| we obtain:
||\begin{align} y&=\dfrac{k}{x}\\ \color{#3b87cd}{5}&=\dfrac{k}{\color{#3b87cd}{2}} \end{align}|| -
Isolate |k|
Using cross-multiplication: ||\begin{align} \color{#3b87cd}{2}\times \color{#3b87cd}{5} &= k \\ 10 &=k \end{align}||
The rule for the inverse variation function is |y= \dfrac{10}{x}|
It’s possible to select another point to confirm your equation is correct.
For word problems, a few clues indicate the problem involves an inversely proportional situation:
-
The value of the dependent variable |(y)| decreases as the independent variable |(x)| increases.
-
The problem often describes a situation where something must be divided into equal parts. For instance, one or more of the following words are used: shared, divided, equally portioned, separated into equal parts, etc.
When a word problem suggests an inversely proportional situation, it is best to produce a table of values to analyze the variation of the function.
Louis decides to rent a cottage in the Laurentians to celebrate his birthday. He invites several of his friends to a party. The cost of renting the cottage is |$\ 480| for the weekend. Louis’ friends decide to split the cost of the cottage evenly. Louis wants to know how much each person will have to pay, based on the total number of people who show up.
When |1| person rents the cottage, it costs |$\ 480.| When |2| people rent the cottage, it costs each person |$\ 240.| Following the pattern, we end up with the following table of values.
| |x:| Number of people | |y:| Cost per person |($)| |
|---|---|
| |1| | |480| |
| |2| | |240| |
| |3| | |160| |
| |4| | |120| |
| |5| | |96| |
| |6| | |80| |
| |8| | |60| |
| |10| | |48| |
| |15| | |32| |
| |20| | |24| |
| |30| | |16| |
| |40| | |12| |
-
Choose a point
Let’s choose the point |(10,48)| -
Replace |x| and |y|
Replacing |x| with |10| and |y| with |48,| we obtain:
||\begin{align}y &= \dfrac{k}{x} \\ 48 &= \dfrac{k}{10}\end{align}|| -
Isolate |k|
||\begin{align} 48\times 10 &= k \\ 480 &=k \end{align}||
Therefore, the rule of the inverse variation function for the cost |($)| each person will have to pay according to the number of people is:
|y= \dfrac{480}{x}.|
To graph an inverse variation function in the form of |y= \dfrac{k}{x},| we create a table of values by trying out different |x| values and calculating the corresponding |y| values from the given equation.
Sketch the graph associated with the rule |y=\dfrac{24}{x}.|
Construct a table of values from the equation:
| |x| | |y| |
|---|---|
| |1| | |24| |
| |2| | |12| |
| |3| | |8| |
| |4| | |6| |
| |5| | |\dfrac{24}{5}| |
The following is the graph of the inverse variation function.
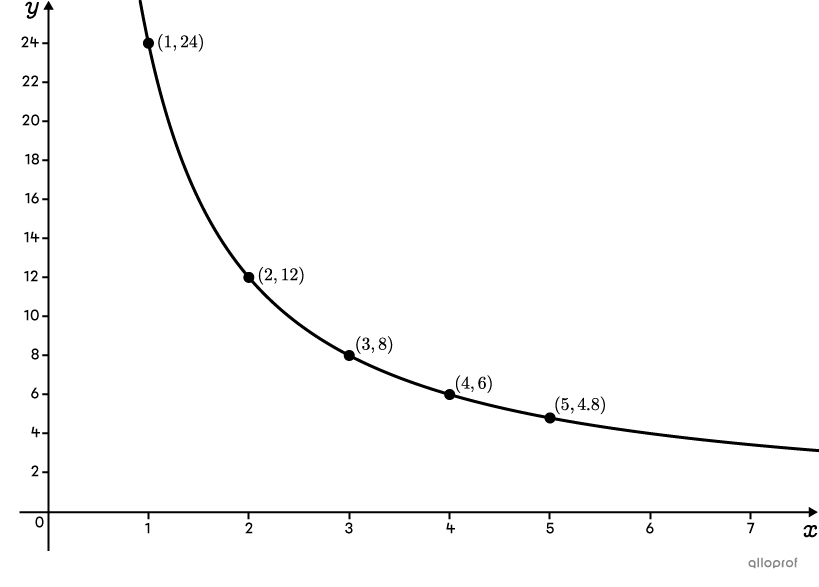
As we saw in the previous example, the graph of an inverse variation function is a curve that slowly decreases. Also, the curve approaches both axes, without ever touching them (meaning the axes are asymptotes).
- The curve intersects the points |(1,k)| and |(k,1).|
- The domain is |]0,+\infty[.|
- The range is |]0,+\infty[.|
- The function is decreasing over its entire domain.
- The function has no |y|-intercept and no zeros.
- The function has no maximum or minimum.
- The function has 2 asymptotes: |x=0| and |y=0.|
- The function is positive over its domain.
-
If parameter |k| is greater than |1| |(k>1),| the curve stays farther away from the origin.
-
If parameter |k| is between |0| and |1| |(0<k<1),| the curve comes closer to the origin.
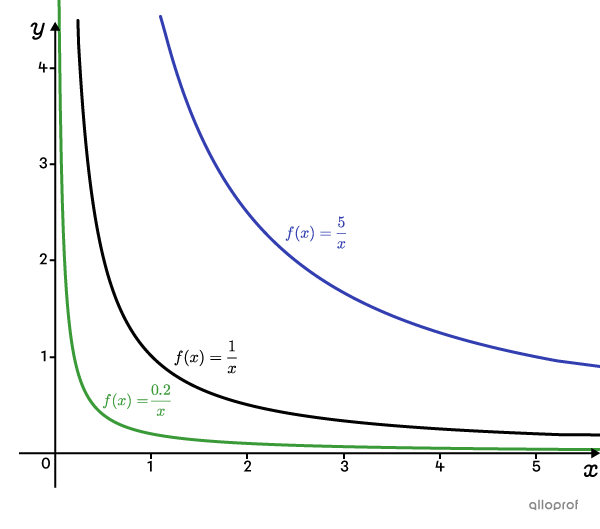
To obtain the inverse of an inverse variation function, we must interchange the dependent and independent variables.
The following rule represents the number of croissants |(n),| that can be bought with |\$6,| in relation to the price in |\$| of one croissant |(p):|
||n=\dfrac{6}{p}||
What is the rule of the inverse, in other words, the rule that represents the price of one croissant in relation to the number of croissants purchased with |\$6?|
The inverse rule is obtained by simply interchanging the variables |n| and |p.|
||\begin{align} \color{#3B87CD}n &= \dfrac{6}{\color{#FF55C3}p} \\ \color{#FF55C3}p &= \dfrac{6}{\color{#3B87CD}n} \end{align}||
Answer: The rule of the inverse is |p= \dfrac{6}{n}.|
Note: The graphs of the inverse variation function and its inverse are identical. Each point of the inverse is obtained by interchanging the coordinates of the points of the original function.

The point |(2,3)| indicates that when the price of a croissant is |\$2,| we can buy |3| croissants with a budget of |\$6.|
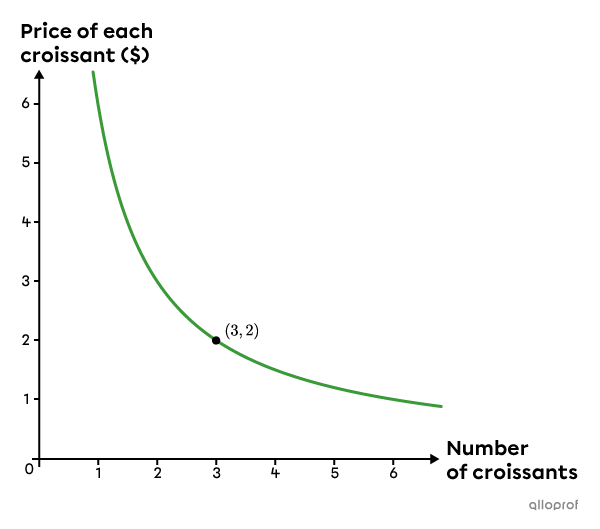
The point |(3,2)| indicates that when |3| croissants are bought with |\$6,| each croissant costs |\$2|.
Pour valider ta compréhension à propos des situations de proportionnalité et des situations inversement proportionnelles de façon interactive, consulte la MiniRécup suivante :
