La fonction de variation inverse, aussi appelée situation inversement proportionnelle, est une fonction dont le produit |x \times y| est constant pour tout couple |(x,y).|
La règle d'une fonction de variation inverse est la suivante. ||y=\dfrac{k}{x}||où |x > 0|
On associe souvent la fonction de variation inverse à la fonction rationnelle. La règle sous la forme canonique d’une fonction rationnelle est la suivante.||f(x)=\dfrac{a}{b(x-h)}+k||
où |x \neq h|
Autrement dit, on peut considérer que la fonction de variation inverse est un cas particulier de l’ensemble des fonctions rationnelles. Dans le cas des fonctions rationnelles, le produit des variables |x| et |y| n’est pas nécessairement constant, contrairement aux fonctions de variation inverse.
Pour tout couple |(x,y)| d’une situation inversement proportionnelle, lorsqu’on multiplie |x| et |y,| on obtient toujours la même valeur. Cette valeur se nomme le produit constant, lequel est généralement désigné par la lettre |k.| Il suffit donc de déterminer la valeur du paramètre |k| pour trouver la règle d’une fonction de variation inverse.
Soit la table de valeurs suivante.
| |x| | |y| | |x\times y=\color{#ec0000}{k}| |
|---|---|---|
| |1| | |320| | |1\times 320 = \color{#ec0000}{320}| |
| |2| | |160| | |2 \times 160 = \color{#ec0000}{320}| |
| |4| | |80| | |4\times 80 = \color{#ec0000}{320}| |
| |5| | |64| | |5\times 64 = \color{#ec0000}{320}| |
| |8| | |40| | |8\times 40 = \color{#ec0000}{320}| |
| |10| | |32| | |10 \times 32 = \color{#ec0000}{320}| |
| |16| | |20| | |16 \times 20 = \color{#ec0000}{320}| |
| |20| | |16| | |20 \times 16 = \color{#ec0000}{320}| |
| |32| | |10| | |32 \times 10 = \color{#ec0000}{320}| |
| |40| | |8| | |40\times 8 = \color{#ec0000}{320}| |
Le produit de |x| et |y| donne toujours |320,| ce qui implique qu’il s’agit d’une fonction de variation inverse.
La règle associée à cette table de valeurs est donc |y=\dfrac{320}{x}.|
-
Choisir un couple |(x,y).|
-
Remplacer |x| et |y| dans la formule |y= \dfrac{k}{x}| par les coordonnées choisies à l'étape 1.
-
Isoler |k.|
Trouve la règle de la fonction de variation inverse dont le graphique est le suivant.

-
Choisir un couple
On prend le couple |(2,5).| -
Remplacer |x| et |y|
En remplaçant |x| par |2| et |y| par |5| dans la formule, on obtient : ||\begin{align} y&=\dfrac{k}{x}\\ \color{#3b87cd}{5}&=\dfrac{k}{\color{#3b87cd}{2}} \end{align}|| -
Isoler |k|
On fait un produit croisé. ||\begin{align} \color{#3b87cd}{2}\times \color{#3b87cd}{5} &= k \\ 10 &=k \end{align}||
Réponse : La règle de la fonction de variation inverse est |y= \dfrac{10}{x}.|
On peut sélectionner un autre couple et vérifier si l’équation est correcte.
Dans un problème écrit, quelques indices permettent de savoir qu’il s’agit d’une situation inversement proportionnelle.
-
La valeur de la variable dépendante |(y)| diminue lorsque la valeur de la variable indépendante |(x)| augmente.
-
Le problème décrit souvent une situation dans laquelle on doit diviser un tout en parts égales. On peut retrouver, par exemple, un ou des mots parmi les suivants : partager, diviser, faire des portions équitables, séparer en parts égales, etc.
À partir d'un problème écrit impliquant une situation inversement proportionnelle, il est préférable de produire une table de valeurs pour bien analyser la variation de la fonction.
Louis décide de louer un chalet dans les Laurentides pour fêter son anniversaire. Il invite plusieurs de ses amis pour célébrer avec lui. Le cout de la location du chalet s’élève à |480\ $| pour la fin de semaine. Les amis de Louis décident de se partager entre eux le cout de la location du chalet.
Louis s’intéresse donc au cout que chaque personne aura à débourser selon le nombre de personnes qui seront présentes lors de cette fin de semaine.
Ainsi, si |1| personne loue le chalet, elle devra débourser |480\ $.| Si |2| personnes louent le chalet, chaque personne devra débourser |240\ $.| En poursuivant ce raisonnement, on peut produire la table de valeurs suivante.
| |x:| Nombre de personnes présentes | |y:| Cout par personne |($)| |
|---|---|
| |1| | |480| |
| |2| | |240| |
| |3| | |160| |
| |4| | |120| |
| |5| | |96| |
| |6| | |80| |
| |8| | |60| |
| |10| | |48| |
| |15| | |32| |
| |20| | |24| |
| |30| | |16| |
| |40| | |12| |
-
Choisir un couple
On prend le couple |(10,48).| -
Remplacer |x| et |y|
En remplaçant |x| par |10| et |y| par |48| dans la formule, on obtient :||\begin{align}y &= \dfrac{k}{x} \\ 48 &= \dfrac{k}{10}\end{align}|| -
Isoler |k| ||\begin{align} 48\times 10 &= k \\ 480 &=k \end{align}||
Ainsi, la règle de la fonction de variation inverse qui donne le cout |($)| que chacune des personnes aura à débourser en fonction du nombre de personnes présentes est |y= \dfrac{480}{x}.|
Pour tracer une fonction de variation inverse de la forme |y= \dfrac{k}{x},| on choisit différentes valeurs de |x| et on calcule les valeurs de |y| à partir de l'équation donnée.
Trace le graphique associé à la règle |y=\dfrac{24}{x}.|
On peut produire une table de valeurs à partir de cette équation.
| |x| | |y| |
|---|---|
| |1| | |24| |
| |2| | |12| |
| |3| | |8| |
| |4| | |6| |
| |5| | |\dfrac{24}{5}| |
Voici le graphique de cette fonction de variation inverse.
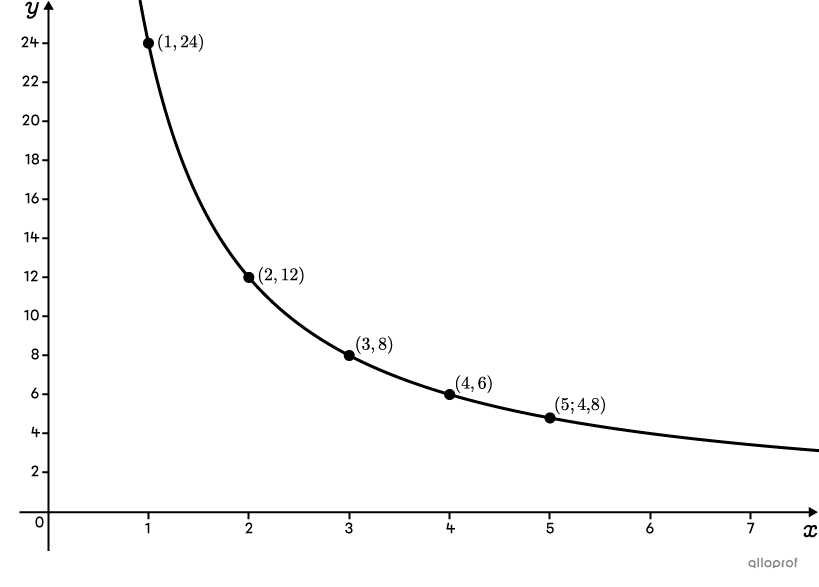
Comme on peut le voir dans l’exemple précédent, le graphique d’une fonction de variation inverse est composé d’une courbe qui décroit de moins en moins rapidement. Aussi, la courbe se rapproche des 2 axes du plan cartésien sans jamais y toucher.
-
La courbe passe par les points |(1,k)| et |(k,1).|
-
Le domaine est |]0,+\infty[.|
-
L’image est |]0,+\infty[.|
-
La fonction est décroissante sur son domaine.
-
La fonction ne possède pas d’ordonnée à l’origine ni de zéro.
-
La fonction ne possède pas de maximum ni de minimum.
-
La fonction possède 2 asymptotes : |x=0| et |y=0.|
-
La fonction est positive sur son domaine.
-
Si le paramètre |k| est plus grand que |1| |(k>1),| la courbe s'éloigne de l'origine.
-
Si le paramètre |k| est compris entre |0| et |1| |(0<k<1),| la courbe se rapproche de l'origine.
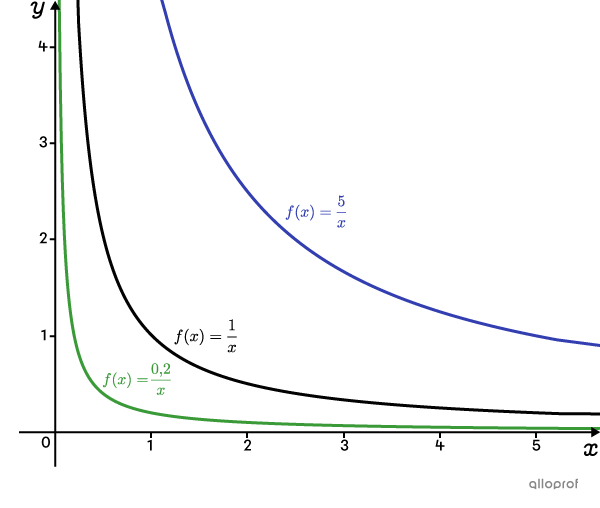
Pour obtenir la réciproque d’une fonction de variation inverse, il suffit d’interchanger les variables dépendante et indépendante.
La règle suivante représente le nombre de croissants |(n)| que l’on peut acheter avec |6\ $| en fonction du prix en |$| d’un croissant |(p).| ||n=\dfrac{6}{p}||Quelle est la règle de la réciproque, c’est-à-dire la règle qui donne le prix d’un croissant en fonction du nombre de croissants qu’on a réussi à acheter avec |6\ $|?
On obtient la règle de la réciproque en interchangeant simplement les variables |n| et |p.| ||\begin{align} \color{#3B87CD}n &= \dfrac{6}{\color{#FF55C3}p} \\ \color{#FF55C3}p &= \dfrac{6}{\color{#3B87CD}n} \end{align}||Réponse : La réciproque est |p=\dfrac{6}{n}.|
Remarque : Le graphique de la fonction de variation inverse et celui de sa réciproque sont identiques. On obtient chaque point de la réciproque en interchangeant les coordonnées des points de la fonction de départ.
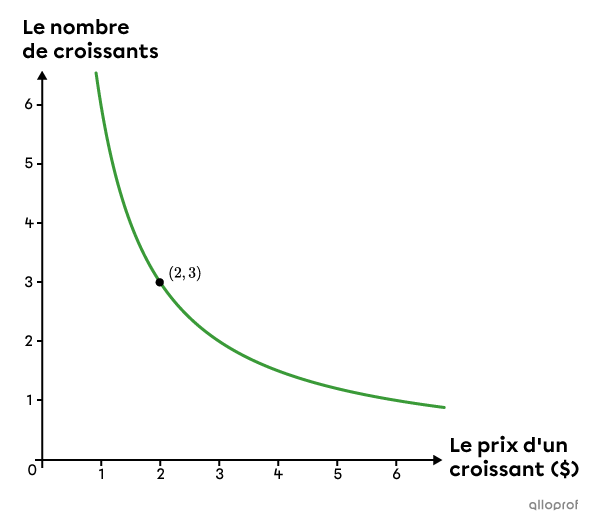
Le point |(2,3)| indique que si le prix d’un croissant est de |2\ $,| alors il est possible d’en acheter |3| avec un budget de |6\ $.|
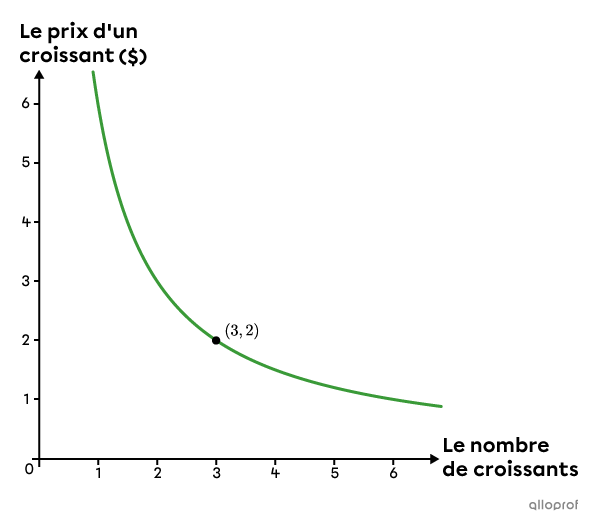
Le point |(3,2)| indique que si on a réussi à acheter 3 croissants avec notre budget de |6\ $,| c’est que chaque croissant se vendait à un prix unitaire de |2\ $.|
Pour valider ta compréhension à propos des situations de proportionnalité et des situations inversement proportionnelles de façon interactive, consulte la MiniRécup suivante :
