The Mayer line method is a procedure for generating a regression line for a given scatter plot by calculating means (averages). This line can be used to interpolate or extrapolate values, in other words, to make predictions.
The following steps are used to find the rule of the Mayer line and to make predictions from a 2-variable data set.
-
Order the coordinates according to the independent variable.
-
Separate the distribution into 2 equal groups, if possible.
-
Calculate the mean points of each group |(P_1| and |P_2).|
-
Find the rule of the regression line that passes through the points |(P_1| and |P_2).|
-
Predict values using the rule of the line.
Following a survey of |16| Quebec families, the total spending on sports and recreation was examined in relation to their household income.
The following table of values shows the data collected. The data was then placed on a Cartesian plane to create a scatter plot.
| Household income ($/year) |
|125\ 000| | |65\ 000| | |35\ 000| | |145\ 000| | |130\ 000| | |80\ 000| | |50\ 000| | |40\ 000| |
|---|---|---|---|---|---|---|---|---|
| Spending on sports and recreation ($/year) |
|10\ 000| | |8\ 000| | |1\ 000| | |9\ 000| | |8\ 000| | |6\ 000| | |4\ 000| | |2\ 000| |
| Household income ($/year) |
|90\ 000| | |20\ 000| | |75\ 000| | |105\ 000| | |100\ 000| | |140\ 000| | |150\ 000| | |65\ 000| |
| Spending on sports and recreation ($/year) |
|10\ 000| | |500| | |4\ 000| | |6\ 000| | |8\ 000| | |13\ 000| | |5\ 000| | |5\ 000| |
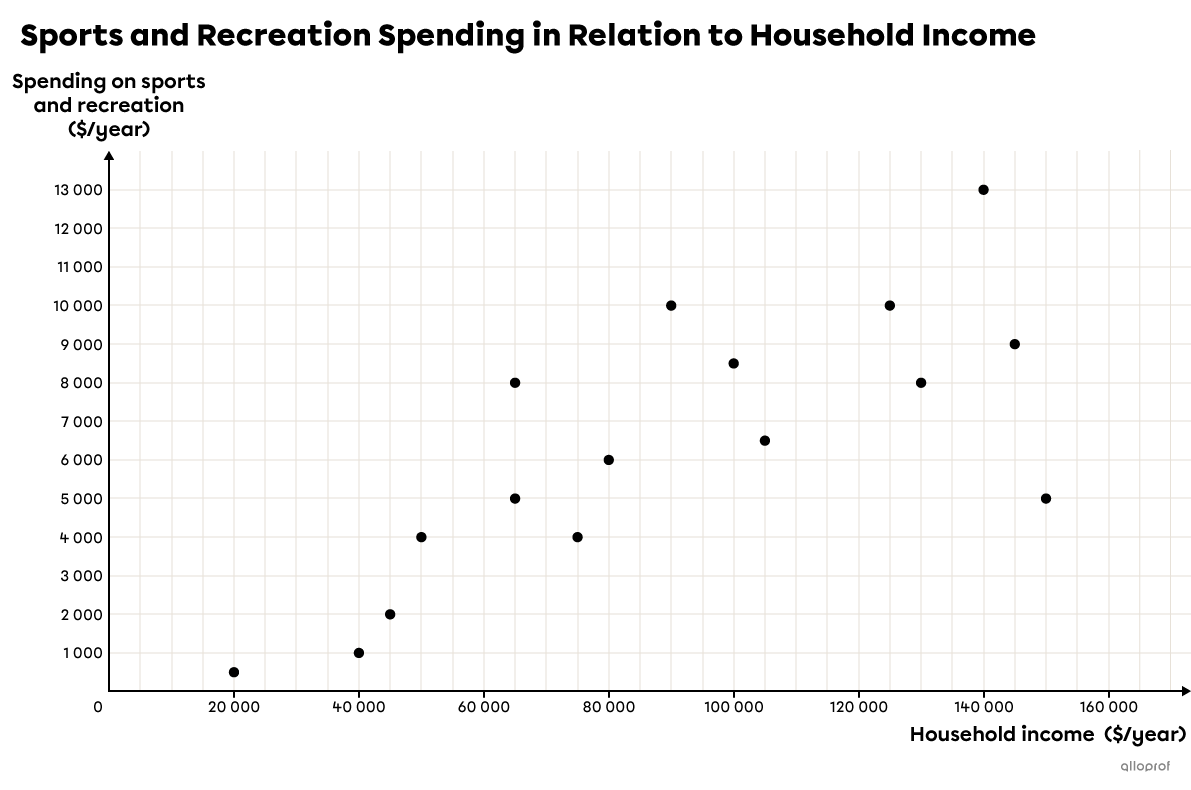
a) A family has an annual household income of |$250\ 000|. If this family follows the same trend as the other Quebec families surveyed, how much do they budget for sports and recreation?
b) A family spends an average of | \$7500| a year on sports and recreation. What is their annual household income if they are a typical Quebec family?
-
Order the coordinates according to the independent variable.
| Household income ($/year) |
|20\ 000| | |35\ 000| | |40\ 000| | |50\ 000| | |65\ 000| | |65\ 000| | |75\ 000| | |80\ 000| |
|---|---|---|---|---|---|---|---|---|
| Spending on sports and recreation ($/year) |
|500| | |1\ 000| | |2\ 000| | |4\ 000| | |5\ 000| | |8\ 000| | |4\ 000| | |6\ 000| |
| Household income ($/year) |
|90\ 000| | |100\ 000| | |105\ 000| | |125\ 000| | |130\ 000| | |140\ 000| | |145\ 000| | |150\ 000| |
| Spending on sports and recreation ($/year) |
|10\ 000| | |8\ 000| | |6\ 000| | |10\ 000| | |8\ 000| | |13\ 000| | |9\ 000| | |5\ 000| |
-
Separate the distribution into 2 equal groups, if possible.
The distribution contains |16| pairs of data. The |8| pairs whose household income ranges from |20\ 000\ \$/\text{year}| to |80\ 000\ \$/\text{year}| make up the 1st group. The other |8| pairs form the 2nd group.
-
Calculate the mean points of each group |(P_1| and |P_2).|
Find the mean of the |x| and |y| values of each group to make 2 points.
| Mean of the x-values |\boldsymbol{(\overline{x})}| | Mean of the y-values |\boldsymbol{(\overline{y})}| | Mean point | |
|---|---|---|---|
| 1st group | |\begin{align}\overline{x}_1 &= \dfrac{\left(\begin{gathered}20\ 000+35\ 000+40\ 000+50\ 000\\+\,65\ 000+65\ 000+75\ 000+80\ 000\end{gathered}\right)}{8} \\ &= \dfrac{430\ 000}{8} \\ &=53\ 750 \end{align}| | |\begin{align}\overline{y}_1 &= \dfrac{\left(\begin{gathered}500+1000+2000+4000\\+\,5000+8000+4000+6000\end{gathered}\right)}{8} \\ &= \dfrac{30\ 500}{8} \\ &=3812.5 \end{align}| | |P_1(53\ 750, 3812.5)| |
| 2nd group | |\begin{align}\overline{x}_2 &= \dfrac{\left(\begin{gathered}90\ 000+100\ 000+105\ 000+125\ 000\\+\,130\ 000+140\ 000+145\ 000+150\ 000\end{gathered}\right)}{8} \\ &= \dfrac{985\ 000}{8} \\ &=123\ 125 \end{align}| | |\begin{align}\overline{y}_2 &= \dfrac{\left(\begin{gathered}10\ 000+8000+6000+10\ 000\\+\,8000+13\ 000+9000+5000\end{gathered}\right)}{8} \\ &= \dfrac{69\ 000}{8} \\ &=8625 \end{align}| | |P_2(123\ 125, 8625)| |
-
Find the rule of the regression line that passes through the points |\boldsymbol{P_1}| and |\boldsymbol{P_2}.|
Since this is a straight line, the rule has the form |y=ax+b.| We start by calculating the slope |(a).|
||\begin{align}a&=\dfrac{\overline{y}_2-\overline{y}_1}{\overline{x}_2-\overline{x}_1}\\&=\dfrac{8\ 625-3\ 812.5}{123\ 125-53\ 750}\\&\approx 0.07\end{align}|| Next, we replace |a| by |0.07| and the |x| and |y| variables by the coordinates of one of the 2 points. Then, we isolate |b.| ||\begin{align} y &= ax+b \\ y &= 0.07x+b \\ 8\ 625 &= 0.07(123\ 125)+b \\ 8625 &\approx 8619+b \\ 6 &\approx b \end{align}||So, the rule of the Mayer line is |y=0.07x+6,| where |x| is the household income and |y| is the spending on sports and recreation, both in |\$| per year. We can graph this line.
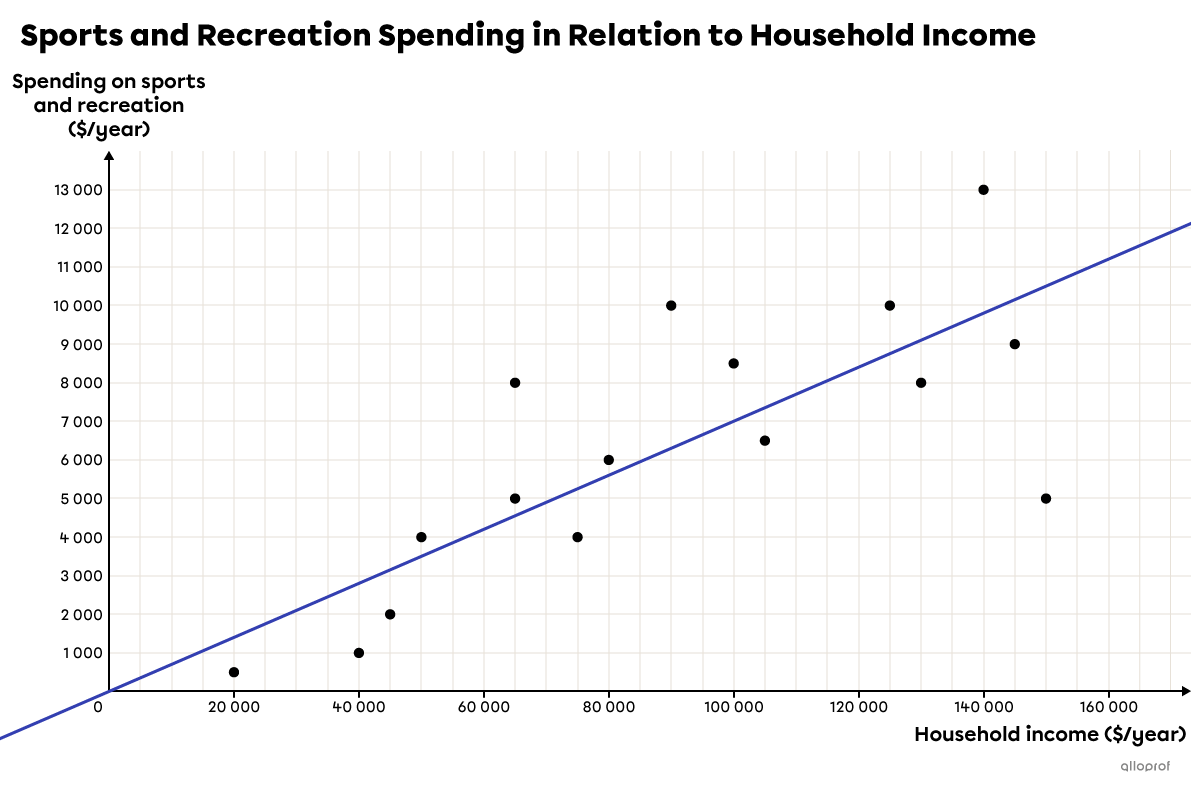
-
Predict values using the rule of the line.
a) A family has an annual household income of | \$250\ 000|. If this family follows the same trend as the other Quebec families surveyed, how much do they budget for sports and recreation?
We can estimate this family's spending on sports and recreation using the regression line. Since the household income in question | \$250\ 000| is outside the range studied (| \$20\ 000| to | \$150\ 000|), this is an extrapolation.
We replace the |x| variable with |250\ 000| in the regression line rule and complete the calculation. ||\begin{align}y&=0.07x+6\\y&=0.07(250\ 000)+6\\y&=17\ 500+6\\y&=\$17\ 506\ \end{align}||Answer: A household with an annual income of | \$250\ 000| would spend approximately | \$17\ 506| on sports and recreation if it followed the same trend as the other Quebec families surveyed.
b) A family spends an average of | \$7500| a year on sports and recreation. What is their annual household income if they are a typical Quebec family?
We can estimate the annual household income of this family using the regression line. This is an interpolation because the annual budget for recreation and sports |( \$7500)| is within the interval studied |(500| to | \$13\ 000).|
We replace |y| with |7500| and isolate |x.| ||\begin{align} y &= 0.07x+6 \\ 7500 &= 0.07x+6 \\ 7500\boldsymbol{\color{#ec0000}{-6}} &= 0.07x+6 \boldsymbol{\color{#ec0000}{-6}} \\ \dfrac{7494}{\boldsymbol{\color{#ec0000}{0.07}}} &= \dfrac{0.07x}{\boldsymbol{\color{#ec0000}{0.07}}} \\\$ 107\ 057\ &\approx x \end{align}||Answer: If a household spends on average | \$7500| per year on sports and recreation, we can predict that the household income is about | \$107\ 057|.
Note: The same problem was solved in the regression line and median-median line concept sheets. In each case, comparable results were obtained.
When the points need to be ordered
-
Points are ordered according to their x-coordinates. The x- and y-coordinates should not each be ordered separately, they must be kept as an ordered pair.
-
If 2 points have the same x-coordinate, but different y-coordinates, the one with the smaller y-coordinate is placed first.
Example:
Here is a table of values.
| |x| | |13| | |12| | |13| | |13| | |10| | |12| |
|---|---|---|---|---|---|---|
| |y| | |35| | |24| | |35| | |28| | |25| | |29| |
We get the following table.
| |x| | |10| | |12| | |12| | |13| | |13| | |13| |
|---|---|---|---|---|---|---|
| |y| | |25| | |24| | |29| | |28| | |35| | |35| |
We do not get this one.
| |x| | |10| | |12| | |12| | |13| | |13| | |13| |
|---|---|---|---|---|---|---|
| |y| | |24| | |25| | |28| | |29| | |35| | |35| |
When the points need to be separated into 2 groups
-
If the number of points can be divided evenly by 2, the groups are equal.
For example, 16 = 8 + 8. -
If the number of points cannot be divided evenly by 2, one can choose to ignore the middle pair or to include it in one of the 2 groups, as desired.
For example, 29 = 15 + 14 or 14 + 15 or 14 + 14 + a data value that is left out.
The Mayer line method is generally faster to perform than the median-median line method, but it is not always the best method. Here is an example where the two approaches are presented in parallel so that they can be compared.
During a hockey season, the points scored by all players are counted. A player's points include both their assists and the goals they scored. In hockey, up to 2 assists are counted for each goal scored, which corresponds to the last 2 passes made just before a goal.
Here are the numbers of assists and points for 10 regular Boston Bruins forwards during the 2022-2023 NHL season.
| Player | Number of assists | Number of points |
|---|---|---|
| D. Pastrnak | ||49|| | ||109|| |
| B. Marchand | ||46|| | ||66|| |
| P. Zacha | ||37|| | ||58|| |
| P. Bergeron | ||30|| | ||57|| |
| D. Krejci | ||40|| | ||56|| |
| J. DeBrusk | ||23|| | ||48|| |
| C. Coyle | ||29|| | ||44|| |
| T. Hall | ||20|| | ||36|| |
| T. Frederic | ||14|| | ||30|| |
| N. Foligno | ||16|| | ||28|| |
Based on this team's data, a player who made 60 assists should have finished the season with how many points?
-
Order the coordinates according to the independent variable.
| Number of assists | |14| | |16| | |20| | |23| | |29| | |30| | |37| | |40| | |46| | |49| |
|---|---|---|---|---|---|---|---|---|---|---|
| Number of points | |30| | |28| | |36| | |48| | |44| | |57| | |58| | |56| | |66| | |109| |
The Mayer line
-
Separate the distribution into 2 equal groups, if possible.
The 1st group is formed by the |5| pairs with a number of assists of |29| or less. The other |5| pairs form the 2nd group.
-
Calculate the mean points of each group |\boldsymbol{(P_1}| and |\boldsymbol{P_2)}|
| Mean of the x-values |\boldsymbol{(\overline{x})}| | Mean of the y-values |\boldsymbol{(\overline{y})}| | Mean point | |
| 1st group | |\begin{align}\overline{x}_1 &= \dfrac{14+16+20+23+29}{5} \\ &=20.4\end{align}| | |\begin{align}\overline{y}_1 &= \dfrac{30+28+36+48+44}{5} \\ &=37.2\end{align}| | |P_1(20.4, 37.2)| |
| 2nd group | |\begin{align}\overline{x}_2 &= \dfrac{30+37+40+46+49}{5} \\ &=40.4\end{align}| | |\begin{align}\overline{y}_2 &= \dfrac{57+58+56+66+109}{5} \\ &=69.2\end{align}| | |P_2(40.4,69.2)| |
-
Find the rule of the regression line that passes through the points |\boldsymbol{P_1}| and |\boldsymbol{P_2}.|
Since this is a straight line, the rule has the form |y=ax+b.| We start by calculating the slope |(a).| ||\begin{align}a&=\dfrac{\overline{y}_2-\overline{y}_1}{\overline{x}_2-\overline{x}_1}\\&=\dfrac{69.2-37.2}{40.4-20.4}\\&= 1.6\end{align}||Next, we replace |a| by |1.6| and the |x| and |y| variables by the coordinates of one of the 2 points. Then, we isolate |b.| ||\begin{align} y &= ax+b \\ y &= 1.6x+b \\ 37.2 &= 1.6(20.4)+b \\ 37.2 &= 32.64+b \\ 4.56 &= b \end{align}||So, the rule for the regression line found using the Mayer line method is |\color{#3b87cd}{y=1.6x+4.56},| where |x| is the number of assists and |y,| the number of points.
-
Predict values using the rule of the line.
This is an extrapolation, since the number of assists |(60)| is outside the interval studied |(14| to |49).| The number of points can now be estimated using the Mayer line by replacing |x| with |60.| ||\begin{align} y &= 1.6x+4.56 \\&= 1.6(60)+4.56 \\ &= 96+4.56\\&= 100.56\\ &\approx 101\ \text{points} \end{align}||
The Median-Median line
-
Separate the distribution into 3 equal groups, if possible.
The 1st and 3rd groups have |3| data pairs each and the 2nd has |4.|
-
Calculate the median points of each group |\boldsymbol{(M_1, M_2}| and |\boldsymbol{M_3)}|
| Median of the x-values|\boldsymbol{(x)}| | Median of the y-values |\boldsymbol{(y)}| | Mean point | |
| 1st group | |x_1=16| | |y_1=30| | |M_1(16,30)| |
| 2nd group | |\begin{align}x_2&=\dfrac{29+30}{2}\\&=29.5\end{align}| | |\begin{align}y_2&=\dfrac{48+57}{2}\\&=52.5\end{align}| | |M_2(29.5,52.5)| |
| 3rd group | |x_3=46| | |y_3=66| | |M_3(46,66)| |
-
Calculate the mean point |\boldsymbol{P},| whose coordinates are the mean of the x-coordinates and the mean of the y-coordinates of the points |\boldsymbol{M_1, M_2}| and |\boldsymbol{M_3}|
||P\left(\dfrac{16+29.5+46}{3},\dfrac{30+52.5+66}{3}\right)=(30.5,49.5)||
-
Find the rate of change |\boldsymbol{(a)}| of the line that passes through |\boldsymbol{M_1}| and |\boldsymbol{M_3}| ||\begin{align}a&=\dfrac{y_3-y_1}{x_3-x_1}\\&=\dfrac{66-30}{46-16}\\&=1.2\end{align}||
-
Find the y-intercept |\boldsymbol{(b)}| of the line that passes through |\boldsymbol{P}| and for which the rate of change is |\boldsymbol{a}| ||\begin{align} y &= ax+b \\ y &= 1.2x+b \\ 49.5 &= 1.2(30.5)+b \\ 49.5 &= 36.6+b \\ 12.9 &= b \end{align}||So, the rule of the median-median line is |\color{#560fa5}{y=1.2x+12.9},| where |x| is the number of assists and |y,| the number of points.
-
Predict values using the rule of the line.
The number of points is extrapolated using the median-median line by replacing the |x| variable with |60.| ||\begin{align} y &= 1.2x+12.9 \\&= 1.2(60)+12.9 \\ &= 72+12.9 \\ &= 84.9\\ &\approx 85\ \text{points} \end{align}||
Answer: A player who makes |60| assists in a season should get about |85| points according to the median-median line or |101| points according to the Mayer line.
The Mayer method is based on the calculation of the mean. However, the mean is a measure of central tendency that is very much influenced by distant data, known as outliers. In contrast, the median-median method is not influenced by outliers.
In other words, when there are one or more outliers in a distribution, the predictions made using the Mayer line are less reliable, or less representative of the whole data set, than those made using the median-median line. The latter method should therefore be used in these situations.
Let's go back to the example of the Boston Bruins players' points to see which answer is more reliable between the answer obtained using the Mayer line and the answer obtained using the median-median line.
Let's start by plotting the scatterplot and the 2 lines on the same graph.
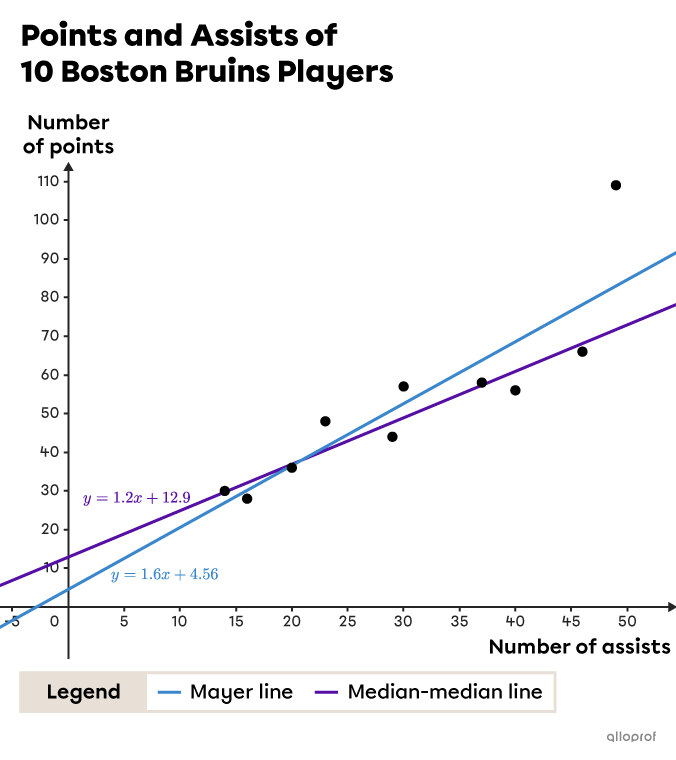
First of all, we notice that the slope of the two lines is quite different. The rate of change for the median-median line is |1.2,| whereas the slope of the Mayer line is |1.6.|
We also notice that the point |(49,109),| which represents David Pastrnak's data, is far from the others. This player accumulated far more total points in relation to his number of assists than the rest of his team |\left(\dfrac{109}{49} \approx 2.22\right).|
Pastrnak's data had an impact on the Mayer method, since it was included in the calculation of the mean points. This had the effect of increasing the value of the slope of the Mayer line compared to the other method. The point |(49,109),| even if it is high, it does not influence the median points. This is why the median-median line is less steep and fits the data set better, as seen on the graph. On the contrary, the Mayer line is more inclined towards the point |(49,109)| and therefore less fitted to the rest of the scatter plot.
Conclusion: Therefore, predictions made using the median-median line are considered to be more representative of all players. So, a player who makes |60| assists in a season should earn about |85| points and not |101.|