The triangular ruler, also known as the scale ruler, architect’s ruler or kutsch, is a tool that allows you to draw lines and take measurements at a specific scale without having to do any calculations.
By knowing the scale of a drawing, the graduations of the triangular ruler can be used to determine the actual dimensions of the object drawn.
Depending on the model, the triangular ruler offers many different scales such as 1:1, 1:5, 1:8, 1:10, 1:20, 1:25, 1:75, 1:50, 1:100, 1:250, etc.
In addition, different units of measurement are used on different sides. Generally these are millimetres (mm), centimetres (cm) or metres (m).
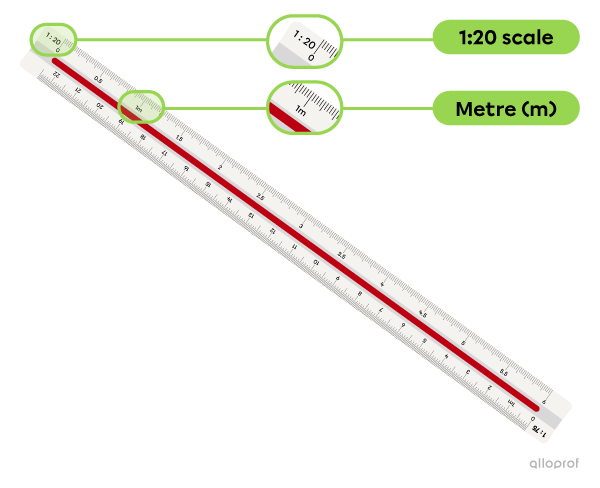
This side of the ruler includes a 1:20 reduction scale and the unit of measurement is the metre (m).
Here’s how to make a scale drawing with a triangular ruler.
-
Determine the scale to be used for the drawing.
-
Locate the edge of the triangular ruler that corresponds to the chosen scale.
-
Align the 0 on the triangular ruler with the start of the line to be traced and mark it.
-
Measure and mark the actual measurement.
-
Draw the line using the appropriate technical drawing instruments.
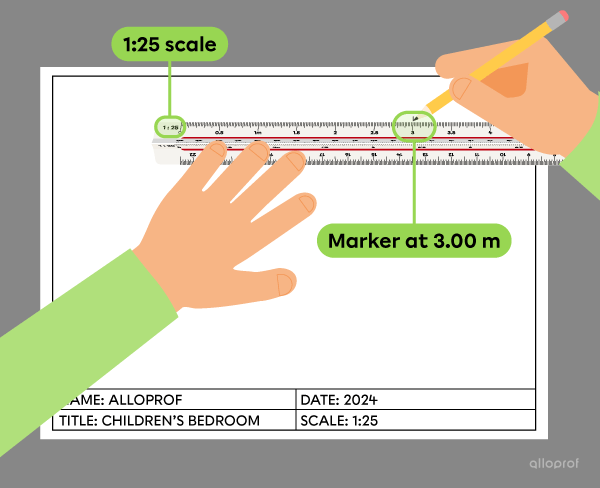
To design a children’s bedroom, start with drawing a 3.00-m square on a 1:25 scale.
-
According to the situation, the scale to be used is 1:25.
-
Look for the edge of the ruler marked with the 1:25 scale.
-
Align the 0 with the start of the line to be made and make a mark.
-
Another mark is made at the actual length of one side of the square, i.e. 3.00 m.
-
Draw the first straight line from the mark 0 to the mark at 3.00 m. This is the first side of the square.

Repeat the same steps to draw the other sides of the square.
The resulting square on the plan represents the actual size of the bedroom walls at a reduction scale of 1:25.

If you know the scale at which a drawing was made, you can use the triangular ruler to measure any line or distance and obtain its actual size. Here’s how to do it.
-
Identify the scale of the drawing. This information is usually noted in the title block.
-
Choose the edge of the triangular ruler that corresponds to the scale of the drawing.
-
Align the 0 on the triangular ruler with the start of the measurement to be taken.
-
Read the measurement. This corresponds to the actual measurement.
We want to determine the actual distance between two beds on the floor plan of a children’s bedroom. Here are the steps to follow.
-
In the title block you can see that the scale of the plan is 1:25.
-
We choose the edge of the ruler with the scale 1:25 to measure the distance between the two beds.
-
Align the 0 on the ruler with the edge of the first bed.
-
We measure the distance to the edge of the second bed and obtain 1.12 m.
The actual distance between the two beds is 1.12 m.
