Généralement, la vitesse de réaction a tendance à changer au cours d’une réaction chimique. Le graphique suivant représente ce qu’on observe généralement au cours d’une réaction d’ordre 1 ou d’ordre 2.
-
Au début d’une réaction, la concentration des réactifs est élevée, cela signifie que plusieurs particules de réactifs peuvent subir des collisions efficaces. Cela entraine une vitesse de réaction initiale élevée.
-
Au fur et à mesure que les réactifs sont transformés en produits, leur concentration diminue et il y a moins de particules de réactifs qui peuvent subir des collisions efficaces. Cela entraine une vitesse de réaction plus faible.
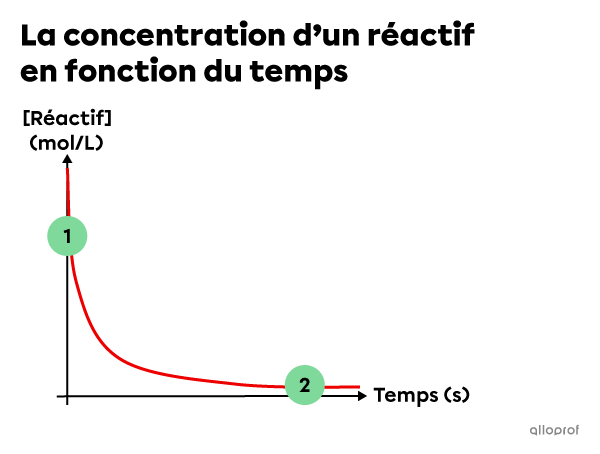
Compte tenu de cette progression, il peut être pertinent de calculer la vitesse de réaction à un moment spécifique ou pour l’ensemble de la réaction.
Considérons l’analogie suivante : lorsqu’un camion transporte des marchandises entre deux villes, sa vitesse varie. La vitesse du camion est élevée sur l’autoroute et diminue considérablement en ville. Il est possible de déterminer la vitesse du camion à chaque instant. Il est aussi possible de déterminer la vitesse moyenne du camion pour l’ensemble du trajet ou pour une période donnée. De même, il est possible de déterminer la vitesse de réaction moyenne et la vitesse de réaction instantanée d’une réaction chimique.
-
La vitesse de réaction moyenne est la variation de la quantité d’un réactif ou d’un produit donné au cours d’une période de temps déterminée.
-
La vitesse de réaction instantanée est la vitesse à un instant précis au cours d’une réaction chimique.
La vitesse de réaction moyenne correspond à la pente de la sécante tracée entre deux points quelconques d’une courbe d’un graphique de la concentration en fonction du temps.
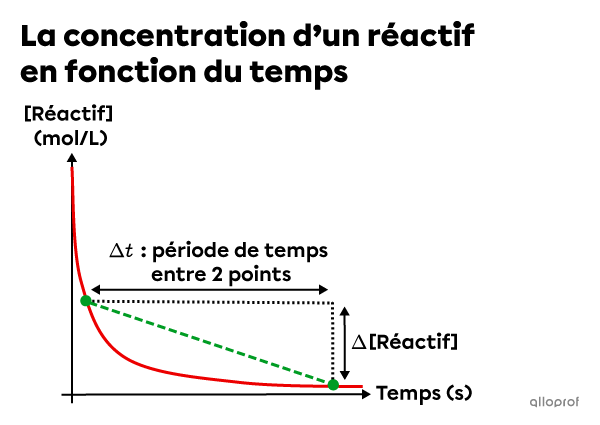
La vitesse de réaction moyenne peut être calculée à l’aide de la formule suivante.
||v_{moyenne}=\vert \text{pente}_{\text{sécante}}\vert=\dfrac{\vert \Delta [\text{Réactif}]\vert}{\Delta t}||
La vitesse de réaction instantanée correspond à la pente de la tangente qui touche la courbe d’un graphique de la concentration en fonction du temps à un moment précis.
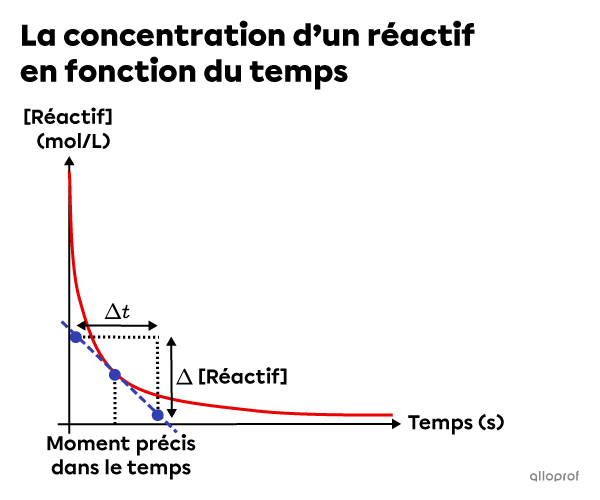
La vitesse de réaction instantanée peut être calculée à l’aide de la formule suivante.
||v_{instantanée}=\vert \text{pente}_{\text{tangente}}\vert=\dfrac{\vert \Delta [\text{Réactif}]\vert}{\Delta t}||
Il existe plusieurs méthodes pour déterminer la vitesse d’une réaction. La méthode est généralement choisie en fonction de ce qu’on souhaite déterminer, soit la vitesse de réaction moyenne, soit la vitesse de réaction instantanée.
Au cours d’une réaction, les données récoltées selon des intervalles réguliers sont généralement présentées dans un tableau et dans un graphique. Ces informations peuvent être utilisées pour déterminer la vitesse de réaction moyenne.
La vitesse de réaction moyenne peut être calculée entre deux points quelconques de la courbe de la variation de la quantité d’un produit ou d’un réactif en fonction du temps.
La vitesse de réaction moyenne correspond à la valeur absolue de la pente de la sécante qui coupe la courbe en deux points quelconques.
Du magnésium |(\text{Mg})| et de l’acide sulfurique |(\text{H}_2\text{SO}_4)| réagissent pour former du sulfate de magnésium |(\text{Mg}\text{SO}_4)| et du dihydrogène |(\text{H}_2)| selon l’équation chimique suivante.
||\text{Mg}_{\text{(s)}} + \text{H}_2\text{SO}_{4\text{(aq)}} \rightarrow \text{MgSO}_{4\text{(aq)}} + \text{H}_{2\text{(g)}}||
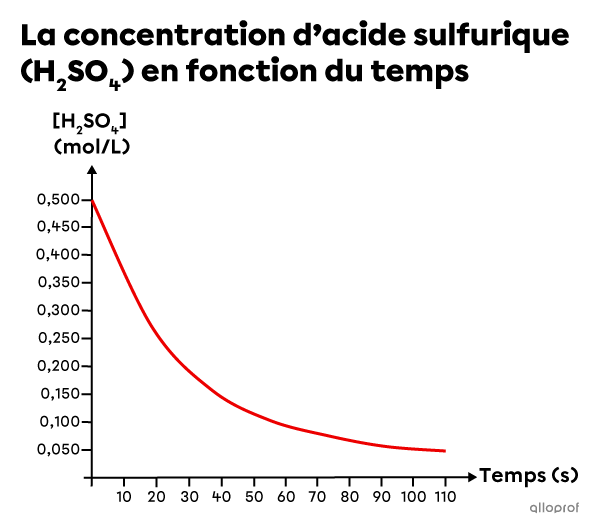
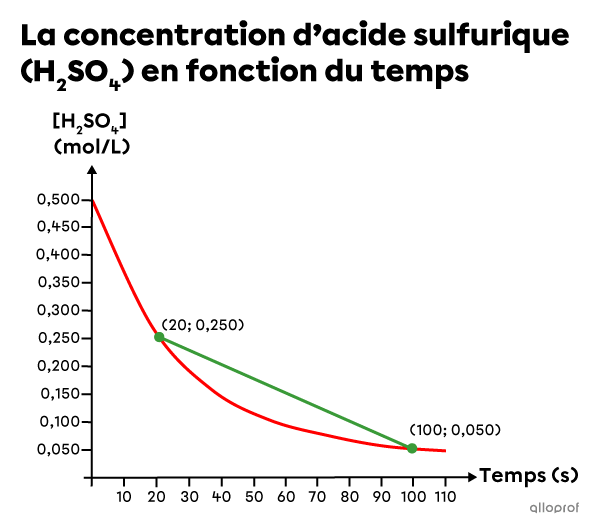
En se basant sur les données expérimentales, un graphique est créé pour montrer la diminution de la concentration de |\text{H}_2\text{SO}_{4}| en fonction du temps.
Détermine la vitesse de réaction moyenne entre |20\ \text{s}| et |100\ \text{s}.|
-
On dessine une sécante qui coupe la courbe à |20\ \text{s}| et à |100\ \text{s},| puis on identifie la valeur de la concentration à ces deux moments.
|\begin{align}
t_1&= 20\ \text{s}\\
[\text{H}_2\text{SO}_4]_1&= 0{,}250\ \text{mol/L}\\
t_2&= 100\ \text{s}\\
[\text{H}_2\text{SO}_4]_2&= 0{,}050\ \text{mol/L}
\end{align}|
-
On utilise ces valeurs pour déterminer la vitesse de réaction moyenne. Celle-ci correspond à la valeur absolue de la pente de la sécante.
|\begin{align}
v_{moyenne}&=\vert \text{pente}_{\text{sécante}}\vert=\dfrac{\vert \Delta [\text{H}_2\text{SO}_4]\vert}{\Delta t}\\\\
v_{moyenne}&=\dfrac{\vert [\text{H}_2\text{SO}_4]_2 - [\text{H}_2\text{SO}_4]_1\vert}{t_2 - t_1}\\\\
v_{moyenne}&= \dfrac{\vert 0{,}050\ \text{mol/L} - 0{,}250\ \text{mol/L}\vert}{100\ \text{s} - 20\ \text{s}}\\\\
v_{moyenne}&= 2{,}5\times10^{-3}\ \text{mol/L}\cdot\text{s}
\end{align}|
Du magnésium |(\text{Mg})| et de l’acide chlorhydrique |(\text{HCl})| réagissent pour former du dichlorure de magnésium |(\text{MgCl}_2)| et du dihydrogène |(\text{H}_2)| selon l’équation suivante.
||\text{Mg}_{\text{(s)}}+2\ \text{HCl}_\text{(aq)}\rightarrow\text{MgCl}_{2\text{(aq)}}+\text{H}_{2\text{(g)}}||
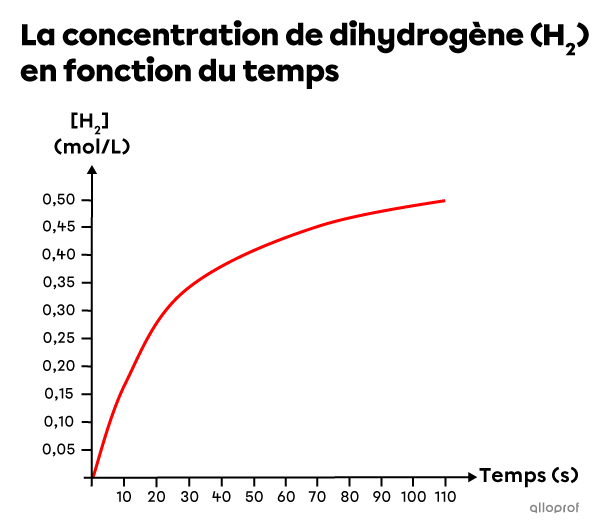
En se basant sur les données expérimentales, un graphique est créé pour montrer l’augmentation de la concentration de |\text{H}_2| en fonction du temps.
Détermine la vitesse de réaction moyenne entre le début de la réaction et |70\ \text{s}.|
-
On dessine une sécante qui coupe la courbe à |0\ \text{s}| et à |70\ \text{s},| puis on identifie la valeur de la concentration à ces deux moments.
|\begin{align}
t_1&= 0\ \text{s}\\
[\text{H}_2]_1&= 0{,}00\ \text{mol/L}\\
t_2&= 70\ \text{s}\\
[\text{H}_2]_2&= 0{,}45\ \text{mol/L}
\end{align}|
-
On utilise ces valeurs pour déterminer la vitesse de réaction moyenne. Celle-ci correspond à la valeur absolue de la pente de la sécante.
|\begin{align}
v_{moyenne}&=\vert \text{pente}_{\text{sécante}}\vert=\dfrac{\vert \Delta [\text{H}_2]\vert}{\Delta t}\\\\
v_{moyenne}&=\dfrac{\vert [\text{H}_2]_2 - [\text{H}_2]_1\vert}{t_2 - t_1}\\\\
v_{moyenne}&= \dfrac{\vert 0{,}45\ \text{mol/L} - 0{,}00\ \text{mol/L}\vert}{70\ \text{s} - 0\ \text{s}}\\\\
v_{moyenne}&\approx 6{,}4\times10^{-3}\ \text{mol/L}\cdot\text{s}
\end{align}|

La vitesse de réaction instantanée peut être calculée à partir d’un graphique de la variation de la quantité d’un réactif ou d’un produit en fonction du temps. La vitesse d’une réaction à un moment donné correspond à la valeur absolue de la pente de la tangente qui touche la courbe à ce moment.
Du dihydrogène |(\text{H}_2)| et du diiode |(\text{I}_2)| réagissent pour former de l’iodure d’hydrogène |(\text{HI})| selon l’équation chimique suivante.
||{\text{H}_{2{\text{(g)}}} + \text{I}_{2{\text{(g)}}} \rightarrow 2\ \text{HI}_{\text{(g)}}}||
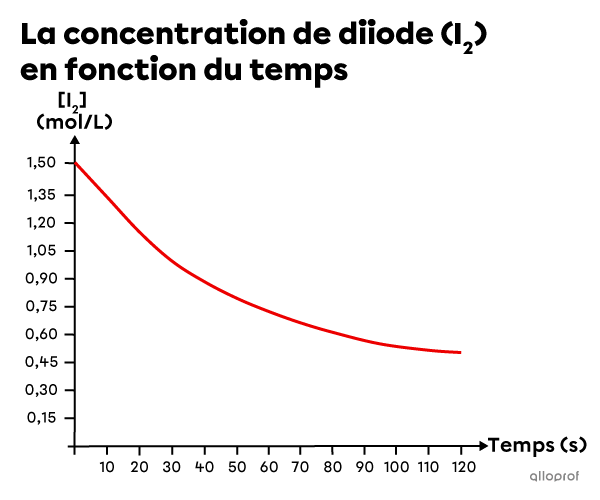
En se basant sur les données expérimentales, un graphique est créé pour montrer la diminution de la concentration de |\text{I}_2| en fonction du temps.
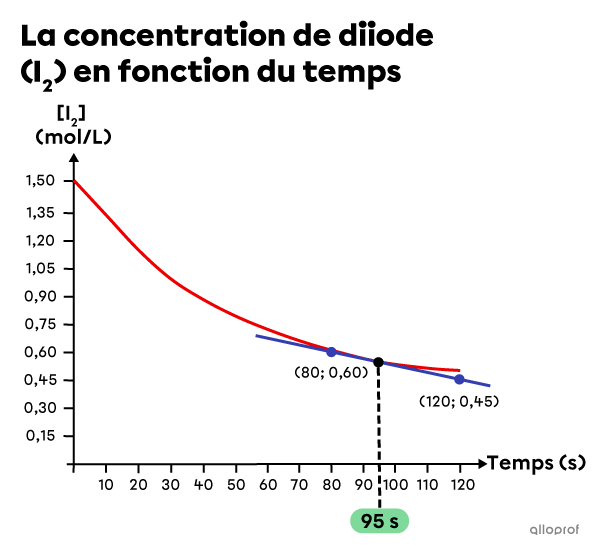
Détermine la vitesse de réaction instantanée à |95\ \text{s}.|
-
On dessine une tangente qui touche la courbe au moment qui nous intéresse, soit |95\ \text{s},| puis on choisit deux points de la tangente et on identifie leurs coordonnées.
|\begin{align}
t_1&= 80\ \text{s}\\
[\text{I}_2]_1&= 0{,}60\ \text{mol/L}\\
t_2&= 120\ \text{s}\\
[\text{I}_2]_2&= 0{,}45\ \text{mol/L}
\end{align}|
-
On utilise ces valeurs pour déterminer la vitesse de réaction instantanée. Celle-ci correspond à la valeur absolue de la pente de la tangente.
|\begin{align}
v_{instantanée}&=\vert \text{pente}_{\text{tangente}}\vert=\dfrac{\vert \Delta [\text{I}_2]\vert}{\Delta t}\\\\
v_{instantanée}&=\dfrac{\vert [\text{I}_2]_2 - [\text{I}_2]_1\vert}{t_2 - t_1}\\\\
v_{instantanée}&= \dfrac{\vert 0{,}45\ \text{mol/L} - 0{,}60\ \text{mol/L}\vert}{120\ \text{s} - 80\ \text{s}}\\\\
v_{instantanée}&\approx 3{,}8\times10^{-3}\ \text{mol/L}\cdot\text{s}
\end{align}|
Du dioxyde d’azote |(\text{NO}_2)| et du monoxyde de carbone |(\text{CO})| réagissent pour former du monoxyde d’azote |(\text{NO})| et du dioxyde de carbone |(\text{CO}_2)| selon l’équation suivante.
||\text{NO}_{2\text{(g)}} + \text{CO}_{\text{(g)}} \rightarrow \text{NO}_{\text{(g)}} + \text{CO}_{2\text{(g)}}||
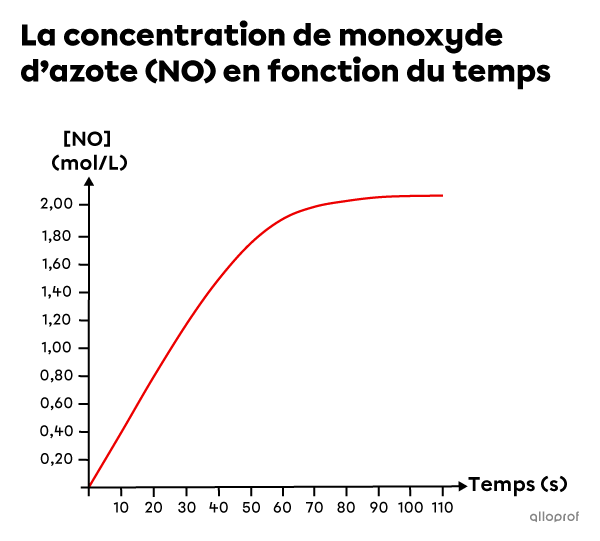
En se basant sur les données expérimentales, un graphique est créé pour montrer l’augmentation de la concentration de |\text{NO}| en fonction du temps.
Détermine la vitesse de réaction instantanée à |60\ \text{s}.|
-
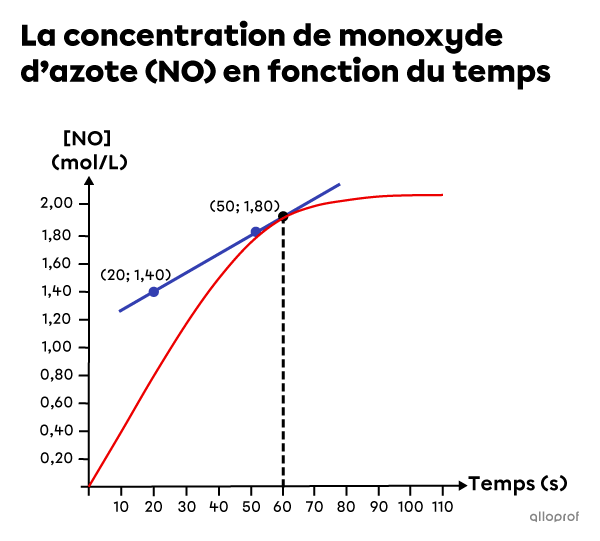
On dessine une tangente qui touche la courbe au moment qui nous intéresse, soit |60\ \text{s},| puis on choisit deux points de la tangente et on identifie leurs coordonnées.
|\begin{align}
t_1&= 20\ \text{s}\\
[\text{NO}]_1&= 1{,}40\ \text{mol/L}\\
t_2&= 50\ \text{s}\\
[\text{NO}]_2&= 1{,}80\ \text{mol/L}
\end{align}|
-
On utilise ces valeurs pour déterminer la vitesse de réaction instantanée. Celle-ci correspond à la valeur absolue de la pente de la tangente.
|\begin{align}
v_{instantanée}&=\vert \text{pente}_{\text{tangente}}\vert=\dfrac{\vert \Delta[\text{NO}]\vert}{\Delta t}\\\\
v_{instantanée}&=\dfrac{\vert [\text{NO}]_2 - [\text{NO}]_1\vert}{t_2 - t_1}\\\\
v_{instantanée}&= \dfrac{\vert 1{,}80\ \text{mol/L} - 1{,}40\ \text{mol/L}\vert}{50\ \text{s} - 20\ \text{s}}\\\\
v_{instantanée}&\approx 1{,}3\times10^{-2}\ \text{mol/L}\cdot\text{s}
\end{align}|
Pour déterminer la vitesse moyenne ou instantanée d’une réaction, il est généralement nécessaire de tracer un graphique en utilisant les données expérimentales.
Du calcium |(\text{Ca})| et de l’acide chlorhydrique |(\text{HCl})| réagissent pour former du dichlorure de calcium |(\text{CaCl}_2)| et du dihydrogène |(\text{H}_2)| selon l’équation chimique suivante.
||\text{Ca}_{\text{(s)}} + 2\ \text{HCl}_{\text{(aq)}}\rightarrow \text{CaCl}_{2\text{(aq)}} + \text{H}_{2\text{(g)}}||
Le tableau suivant présente les données recueillies durant l’expérience. Il s’agit du volume de dihydrogène |(\text{H}_2)| en fonction du temps.
|
Temps |\text{(s)}| |
|0| |
|15| |
|30| |
|45| |
|60| |
|75| |
|90| |
|105| |
|120| |
|135| |
|150| |
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|V_{\text{H}_2}\ \text{(mL)}| |
|0{,}00| |
|10{,}00| |
|19{,}00| |
|28{,}00| |
|36{,}00| |
|41{,}00| |
|44{,}00| |
|46{,}50| |
|48{,}00| |
|49{,}50| |
|50{,}00| |
a) Détermine la vitesse de réaction moyenne au cours des premières |55\ \text{s}.|
b) Estime la vitesse de réaction instantanée à |70\ \text{s}.|
Du calcium |(\text{Ca})| et de l’acide chlorhydrique |(\text{HCl})| réagissent pour former du dichlorure de calcium |(\text{CaCl}_2)| et du dihydrogène |(\text{H}_2)| selon l’équation chimique suivante.
||\text{Ca}_{\text{(s)}} + 2\ \text{HCl}_{\text{(aq)}}\rightarrow \text{CaCl}_{2\text{(aq)}} + \text{H}_{2\text{(g)}}||
Le tableau suivant présente les données recueillies durant l’expérience. Il s’agit du volume de dihydrogène |(\text{H}_2)| en fonction du temps.
|
Temps |\text{(s)}| |
|0| |
|15| |
|30| |
|45| |
|60| |
|75| |
|90| |
|105| |
|120| |
|135| |
|150| |
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|V_{\text{H}_2}\ \text{(mL)}| |
|0{,}00| |
|10{,}00| |
|19{,}00| |
|28{,}00| |
|36{,}00| |
|41{,}00| |
|44{,}00| |
|46{,}50| |
|48{,}00| |
|49{,}50| |
|50{,}00| |
a) Détermine la vitesse de réaction moyenne au cours des premières |55\ \text{s}.|
b) Estime la vitesse de réaction instantanée à |70\ \text{s}.|
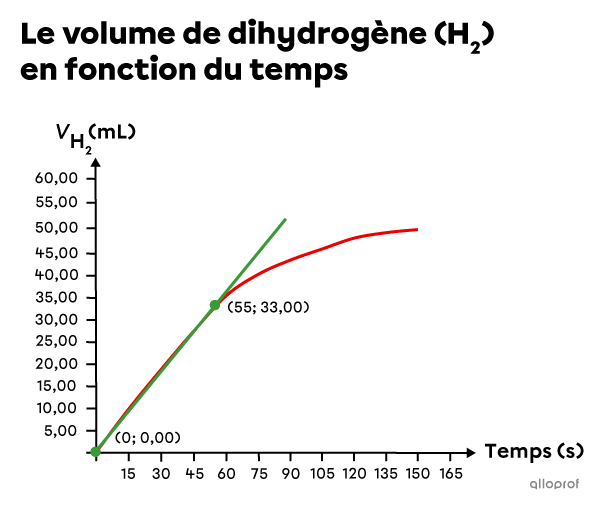
Il faut commencer par tracer le graphique du volume de dihydrogène |(\text{H}_2)| en fonction du temps.
a) Déterminer la vitesse de réaction moyenne au cours des premières |55\ \text{s}|
-
On dessine une sécante qui coupe la courbe à |0\ \text{s}| et à |55\ \text{s},| puis on identifie la valeur de la concentration à ces deux moments.
|\begin{align}
t_1&= 0\ \text{s}\\
V_{{\text{H}_{2_1}}}&= 0{,}00\ \text{mL}\\
t_2&= 55\ \text{s}\\
V_{{\text{H}_{2_2}}}&= 33{,}00\ \text{mL}
\end{align}|
-
On utilise ces valeurs pour déterminer la vitesse de réaction moyenne. Celle-ci correspond à la valeur absolue de la pente de la sécante.
|\begin{align}
v_{moyenne}&=\vert \text{pente}_{\text{sécante}}\vert=\dfrac{\vert \Delta V_{\text{H}_2}\vert}{\Delta t}\\\\
v_{moyenne}&=\dfrac{\vert V_{{\text{H}_{2_2}}} - V_{{\text{H}_{2_1}}}\vert}{t_2 - t_1}\\\\
v_{moyenne}&= \dfrac{\vert 33{,}00\ \text{mL} - 0{,}00\ \text{mL}\vert}{55\ \text{s} - 0\ \text{s}}\\\\
v_{moyenne}&= 0,60\ \text{mL/s}
\end{align}|
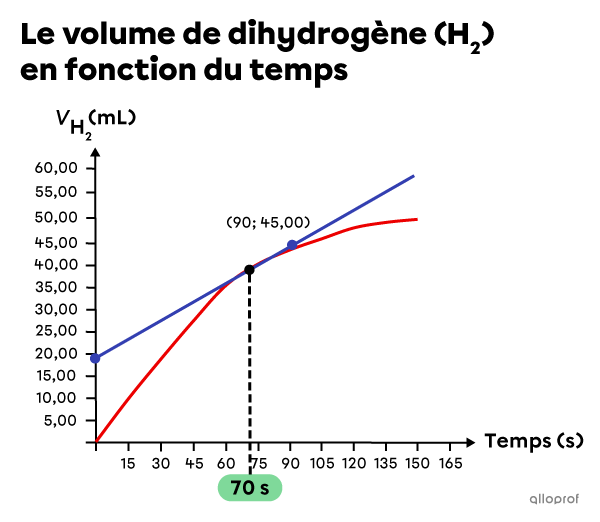
b) Estimer la vitesse de réaction instantanée à |70\ \text{s}|
-
On dessine une tangente qui touche la courbe au moment qui nous intéresse, soit |70\ \text{s},| puis on choisit deux points de la tangente et on identifie leurs coordonnées.
|\begin{align}
t_1&= 0\ \text{s}\\
V_{{\text{H}_{2_1}}}&= 20{,}00\ \text{mL}\\
t_2&= 90\ \text{s}\\
V_{{\text{H}_{2_2}}}&= 45{,}00\ \text{mL}
\end{align}|
-
On utilise ces valeurs pour déterminer la vitesse de réaction instantanée. Celle-ci correspond à la valeur absolue de la pente de la tangente.
|\begin{align}
v_{instantanée}&=\vert \text{pente}_{\text{tangente}}\vert=\dfrac{\vert \Delta V_{\text{H}_2}\vert}{\Delta t}\\\\
v_{instantanée}&=\dfrac{\vert V_{{\text{H}_{2_2}}} - V_{{\text{H}_{2_1}}}\vert}{t_2 - t_1}\\\\
v_{instantanée}&= \dfrac{\vert 45{,}00\ \text{mL} - 20{,}00\ \text{mL}\vert}{90\ \text{s} - 0\ \text{s}}\\\\
v_{instantanée}&\approx 0{,}28\ \text{mL/s}
\end{align}|
Parfois, la vitesse de réaction doit être déterminée en |\text{mol/s}| ou en |\text{mol/L}\cdot\text{s},| mais les données recueillies ne sont pas nécessairement en nombre de moles |\text{(mol)}|.
Les données telles que la masse |(m)| ou le volume |(V)| peuvent être converties en nombre de moles |(n)| à l’aide de la masse molaire |(M)|, de la loi d’Avogadro et du volume molaire ou de la loi des gaz parfaits.