Les fractions équivalentes | Primaire

Une fraction est équivalente à une autre lorsqu’elle représente la même partie d’un tout.

Pour bien comprendre ce qu’est une fraction équivalente, il faut avant tout connaitre le rôle du numérateur et du dénominateur dans une fraction. Pour savoir ce qu’est un numérateur et un dénominateur, tu peux lire la fiche La représentation d'une fraction.

Il faut bien s’assurer que les touts sont identiques, c’est-à-dire de la même grosseur, comme c'est le cas dans l'image suivante.

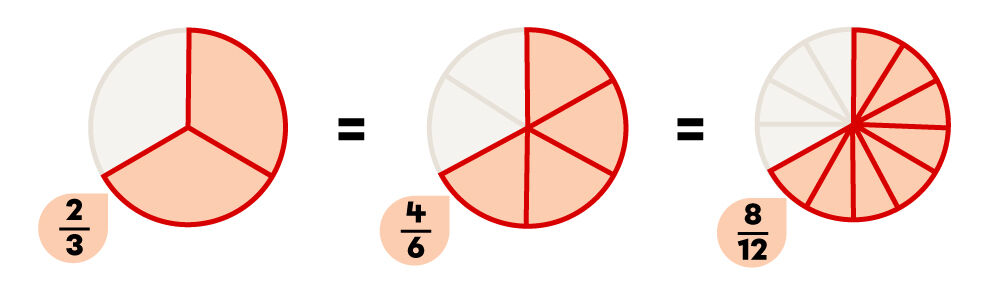
Sur cette image, tu peux aussi voir qu'utiliser |2| parties sur |3,| c’est équivalent à utiliser |4| parties sur |6| ou |8| parties sur |12.| La quantité utilisée représente donc la même partie du tout.

Pour vérifier si des fractions sont équivalentes, je dois suivre les étapes suivantes :

1. Je représente la fraction de mon choix.

2. Je représente la seconde fraction en utilisant le même tout. 

3. Je compare les deux fractions en observant les quantités utilisées.

Alicia a cuisiné |12| petits gâteaux. Le |\dfrac{1}{3}| de ses gâteaux ont un glaçage rouge et les |\dfrac{3}{12}| ont un glaçage bleu. Les gâteaux restants sont blancs.

Est-ce que la quantité de gâteaux rouges est équivalente à la quantité de gâteaux bleus?

Je représente la fraction de mon choix.  Je choisis d'abord de représenter la fraction |\dfrac{3}{12}.| Je sais que la quantité totale de gâteaux est |12| et que la quantité utilisée est |\dfrac{3}{12}.|
Je représente la seconde fraction en utilisant le même tout.  Je sais que la quantité totale de gâteaux est |12| et que la quantité utilisée est |\dfrac{1}{3}.| Je dois donc diviser la quantité totale en trois groupes égaux pour ensuite sélectionner un de ces |3| groupes.
Je compare les deux fractions en observant les quantités utilisées. La première fraction indique qu’elle a fait |3| gâteaux bleus et la seconde fraction, |4| gâteaux rouges.

La quantité de gâteaux rouges n’est pas équivalente à la quantité de gâteaux bleus, car Alicia a décoré |4| gâteaux en rouge et |3| gâteaux en bleu.

|\dfrac{3}{12}| n'est donc pas équivalent à |\dfrac{1}{3}.|

Une fraction est équivalente à une autre lorsqu’elle représente la même partie d’un tout.

Pour bien comprendre ce qu’est une fraction équivalente, il faut avant tout connaitre le rôle du numérateur et du dénominateur dans une fraction. Pour savoir ce qu’est un numérateur et un dénominateur, tu peux lire la fiche La représentation d'une fraction.

Il faut bien s’assurer que les touts sont identiques, c’est-à-dire de la même grosseur, comme c'est le cas dans l'image suivante.

Sur cette image, tu peux aussi voir qu'utiliser |2| parties sur |3,| c’est équivalent à utiliser |4| parties sur |6| ou |8| parties sur |12.| La quantité utilisée représente donc la même partie du tout.

Pour trouver une fraction équivalente à l'aide de la multiplication, je dois suivre les étapes suivantes :

1. Je détermine par quel nombre je veux multiplier la fraction. 

2. Je multiplie le numérateur par ce nombre.

3. Je multiplie le dénominateur par ce même nombre.

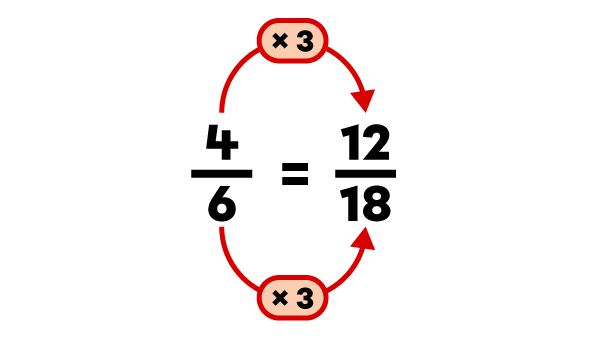
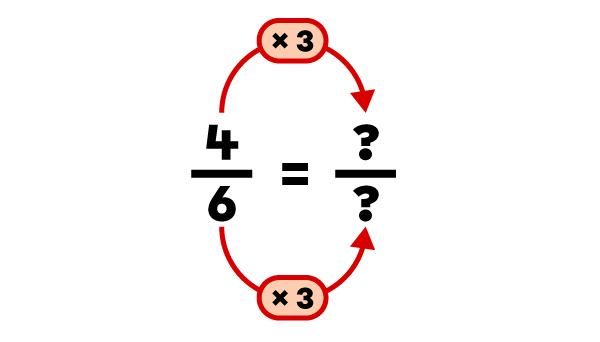
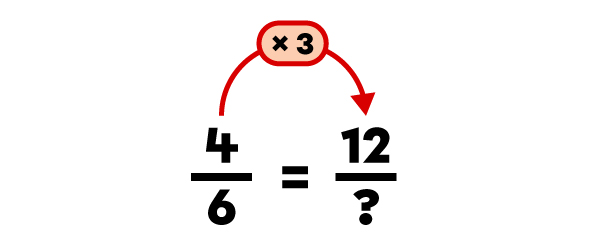
Trouve une fraction équivalente à |\dfrac{4}{6}| à l’aide de la multiplication.

Je détermine par quel nombre je veux multiplier la fraction.  Je choisis de multiplier la fraction par |3| .
Je multiplie le numérateur par ce nombre.
Je multiplie le dénominateur par ce même nombre.

|\dfrac{12}{18}| est une fraction équivalente à |\dfrac{4}{6}.|

Pour trouver une fraction équivalente à l'aide de la division, je dois suivre les étapes suivantes :

1. Je détermine par quel nombre je veux diviser la fraction. 

2. Je divise le numérateur par ce nombre.

3. Je divise le dénominateur par ce même nombre. 

Trouve une fraction équivalente à |\dfrac{4}{6}| à l’aide de la division.

Je détermine par quel nombre je veux diviser la fraction.  Je dois m'assurer que le numérateur et le dénominateur se divisent par le nombre choisi. Je sais que |4| et |6| se divisent par |2.|
Je divise le numérateur par ce nombre.
Je divise le dénominateur par ce même nombre.

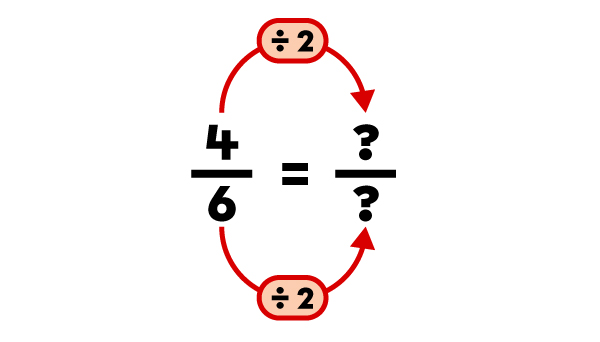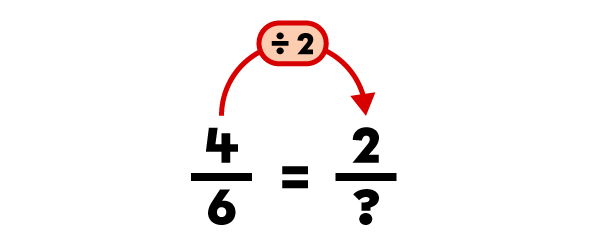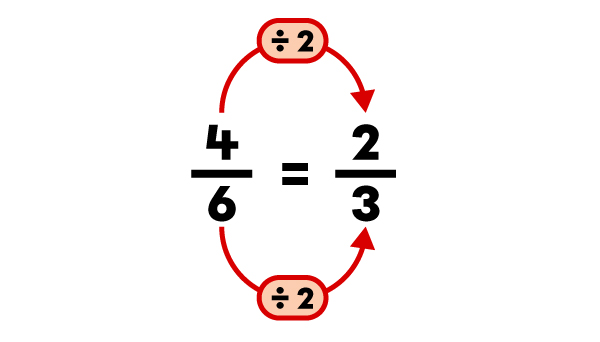|\dfrac{2}{3}| est une fraction équivalente à |\dfrac{4}{6}.|