Les formules qui permettent de calculer l'aire et le volume du cône sont différentes de celles qu'on utilise pour les pyramides étant donné que le cône fait partie des corps ronds. Quand on jette un coup d'œil à son développement, on remarque que la base est formée d’un disque et que la face latérale est formée d’un secteur de disque.
La base d'un cône est formée d'un disque. La formule permettant de calculer l'aire de ce disque est la suivante.
||A_b = \pi r^2|| où ||\begin{align}A_b&:\text{Aire de la base}\\r &: \text{rayon}\end{align}||
Lorsqu’on a la mesure du rayon, on applique cette formule pour déterminer la superficie de la base.
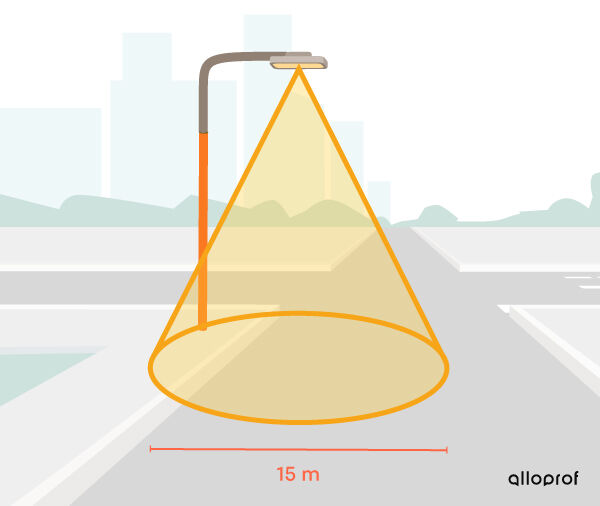
Afin de s'assurer qu'un espace de stationnement soit bien éclairé, détermine la superficie couverte au sol par la lumière du lampadaire.
-
Identifier la face concernée
Dans ce cas, comme pour tous les cônes circulaires droits, la base est un disque. -
Appliquer la formule ||\begin{align} A_b &= \pi r^2\\ &= \pi \left(\dfrac{15}{2}\right)^2\\ &= 56{,}25\pi \\ &\approx 176{,}71 \ \text{m}^2\end{align}||
-
Interpréter la réponse
La surface éclairée par le lampadaire a une superficie d'environ |176{,}71 \ \text{m}^2.|
Même si la formule peut paraitre simple à appliquer, il faut s'assurer d'avoir les bonnes mesures pour l'utiliser. Ici, le |15\ \text{m}| fait référence au diamètre et non au rayon. Pour obtenir la mesure voulue, il faut diviser cette mesure par |2.|
En raison de son développement assez particulier, il peut paraitre difficile de résumer le calcul de l'aire latérale du cône en une seule formule. Or, les différentes propriétés de ce dernier permettent tout de même d’en déduire la formule suivante.
||A_L = \pi r a|| où ||\begin{align} A_L&:\text{Aire latérale}\\r &: \text{rayon de la base}\\ a &: \text{apothème du cône}\end{align}||
Pour estimer la quantité de tissu à utiliser pour confectionner une robe, on peut avoir recours à la représentation du cône.
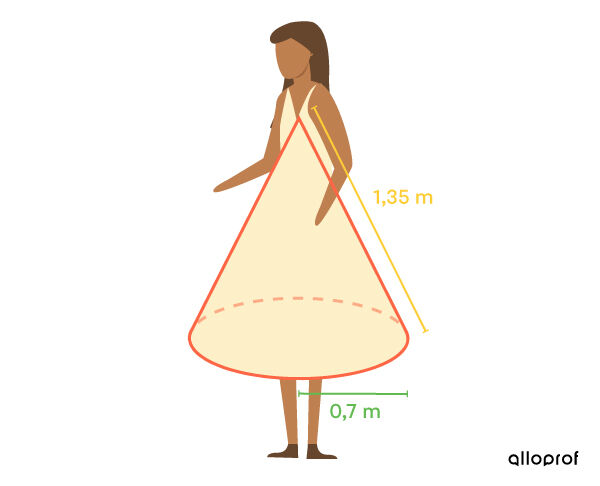
En sachant que cette robe est confectionnée avec de la soie et que ce matériau coute |12\ $ /\text{m}^2,| combien devrait-on débourser pour acheter suffisamment de tissu?
-
Identifier le solide
Cette robe de forme conique n'est pas fermée dans le bas. Il ne faut calculer que l’aire latérale de celle-ci. -
Appliquer la formule ||\begin{align} A_L &= \pi r a\\ &= \pi (0{,}7) (1{,}35)\\ &= 0{,}945\pi \\ &\approx 2{,}97 \ \text{m}^2\end{align}||
-
Interpréter la réponse
Puisqu'il se vend |12$ / \text{m}^2,| on utilise la multiplication : ||2{,}97\ \text{m}^2 \times 12\ $/\text{m}^2 = 35{,}64\ $|| Ainsi, on pourrait obtenir le tissu à un prix de |35{,}64\ $.|
Dans plusieurs cas où des surfaces courbes sont mises en contexte, il ne faut pas oublier que cet exemple présente une estimation et non une quantité exacte.
Il faut faire le développement d’un cône et identifier ses différents côtés remarquables.
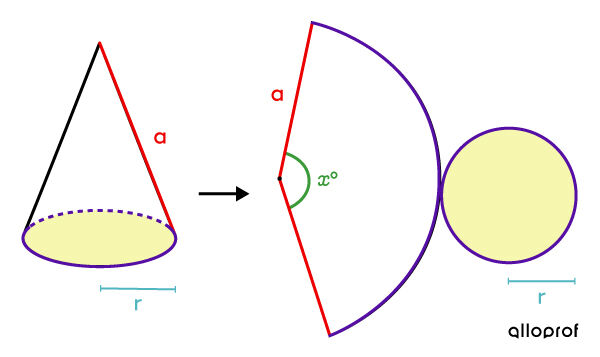
De cette façon, on peut voir différents liens avec les propriétés du cercle, des angles au centre et des secteurs d'un disque.
Dans ce cas, l'aire latérale du cône est en fait l'aire du secteur du disque créé avec le rayon |\color{#EC0000}{a}| qu'on peut représenter à l’aide de la proportion suivante : ||\begin{align} \dfrac{\text{Aire du secteur}}{\text{Aire du disque}} &= \dfrac{\color{#3A9A38}{\text{Angle au centre}}}{360^\circ} \\\\\dfrac{\text{Aire du secteur}}{\pi \color{#EC0000}{a}^2} &= \dfrac{\color{#3A9A38}{x^\circ}}{360^\circ}\\\\ \Rightarrow\ \text{Aire du secteur} &= \dfrac{\pi \color{#EC0000}{a}^2 \color{#3A9A38}{x}}{360}\end{align}||
On peut également exprimer la mesure de l'angle au centre selon l'arc de cercle qu'il définit. Par sa construction, cet arc de cercle correspond à la circonférence de la base, ce qui permet d’en déduire que :
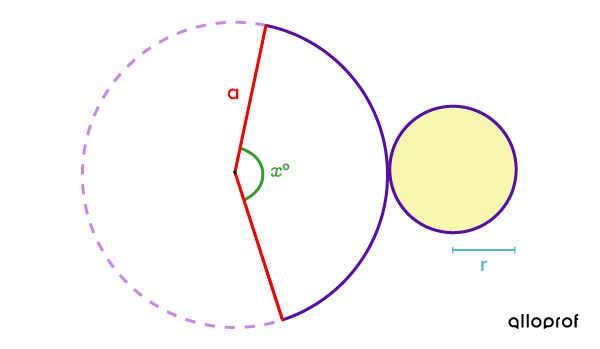
||\begin{align} \dfrac{\color{#3A9A38}{\text{Angle au centre}}}{360^\circ} &= \dfrac{\color{#560FA5}{\text{Arc de cercle}}}{\color{#C58AE1}{\text{Circonférence}}} \\\\ \dfrac{\color{#3A9A38}{x}^\circ}{360^\circ} &= \dfrac{\color{#560FA5}{\text{Arc de cercle}}}{\color{#C58AE1}{\text{Circonférence}}} \\\\ \dfrac{\color{#3A9A38}{x}^\circ}{360^\circ} &= \dfrac{2 \pi \color{#51B6C2}{r}}{2 \pi \color{#EC0000}{a}}\\\\ \Rightarrow\ \color{#3A9A38}{x} &= \dfrac{360 \times 2 \pi \color{#51B6C2}{r}}{2 \pi \color{#EC0000}{a}} \\\\ \color{#3A9A38}{x} &= \dfrac{360 \color{#51B6C2}{r}}{\color{#EC0000}{a}}\end{align}||
En substituant l'expression algébrique associée à |\color{#3A9A38}{x},| on obtient : ||\begin{align} \text{Aire du secteur}&= \dfrac{\pi \color{#EC0000}{a}^2 \color{#3A9A38}{x}}{360^\circ}\\\\ &= \dfrac{\pi \color{#EC0000}{a}^2 \left(\dfrac{360 \color{#51B6C2}{r}}{\color{#EC0000}{a}}\right)}{360}\\\\ &= \dfrac{360\pi \color{#51B6C2}{r} \color{#EC0000}{a}}{360}\\\\ &= \pi \color{#51B6C2}{r} \color{#EC0000}{a}\end{align}|| Puisque l'aire du secteur est en fait l'aire latérale, alors :||A_L = \pi \color{#51B6C2}{r} \color{#EC0000}{a}||
Chaque fois qu'il est question d'aire totale, il faut prendre en considération toutes les faces du solide et faire la somme de leur superficie respective.
||A_T = A_L + A_b|| où ||A_T:\text{Aire totale}||
L'aire de la base n'est considérée qu'une seule fois puisqu'il n'y a qu'une seule figure qui sert de base dans un cône.
Au début de l’année 1973, le groupe de musique désormais légendaire du nom de Kiss a fait son entrée dans l’industrie du spectacle. Pour se distinguer, les membres du groupe ont pris la décision de s'habiller d'une façon assez particulière. Entre autres, un des membres a décidé d'intégrer des pointes de forme conique à son costume.
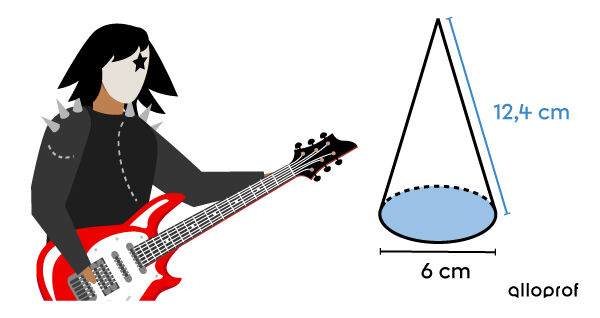
Pour les faire fabriquer, il a besoin de déterminer l'aire totale de chacune de ces pointes. Selon les mesures qui sont fournies, détermine cette aire totale.
-
Identifier les faces concernées
Il est mentionné que ce sont toutes les faces du cône qui sont à considérer. -
Calculer l'aire de la base ||\begin{align} A_b &= \pi r^2\\ &= \pi \left(\dfrac{6}{2}\right)^2\\ &= 9\pi \\ &\approx 28{,}27 \ \text{cm}^2\end{align}||
-
Calculer l'aire latérale ||\begin{align} A_L &= \pi r a\\ &= \pi \left(\dfrac{6}{2}\right)(12{,}4)\\ &= 37{,}2\pi \\ &\approx 116{,}87 \ \text{cm}^2\end{align}||
-
Calculer l'aire totale ||\begin{align} A_T &= A_L + A_b\\ &= 37{,}2\pi + 9\pi\\ &= 46{,}2\pi \\ &\approx 145{,}14 \ \text{cm}^2\end{align}||
-
Interpréter la réponse
L'aire totale d'une pointe de son costume est d'environ |145{,}14 \ \text{cm}^2.|
Dans d'autres circonstances, on pourrait s'intéresser à la mesure d’une dimension de la base ou encore de l’apothème du cône alors que l’aire totale est donnée, c’est ce qu’on appelle trouver une mesure manquante d'un cône à partir de l'aire. Dans ce cas, la démarche est un peu différente, mais il demeure essentiel de se rappeler la formule de l’aire totale associée aux cônes.
Malgré toutes les formules, il peut arriver que certaines données soient manquantes. Dans ce cas, il faut utiliser d'autres concepts mathématiques afin d'obtenir le résultat recherché. Par exemple, la mesure de l’apothème n’est pas toujours directement donnée. Le théorème de Pythagore est alors souvent utilisé.
Dans le cas d'un cône droit, on peut obtenir un triangle rectangle en traçant l’apothème du cône, la hauteur du cône et un rayon de la base.

Puisque c’est un cône droit, la hauteur intercepte perpendiculairement le centre de la base. Ainsi, la mesure de la cathète correspond au rayon de la base.
En associant la mesure d'une cathète à celle du rayon de la base, l'autre cathète à celle de la hauteur du cône et l'apothème, à celle de l'hypoténuse, on a assez d'informations pour utiliser le théorème de Pythagore : ||\begin{align} \color{#3A9A38}{a}^2 + \color{#EC0000}{b}^2&= \color{#51B6C2}{c}^2\\\\ \color{#3A9A38}{4}^2 + \color{#EC0000}{12}^2 &= \color{#51B6C2}{a}^2\\ 160 &= \color{#51B6C2}{a}^2 \\12{,}65 \ \text{cm} &\approx \color{#51B6C2}{a} \end{align}|| L’apothème du cône mesure environ |12{,}65\ \text{cm}.|
Lorsqu'on utilise plusieurs concepts simultanément, il faut faire attention de ne pas se perdre dans l'utilisation des variables. Sur le cône, |\color{#51B6C2}{a}| fait référence à l'apothème, alors que dans le théorème de Pythagore, c'est la variable |\color{#51B6C2}{c}| qui fait référence à ce segment. Pour bien comprendre le dernier exemple, l'utilisation des couleurs aide beaucoup à associer les nombres aux segments qu'ils représentent.
Si tu cherches la mesure de la hauteur à partir de l'apothème, c’est encore le théorème de Pythagore qu’il faut utiliser.