Pour répondre à différents besoins, il peut arriver qu'un seul solide ne soit pas suffisant. Dans ce cas, on peut être tenté de combiner plusieurs solides ou d'en altérer un.
Un solide décomposable est un solide pouvant être séparé en plusieurs solides plus simples.
Comme le mentionne la définition, il s'agit simplement de reconnaitre les divers solides utilisés pour le construire.
En résumé, un solide décomposable doit posséder les caractéristiques suivantes :
-
Il doit être formé d'au moins deux solides.
-
Les solides utilisées doivent avoir une face ou une section de face commune.
-
Il peut être formé de polyèdres et de corps ronds simultanément.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>En respectant ces caractéristiques, les combinaisons possibles<span><span> pour former un solide décomposable</span></span> sont illimitées.</p>
<p>En reconnaissant les différents solides utilisés, il devient plus facile de <a href="/fr/eleves/bv/mathematiques/l-aire-et-le-volume-des-solides-decomposables-con-m1513">calculer l'aire et le volume</a>. On peut également créer de nouveaux solides non pas en ajoutant des solides, mais en y retirant des sections.</p>
</body></html>
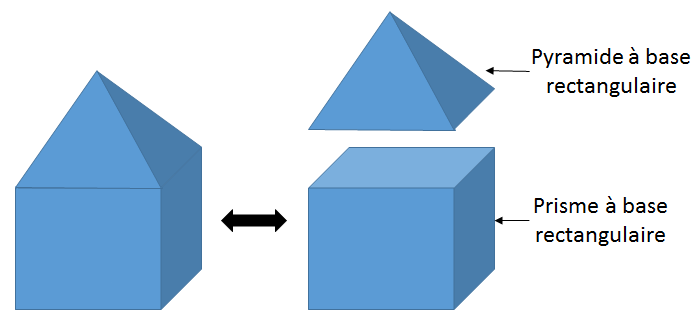
Un empilement de blocs de bois (à gauche) correspond à un solide décomposable. Le solide de droite est formé par la combinaison d'une pyramide et d'un prisme.
Un solide tronqué est un solide qui a été coupé par un plan et dont seulement une portion de la séparation est conservée.
Dans le cas présent, l'expression « une image vaut mille mots » prend tout son sens. Au lieu d'énumérer les différentes caractéristiques de construction de ces solides, voici quelques exemples.
Polyèdre tronqué par un seul plan
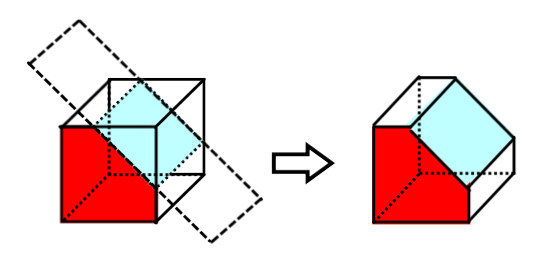
Polyèdre tronqué par plusieurs plans
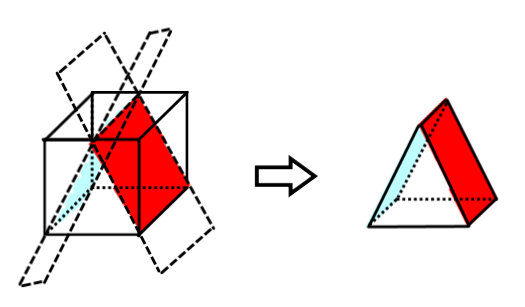
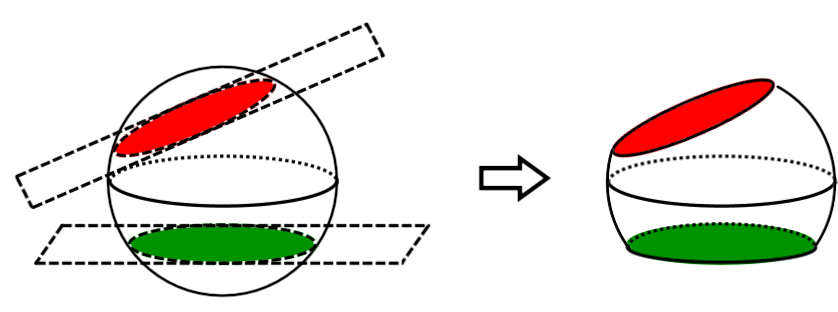
Corps rond tronqué par un plan
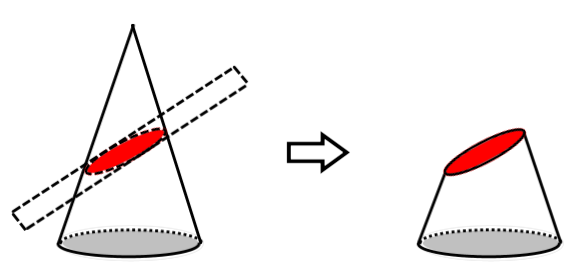
Corps rond tronqué par plusieurs plans
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Ainsi, on peut voir que certains solides tronqués possèdent des noms et des caractéristiques précises comme le prisme à base triangulaire (deuxième dessin). Pour les autres, on utilisera l'addition et la soustraction pour combiner différentes formules afin de calculer <a href="/fr/eleves/bv/mathematiques/l-aire-et-le-volume-des-solides-tronques-m1514">leur aire et leur volume</a>.</p>
</body></html>
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Par ailleurs, il faut faire attention pour ne pas confondre un solide tronqué avec <a href="/fr/eleves/bv/mathematiques/les-polyedres-m1229">un solide non convexe</a>. En résumé, il y a une différence entre scinder un solide avec un plan ou enlever une portion d'un solide à l'intérieur de celui-ci.</p>
</body></html>
