Pour réussir à calculer une mesure manquante à partir de l'aire dans un solide décomposable ou dans un solide tronqué, les formules d'aire des figures planes sont utiles. La démarche est un peu plus complexe que pour les solides simples comme les prismes et les pyramides étant donné que la quantité de figures planes utilisées dans la construction d'un solide décomposable est plus grande. Pour faciliter ta compréhension des exemples qui suivent, voici une représentation globale de la démarche utilisée.
-
Déterminer l'aire avec laquelle il faut travailler.
-
Identifier la (ou les) mesure(s) manquante(s) à l'aide d'une variable.
-
Associer à l'aire de chaque figure une valeur numérique ou une expression algébrique.
-
Créer une équation en fonction du contexte.
-
Résoudre l'équation.
-
Interpréter la réponse selon le contexte.
Afin d'augmenter sa visibilité, une compagnie qui travaille dans le domaine animalier veut mettre sur le marché un nouveau jouet pour chien. Pour s'assurer de susciter de l'intérêt envers cette nouveauté, elle pense recouvrir le jouet d'un produit possédant une odeur et un gout que les chiens aiment.
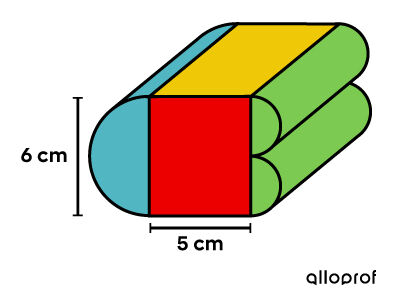
Après quelques appels, la compagnie trouve un fournisseur qui est prêt à lui vendre un tel produit au cout de |0{,}02\ $ / \text{cm}^2| de surface à couvrir. Pour maximiser ses profits, la compagnie sait qu'elle doit investir |9{,}20\ $| pour recouvrir chaque jouet de ce produit.
Ainsi, pour respecter cet investissement, quelle devrait être la longueur du jouet?
-
Déterminer l'aire avec laquelle il faut travailler
On doit résoudre une proportion pour trouver la surface totale du jouet. ||\begin{align} \dfrac{0{,}02\ $}{1 \ \text{cm}^2} &= \dfrac{9{,}20\ $}{\text{Aire totale}} \\\\ \text{Aire totale} &= \dfrac{ 9{,}20\times 1}{0{,}02}\\ &= 460\ \text{cm}^2\end{align}|| -
Identifier la mesure manquante à l'aide d'une variable
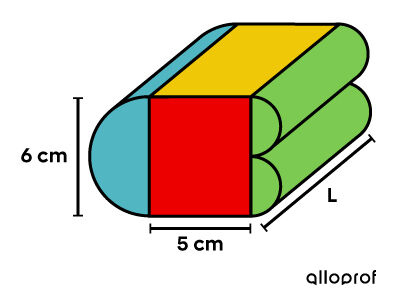
-
Associer à l'aire de chaque figure une valeur numérique ou une expression algébrique
||\begin{align} \color{#ec0000}{A_\text{rectangles}} &= (5 \times 6) \times 2\\ &= \color{#ec0000}{60 }\\\\ \color{#EFC807}{A_\text{rectangles}} &= (5 \times L) \times 2\\ &= \color{#EFC807}{10L}\\\\ \color{#51B6C2}{A_\text{demi-cylindre}} &= \dfrac{\pi (6 \div 2)^2} {2} \times 2+ \left( \dfrac{6 \pi }{2}\right) \times L\\ &\approx \color{#51B6C2}{28{,}27 + 9{,}42 L}\\\\ \color{#7CCA51}{A_\text{2 demi-cylindres}} &= \dfrac {\pi (6 \div 4)^2}{2} \times 4 + \dfrac{\pi (6 \div 2)}{2} \times L \times 2\\ &\approx \color{#7CCA51}{14{,}14 + 9{,}42 L}\end{align}|| -
Créer une équation en fonction du contexte
||\begin{align} \text{Aire totale} &= \text{Somme des aires de toutes les surfaces}\\ 460 &= \color{#ec0000}{60} + \color{#EFC807}{10L} + \color{#51B6C2}{28{,}27 + 9{,}42L} + \color{#7CCA51}{14{,}14 + 9{,}42L}\\ 460 &= 28{,}84 L + 102{,}41\end{align}|| -
Résoudre l'équation
||\begin{align}460 \color{#ec0000}{-102{,}41} &= 28{,}84L + 102{,}41 \color{#ec0000}{-102{,}41} \\ \color{#ec0000}{\dfrac{\color{black}{357{,}59}}{28{,}84}} &= \color{#ec0000}{\dfrac{\color{black}{28{,}84L}}{28{,}84}}\\ 12{,}40 &\approx L\end{align}|| -
Interpréter la réponse selon le contexte
La longueur du jouet devrait être d'environ |12{,}40\ \text{cm}.|
De façon générale, il s'agit de bien identifier l'inconnue pour ensuite utiliser les formules adéquates afin de créer une équation qui résume la situation. Une fois l'équation résolue, il ne reste qu'à interpréter la réponse.
Pour trouver les mesures manquantes à partir de l'aire dans des solides complexes avec des équations de degré 2, la démarche à suivre est relativement semblable à celle qui implique des équations de degré 1. Par contre, les méthodes de résolution utilisées à l'étape 5 sont un peu différentes. Généralement, on peut s'en remettre à la factorisation par la méthode produit-somme ou à l'utilisation de la formule quadratique.
Une compagnie se spécialise dans la fabrication de crampons. Pour répondre à sa plus récente demande, elle doit construire un crampon qui a l'allure suivante :
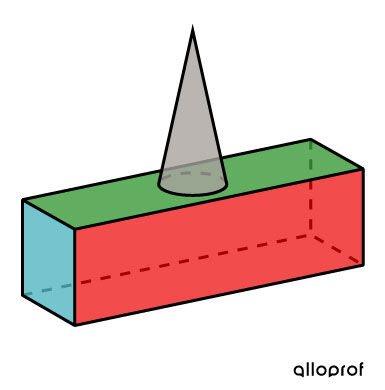
La demande exige également certaines spécifications particulières.
-
La longueur de la base doit mesurer |10\ \text{mm}| de plus que l'apothème du cône;
-
La largeur de la base doit mesurer |4\ \text{mm}| de moins que l'apothème du cône;
-
La hauteur du prisme doit mesurer exactement |6\ \text{mm};|
-
La mesure du rayon du cône doit être d'exactement |2\ \text{mm};|
-
L'aire totale d'un crampon doit être de |600\ \text{mm}^2.|
Quelles doivent être les mesures précises de chacune des dimensions de ce crampon qui respectent les contraintes?
-
Déterminer l'aire avec laquelle il faut travailler
Il est mentionné que l'aire totale doit être de |600\ \text{mm}^2.| -
Identifier les mesures à l'aide d'une variable ou d'une expression algébrique

-
Associer à l'aire de chaque figure une valeur numérique ou une expression algébrique
||\begin{align} \color{#51B6C2}{A_\text{rectangles}} &= \big((x-4) \times 6\big) \times 2\\ &=(6x-24)\times 2\\ &= \color{#51B6C2}{12x - 48}\\\\ \color{#ec0000}{A_\text{rectangles}} &= \big((x+10) \times 6\big)\times 2\\ &=(6x+60)\times 2\\ &= \color{#ec0000}{12x + 120}\\\\ A_\text{rectangle du dessous} &= (x+10)\times (x-4)\\ &=x^2+10x-4x-40\\ &= x^2 + 6x - 40\\\\ \color{#3A9A38}{A_\text{rectangle}} &= (x+10) \times (x-4) - \pi (2)^2\\ &= x^2-4x+10x-40 - 4\pi\\ &\approx \color{#3A9A38}{x^2 + 6x-52{,}57}\\\\ \color{#a8a39e}{A_\text{cône}} &= \pi r a\\ &= \pi \times 2 \times x\\ &=2\pi x\\ &\approx\color{#a8a39e}{6{,}28x} \end{align}|| -
Créer une équation
||\begin{align} \text{Aire totale} &= \text{Somme de l’aire de chacune des surfaces}\\ 600 &= \color{#51B6C2}{12x-48} + \color{#ec0000}{12x+120} + x^2 + 6x - 40 + \color{#3A9A38}{x^2+6x-52{,}56} +\color{#a8a39e}{6{,}28x}\end{align}|| -
Résoudre l'équation
||\begin{align} 600 &= 2x^2+42{,}28x -20{,}26\\ 0 &= 2x^2+42{,}28x - 620{,}26\\\\ \{x_1, x_2\} &= \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\\\ \{x_1, x_2\} &= \frac{-(42{,}28) \pm \sqrt{42{,}28^2-4 (2)(-620{,}26)}}{2 \times 2}\\\\ x_1 &\approx -31{,}11 \ \text{et} \ x_2 \approx 9{,}97\end{align}|| -
Interpréter la réponse selon le contexte
Puisqu'on cherche une mesure de longueur, on considère seulement la valeur positive, soit |x_2 \approx 9{,}97.|
Ainsi, les dimensions recherchées sont les suivantes : ||\begin{align} \text{Longueur} &= x+10\\ &=9{,}97+10\\ &= 19{,}97\ \text{mm}\\\\ \text{Largeur} &= x-4\\ &=9{,}97-4\\ &= 5{,}97\ \text{mm}\\\\ \text{Apothème} &= x\\ &=9{,}97\ \text{mm} \end{align}||
Étant donné sa construction particulière, un solide tronqué peut souvent être associé à un solide décomposable. En fait, il s'agit plutôt d'un solide auquel on a enlevé une partie. Dans certains cas, il faut établir une proportion entre les mesures du solide entier et celles de la partie tronquée. C’est ce qui est fait avec le cône tronqué dans l’exemple qui suit. Dans d'autres cas, il suffit d'analyser chacune des faces du solide et de les décomposer de façon appropriée pour retrouver des polygones connus.
Le bouchon de caoutchouc suivant a une aire totale de 105,61 cm2. Quelle est la hauteur du bouchon si le diamètre du petit disque est de 4 cm et celui du grand, de 6 cm? Le bouchon est un tronc de cône dont les 2 bases sont des disques parallèles.
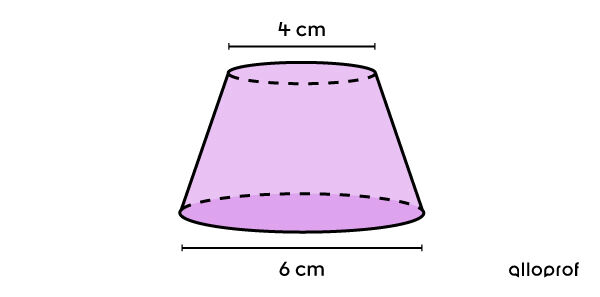
-
Déterminer la mesure de l'aire
L'aire totale est donnée clairement : |\text{A}_{\text{totale}}=105{,}61\ \text{cm}^2.| -
Identifier les mesures manquantes
Pour bien visualiser la situation, on représente le cône en entier.
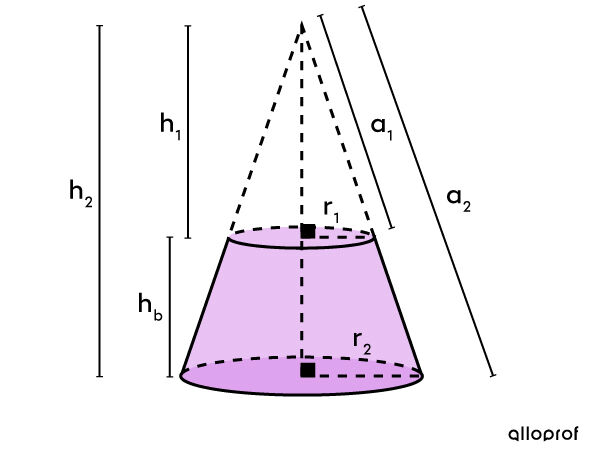
Il y a plusieurs mesures manquantes, soit la hauteur du cône tronqué |(h_1),| l'apothème du cône tronqué |(a_1),| la hauteur du cône complet |(h_2),| l'apothème du cône complet |(a_2)| et la hauteur du bouchon |(h_b).| Il faut associer la variable |x| à l'une ou l'autre de ces inconnues. Ici, on suppose que |x=a_1.|
On trouve les 2 rayons.
|| \begin{align}r_1 = 4\ \text{cm} \div 2 = 2\ \text{cm}\\
r_2 = 6\ \text{cm} \div 2 = 3\ \text{cm} \end{align}||
Dans un cône tronqué, comme dans une pyramide tronquée, les mesures des côtés homologues sont proportionnelles.
||\dfrac{\text{rayon}_1}{\text{rayon}_2} = \dfrac{\text{apothème}_1}{\text{apothème}_2} = \dfrac{\text{hauteur}_1}{\text{hauteur}_2}||
||\begin{align} \dfrac{r_1}{r_2}&=\dfrac{a_1}{a_2}\\\\ \dfrac{2}{3}&=\dfrac{x}{a_2}\\\\ \Rightarrow\ a_2&=\dfrac{3x}{2}\\ &=1{,}5x \end{align}||
-
Associer à l'aire de chaque figure une valeur numérique ou une expression algébrique
||\begin{align}A_{\text{petite base}}&=\pi r_1^2\\&=\pi (2)^2\\ &=4\pi \end{align}|| ||\begin{align}A_{\text{grande base}}&=\pi r_2^2\\&=\pi (3)^2\\ &=9\pi \end{align}|| Pour calculer l'aire latérale du tronc de cône |(A_{\text{L tronc}}),| il faut soustraire l'aire latérale du cône tronqué |(A_{L1})| à l'aire latérale du cône entier |(A_L2).| ||\begin{align}A_{L1}&=\pi r_1a_1\\&=\pi (2) (x)\\&\approx6{,}28x \end{align}|| ||\begin{align}A_{L2}&=\pi r_2a_2\\&=\pi (3) (1{,}5x)\\&\approx14{,}14x \end{align}|| ||\begin{align}A_{L\ \text{tronc}}&=A_{L2}-A_{L1}\\&=4{,}5\pi x - 2\pi x\\&=2{,}5\pi x\\&\approx7{,}85x \end{align}|| -
Créer une équation en fonction du contexte
||\begin{align}A_{\text{L tronc}}&=A_{\text{bouchon}}-A_{\text{petite base}}-A_{\text{grande base}}\\2{,}5 \pi x &=105{,}61-4\pi-9\pi \\ 2{,}5 \pi x &\approx 64{,}77 \end{align}|| -
Résoudre l'équation
||\begin{align} \color{#ec0000}{\dfrac{\color{black}{2{,}5 \pi x}}{2{,}5\pi}} &\approx \color{#ec0000}{\dfrac{\color{black}{64{,}77}}{2{,}5\pi}} \\ x &\approx 8{,}25\ \text{cm} = a_1 \end{align}|| -
Interpréter la réponse selon le contexte
Maintenant qu'on a déterminé la valeur de |x,| on doit utiliser cette mesure pour calculer la hauteur de la pyramide tronquée |(h_1).| On utilise le théorème de Pythagore dans le triangle rectangle formé par |a_1,| |h_1| et |r_1.| ||\begin{align} {h_1}^2 &= {a_1}^2 - {r_1}^2 \\ h_1 &= \sqrt{8{,}25^2 - 2^2}\\ h_1 &\approx 8\ \text{cm} \end{align}|| Pour calculer |h_2,| on peut réutiliser le fait que les mesures des côtés homologues sont proportionnelles. ||\begin{align} \dfrac{r_1}{r_2} &= \dfrac{h_1}{h_2} \\\\ \dfrac{2}{3} &= \dfrac{8}{h_2} \\\\ \Rightarrow\ h_2 &= \dfrac{3\times 8}{2} \\ h_2 &= 12\ \text{cm} \end{align}|| Il ne reste plus qu'à donner la hauteur du bouchon : ||\begin{align}h_b&=h_2-h_1\\ &=12-8\\&=4\ \text{cm}\end{align}||
Le prochain exemple présente une situation avec un prisme tronqué.
Pour rénover son immeuble à logements, un propriétaire décide de remplacer le revêtement extérieur et de changer la structure du toit. Au lieu d'avoir un toit plat, il veut en avoir un incliné sur deux faces.
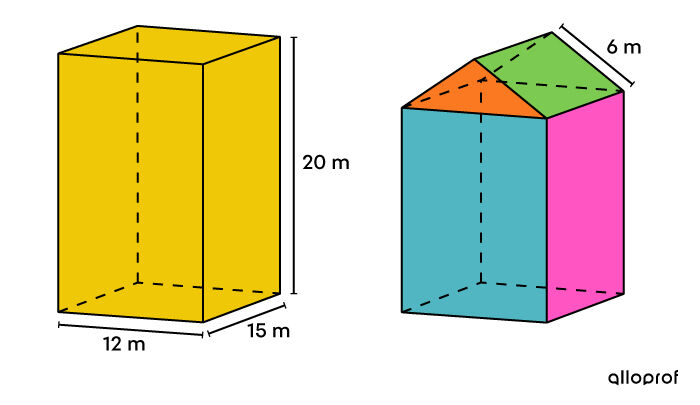
Pour assumer les couts du nouveau revêtement, il dispose d'un budget de | 30\ 000\ $| et le matériau qu'il veut utiliser se vend |27{,}70\ $ / \text{m}^2.| Ainsi, quelle devrait être la hauteur de son nouveau toit qui est incliné sur 2 faces?
-
Déterminer la mesure de l'aire
||\begin{align} \text{Aire totale} &= 30\ 000\ $ \div 27{,}70 \ $/\text{m}^2 \\ &\approx 1 \ 083{,}03 \ \text{m}^2 \end{align}|| -
Identifier la mesure manquante
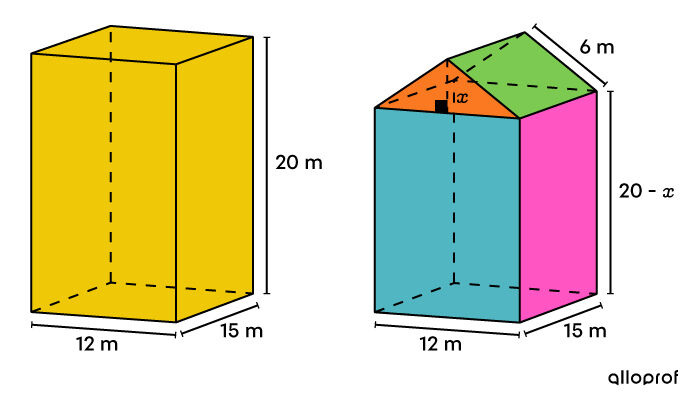
-
Trouver l'aire de chacune des surfaces
||\begin{align} \color{#51B6C2}{A_\text{rectangles}} &= \big(12 (20-x)\big) \times 2 \\ &= \color{#51B6C2}{480 - 24x} \\\\ \color{#ff55c3}{A_\text{rectangles}} &= \big(15 (20-x)\big)\times 2 \\ &= \color{#ff55c3}{600 - 30x} \\\\ \color{#FA7921}{A_\text{triangles}} &= \left(\dfrac{12 \times x}{2}\right) \times 2 \\ &= \color{#FA7921}{12x}\\\\ \color{#7CCA51}{A_\text{rectangles}} &= (6 \times 15) \times 2\\ &= \color{#7CCA51}{180} \end{align}|| -
Créer une équation en fonction du contexte
||\begin{align} \text{Aire totale} &= \text{Somme des aires de chacune des faces}\\ 1 \ 083{,}03 &= \color{#51B6C2}{480 - 24x} + \color{#ff55c3}{600 - 30x} + \color{#FA7921}{12x} + \color{#7CCA51}{180}\end{align}|| -
Résoudre l'équation
||\begin{align} 1 \ 083{,}03 &= 1\ 260 - 42x \\ 1 \ 083{,}03 \color{#ec0000}{-1\ 260} &= 1\ 260 \color{#ec0000}{-1\ 260} - 42x \\ \color{#ec0000}{\dfrac{\color{black}{-176{,}97}}{-42}} &= \color{#ec0000}{\dfrac{\color{black}{-42x}}{-42}} \\ 4{,}21 &\approx x \end{align}|| -
Interpréter la réponse selon le contexte
La hauteur de son toit devrait être d'environ |4{,}21 \ \text{m}.|
Puisqu'on travaille en 3 dimensions, il peut arriver qu'il y ait des sections de solide manquantes ou cachées. Dans ce cas, on peut décomposer le solide non convexe selon les différentes figures planes qui le composent.
La démarche pourrait ressembler à la suivante.
En guise de passetemps, Mylène offre ses services afin de cuisiner des gâteaux personnalisés. Pour respecter le budget de son dernier client, elle sait qu'il lui reste 11 $ à investir dans l'application du glaçage.
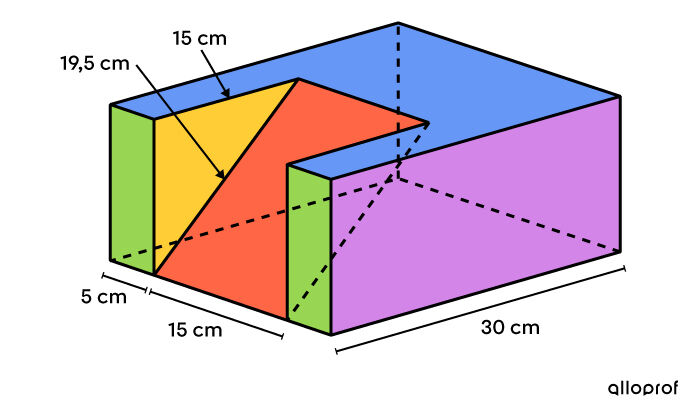
Sachant qu'il lui en coute |0{,}50\ $ / \text{dm}^2| pour se procurer les ingrédients nécessaires, quelle devrait être la hauteur du gâteau?
-
Déterminer la mesure de l'aire
||\begin{align} \dfrac{0{,}5\ $}{1\ \text{dm}^2} &= \dfrac{11\ $}{?\ \text{dm}^2} \\\\ ? &= \dfrac{11\times 1}{0{,}5} \\ &= 22\ \text{dm}^2 \\ &= 2\ 200\ \text{cm}^2\end{align}|| -
Identifier la mesure manquante à l'aide d'une variable

-
Trouver l'aire de chacune des surfaces
Avant de calculer l’aire de toutes les faces, il est important de se rappeler le contexte. Comme il s’agit d’un gâteau, on ne met pas de glaçage en dessous. Ainsi, on ne calcule pas l’aire du rectangle du dessous. ||\begin{align} \color{#3B87CD}{A_\text{dessus}} &= (5 \times 15) \times 2 + (30-15) (5 + 15 + 5) \\ &= 150 + 375\\ &= \color{#3B87CD}{525 \ \text{cm}^2} \\\\ \color{#7CCA51}{A_\text{rectangles}} &= (5 \times x) \times 2 \\ &= \color{#7CCA51}{10 x} \\\\ A_\text{rectangle de derrière} &= (5 + 15 + 5) \times x \\ &= 25x \\\\ \color{#C58AE1}{A_\text{rectangles}} &= (30 \times x) \times 2 \\ &= \color{#C58AE1}{60x} \\\\ \color{#EFC807}{A_\text{triangles}} &= \left(\dfrac{15 \times x}{2}\right) \times 2 \\ &= \color{#EFC807}{15x}\\\\ \color{#ec0000}{A_\text{rectangle}} &= 15 \times 19{,}5 \\ &= \color{#ec0000}{292{,}5\ \text{cm}^2} \end{align}|| -
Créer une équation en fonction du contexte
||\begin{align} \text{Aire totale} &=\text{Somme des aires de chacune des faces}\\ 2 \ 200 &=\color{#3B87CD}{525} + \color{#7CCA51}{10x} + 25x + \color{#C58AE1}{60x} + \color{#EFC807}{15x} + \color{#ec0000}{292{,}5}\end{align}|| -
Résoudre l'équation
||\begin{align} 2 \ 200 &= 110x + 817{,}57 \\ 2 \ 220 \color{#ec0000}{-817{,}57} &= 110x +817{,}57 \color{#ec0000}{-817{,}57} \\ \color{#ec0000}{\dfrac{\color{black}{1\ 382{,}43}}{110}} &= \color{#ec0000}{\dfrac{\color{black}{110x}}{110}} \\ 12{,}57 &\approx x \end{align}|| -
Interpréter la réponse selon le contexte
Ainsi, le gâteau devrait avoir une hauteur d'environ |12{,}57 \ \text{cm}.|
Pour valider ta compréhension à propos des mesures manquantes dans les solides de façon interactive, consulte la MiniRécup suivante :
