La corrélation est un lien entre 2 variables quantitatives d'une distribution qui décrit le type, le sens et la force de ce lien.
Dans un nuage de points, chaque point représente une paire de valeurs pour les 2 variables mesurées. La corrélation est alors visible à travers la forme générale du nuage de points. Par exemple, si les points semblent alignés, cela indique une forte corrélation linéaire. Si les points sont dispersés de manière aléatoire, cela indique une faible corrélation ou même une absence de corrélation.
Il est possible de superposer une droite de régression linéaire sur le nuage de points pour visualiser la tendance de la corrélation. La droite de régression linéaire est une ligne qui passe au plus près des points et qui permet de prédire la valeur d'une variable en fonction de la valeur de l'autre variable.
Il existe 2 types de corrélation : la corrélation positive et la corrélation négative.
-
La corrélation positive indique que les 2 variables ont tendance à évoluer dans le même sens, c'est-à-dire que lorsqu'une variable augmente, l'autre variable augmente aussi, et vice versa.
-
La corrélation négative indique que les 2 variables ont tendance à évoluer dans le sens contraire, c'est-à-dire que lorsqu'une variable augmente, l'autre diminue.
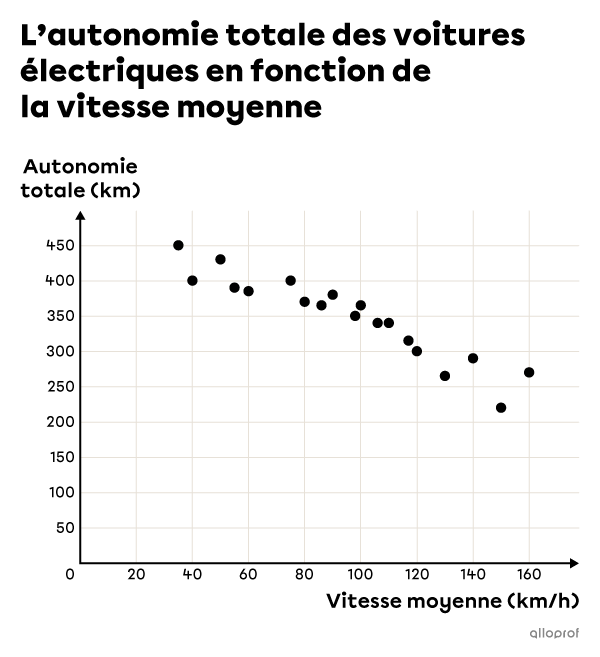
Plus la vitesse moyenne d’une voiture augmente, plus son autonomie totale diminue.
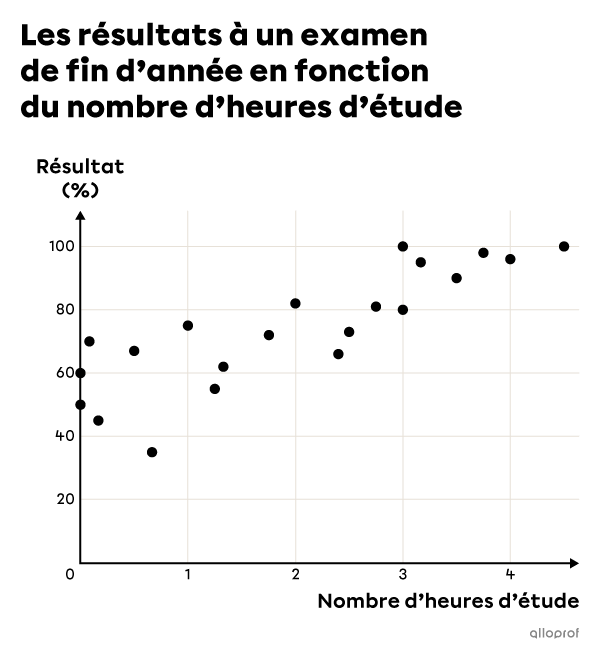
En général, plus le temps consacré à étudier pour un examen augmente, plus le résultat obtenu augmente.
La mesure la plus couramment utilisée pour calculer la force de corrélation est le coefficient de corrélation linéaire, noté |r.| Il s’agit d’une donnée qui peut prendre n’importe quelle valeur entre |-1| et |1.|
-
Une valeur de |r| égale à |1| indique une corrélation positive parfaite.
-
Une valeur de |r| égale à |-1| indique une corrélation négative parfaite.
-
Une valeur de |r| égale à |0| indique qu'il n'y a pas de corrélation entre les 2 variables.
D’ailleurs, quelques méthodes permettent de calculer la valeur de ce coefficient.
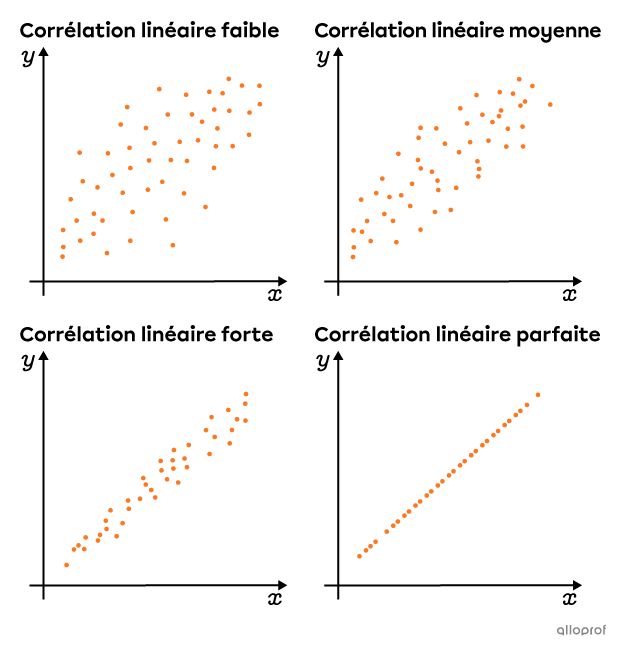
Voici des nuages de points qui montrent une corrélation linéaire positive de plus en plus forte.
Il est important de noter que la corrélation ne permet pas de déterminer la causalité entre 2 variables. Elle ne fait que mesurer l'association entre celles-ci. Ainsi, une forte corrélation entre 2 variables ne signifie pas nécessairement que la variation de l'une est la cause de la variation de l'autre.
Antoine éprouve certaines difficultés à l’école. Pour ses 4 derniers examens d’histoire, il a passé de plus en plus d’heures à étudier. Pourtant, ses notes ont diminué d’une évaluation à l’autre. Il y a donc une corrélation négative observable entre son nombre d’heures d’étude et ses résultats. Est-ce qu’Antoine doit en conclure que son étude lui cause de mauvaises notes et qu’il devrait donc étudier moins?
Réponse : Non! Ses notes qui baissent peuvent être causées par plusieurs autres facteurs. Par exemple, il a peut-être eu un taux d’absentéisme de plus en plus grand. Autrement dit, dernièrement, il a été absent lors de tellement de cours d’histoire qu’il lui manque des informations essentielles pour réussir. Donc, pour Antoine, étudier beaucoup sans avoir vu l’ensemble de la matière à étudier ne l’aidera pas. Il est aussi possible qu’il passe plus d’heures à étudier, mais qu’il soit davantage en contact avec des sources de distractions qu’auparavant. Donc, la durée de son étude, même si elle est plus longue, est moins efficace.
La corrélation entre 2 variables n’est pas toujours linéaire.
La corrélation non linéaire est une forme de corrélation dans laquelle la relation entre les variables ne peut pas être représentée par une droite.
Pour détecter une corrélation non linéaire, il est utile de visualiser les données à l’aide d’un nuage de points. Il faut alors associer la forme du nuage de points au modèle mathématique qui lui ressemble le plus.
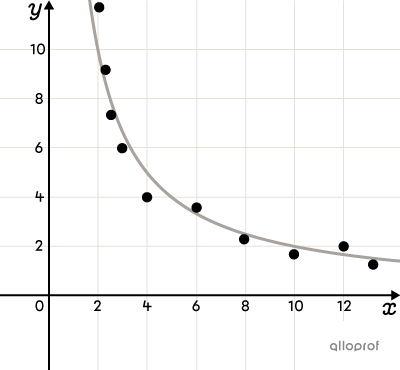
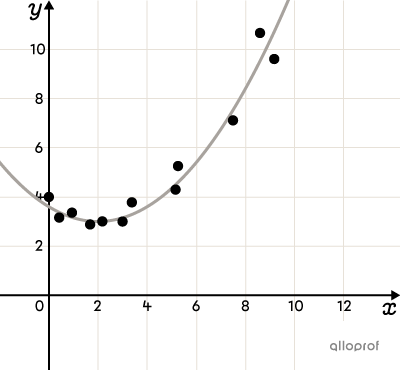
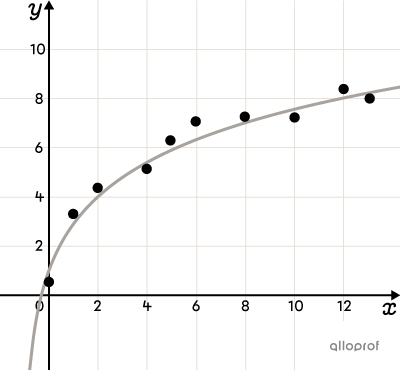
Voici quelques exemples de nuages de points où on peut observer une corrélation non linéaire entre les variables. Il en existe plusieurs autres.