Une des utilités du nuage de points est de pouvoir estimer les résultats à venir. Afin de quantifier la justesse de cette estimation, on calcule le coefficient de corrélation linéaire.
Le coefficient de corrélation linéaire, généralement noté |r|, quantifie la force du lien linéaire entre les deux caractères d’une distribution. Pour le déterminer, on peut procéder par estimation de son allure graphique ou utiliser une formule mathématique.
Le coefficient de corrélation aura toujours une valeur qui se situe dans l'intervalle [-1, 1].
Le coefficient de corrélation linéaire d'une distribution peut donner une idée de l'allure qu'a le nuage de points et inversement. D'abord, le signe du coefficient, positif ou négatif, indique le sens de la pente de la droite de régression. Pour bien comprendre le coefficient de corrélation, voici trois nuages de points qui illustrent bien ces valeurs extrêmes, soit -1, 0 et 1.
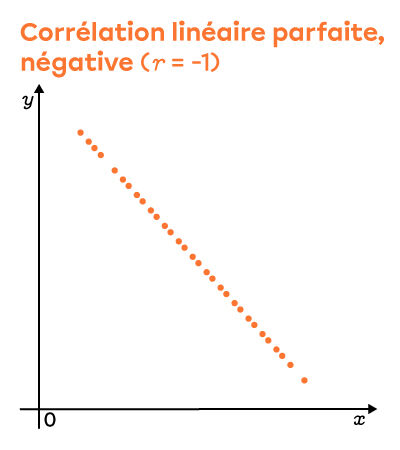
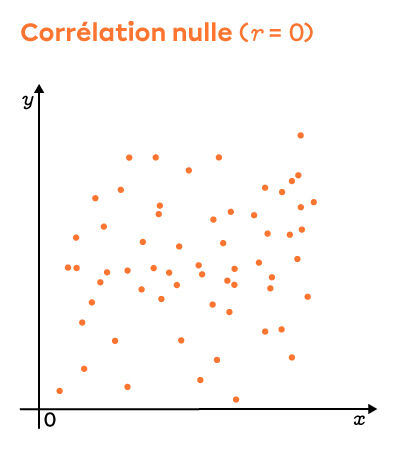
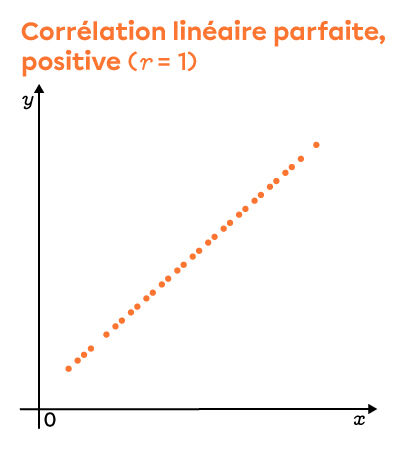
En d'autres mots, plus la valeur du coefficient de corrélation linéaire est près de 1 ou -1, plus le lien linéaire entre les deux variables est fort.
À l'inverse, plus sa valeur est près de 0, plus le lien linéaire entre les deux variables est faible.
Pour calculer les valeurs de |r|, on peut utiliser un graphique ou faire des calculs arithmétiques. Par contre, si on veut seulement les comparer, on peut simplement jeter un coup d'œil aux nuages de points et à l'alignement des points de ceux-ci.
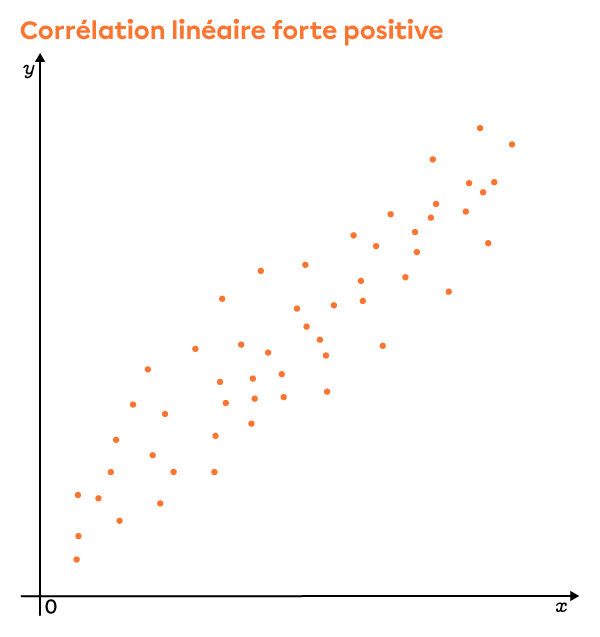
En regardant attentivement ces graphiques, on voit que les points sont plus dispersés dans le deuxième nuage. Ainsi, on peut affirmer que le coefficient de corrélation linéaire est plus faible dans ce nuage que dans le premier.
Afin de bien voir la différence entre chacun des qualificatifs de corrélation, voici des nuages de points qui les représentent.
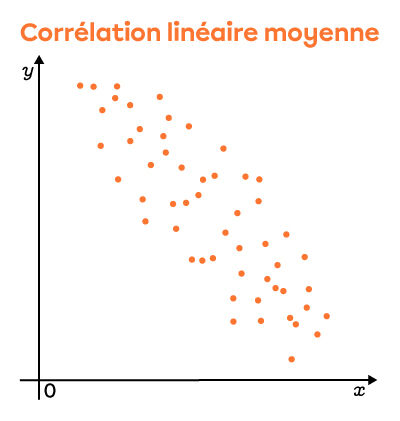
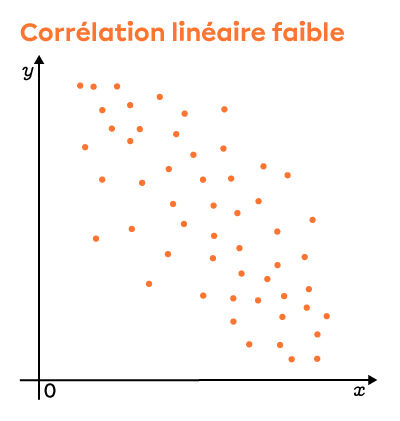
Corrélations linéaires négatives

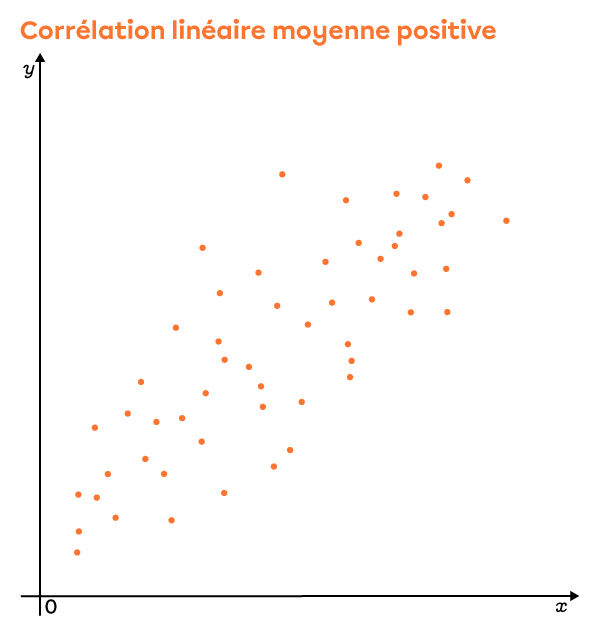
Corrélations linéaires positives
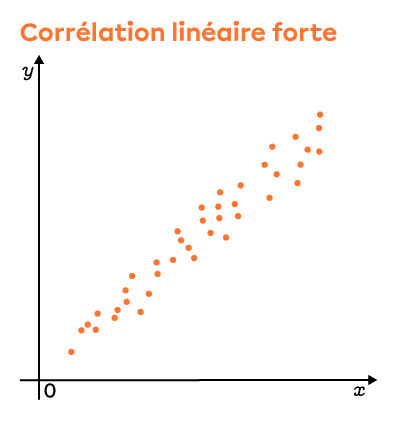
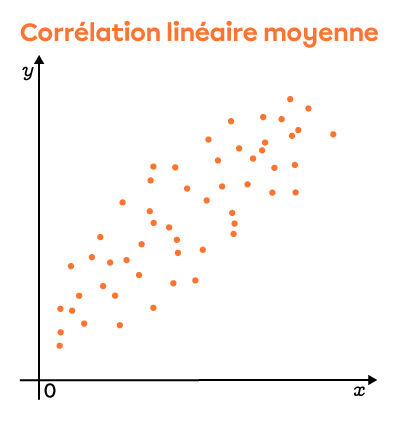
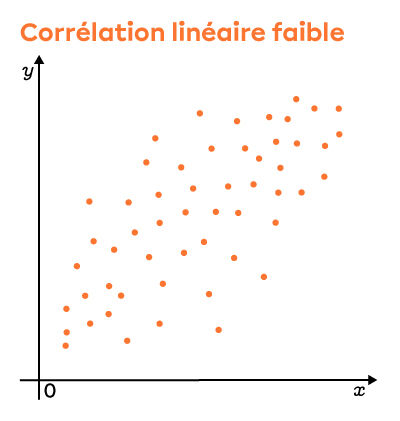
Selon le qualificatif, on voit que le nuage est de plus en plus dispersé. Par contre, il est toujours possible de noter le sens du nuage (positif ou négatif). Lorsque les points sont tellement dispersés qu'il devient impossible d'en déterminer le sens, c'est souvent que le coefficient de corrélation linéaire est nul.
Afin de simplifier la représentation des données amassées, ces dernières sont parfois regroupées en classes et placées dans un tableau à double entrée.
Pour passer d'un nuage de points à un tableau à double entrée, on peut segmenter le nuage afin de bien définir chacune des classes.
Ainsi, ce nuage de points...
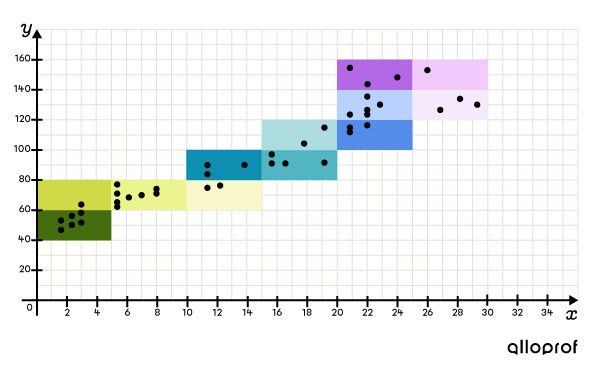
... devient ce tableau à double entrée :
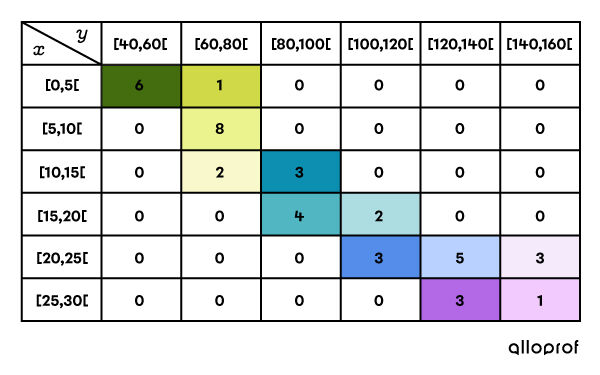
Une fois ce tableau obtenu, il est possible d'estimer la corrélation des données.
Selon le tableau à double entrée précédent, on peut déduire que la corrélation est forte et positive.
Elle est positive, car plus les données augmentent en |X|, plus elles augmentent en |Y|.
Elle est forte, car les données sont regroupées près de la diagonale du tableau à double entrée.
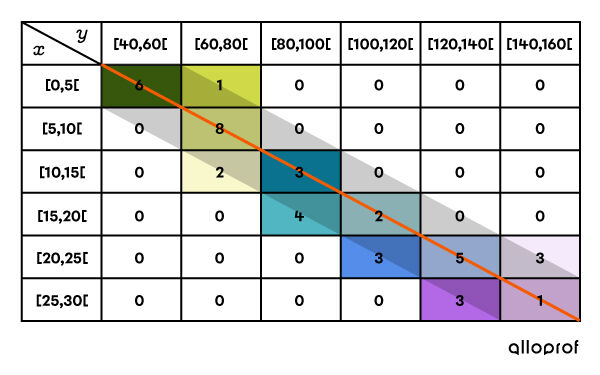
Fait à noter, si les données se situent autour de l'autre diagonale, soit celle qui commence en bas à gauche pour se terminer en haut à droite, la corrélation sera alors négative.
En déterminant de façon plus précise la valeur du coefficient de corrélation linéaire, on peut plus facilement qualifier la corrélation entre deux variables.
||r\approx\pm\left(1-\dfrac{l}{L}\right)||
où
|L :| longueur du rectangle regroupant le nuage de points
|l :| largeur du rectangle regroupant le nuage de points
Pour ce qui est du signe de |r|, il sera déterminé selon le sens du nuage de points.
De façon générale, cette formule permet de trouver une valeur assez représentative du coefficient de corrélation linéaire. Par contre, il existe des outils plus perfectionnés qui calculent intégralement cette valeur.
Généralement, les valeurs suivantes seront utilisées pour qualifier la corrélation linéaire :
| Valeur de |r| | Force du lien linéaire |
|---|---|
|
Près de 0 |
Nulle |
|
Près de |\pm\, 0{,}50| |
Faible |
|
Près de |\pm\, 0{,}75| |
Moyenne |
|
Près de |\pm\, 0{,}87| |
Forte |
|
Près de |\pm\, 1| |
Très forte |
|
|\pm\, 1| |
Parfaite |
Afin d'associer une valeur numérique au coefficient de corrélation, on doit suivre 3 étapes.
-
Tracer le nuage de points.
-
Tracer un rectangle et mesurer sa longueur et sa largeur.
-
Calculer le coefficient de corrélation à l'aide de la formule.
-
Tracer le nuage de points
En plaçant chacun des couples dans un plan cartésien, on obtient le nuage de points suivant.
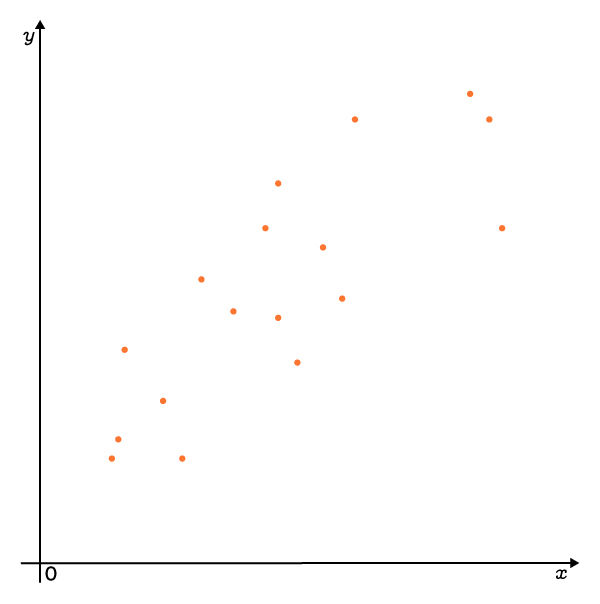
-
Tracer un rectangle et mesurer sa longueur et sa largeur
Le rectangle doit contenir tous les points et être le plus petit possible. Lorsqu'il est tracé, il suffit de prendre une règle graduée et de mesurer les segments.
Puisqu'il n'y a aucune donnée aberrante ou éloignée, on obtient le rectangle suivant.
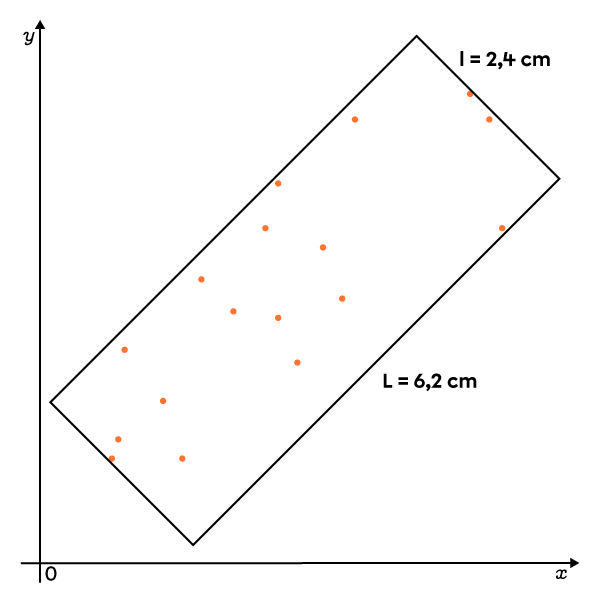
-
Calculer le coefficient de corrélation à l'aide de la formule
|r \approx \pm \left(1 - \dfrac{2{,}4}{6{,}2} \right)|
|r \approx \pm 0{,}61|
|r \approx 0{,}61|, car le nuage de points est de sens positif.
Avec des calculatrices à affichage graphique ou des logiciels comme des tableurs, on peut obtenir un coefficient de corrélation beaucoup plus précis. Il suffit d'entrer l'ensemble des données dans une table de valeurs, de sélectionner la bonne fonction et de laisser le logiciel faire les calculs.
La formule permettant de calculer précisément le coefficient de corrélation linéaire |r| est la suivante. ||r=\dfrac{\sum\left(x-\overline{x}\right)\left(y-\overline{y}\right)}{\sqrt{\sum\left(x-\overline{x}\right)^{2}}\sqrt{\sum\left(y-\overline{y}\right)^{2}}}||
où
|x :| une valeur de la 1re distribution
|\overline{x} :| la moyenne de la 1re distribution
|y :| une valeur de la 2e distribution
|\overline{y} :| la moyenne de la 2e distribution
|\sum :| symbole qui signifie la somme de…