La méthode de la droite médiane-médiane est une méthode permettant de tracer une droite de régression pour un nuage de points donné en utilisant des médianes. Cette droite peut être utilisée pour interpoler ou extrapoler des valeurs, c’est-à-dire pour faire des prédictions.
Voici les étapes à suivre pour trouver la règle de la droite médiane-médiane et pour faire des prédictions à partir d’un ensemble de données à 2 caractères.
-
Ordonner les coordonnées selon la variable indépendante.
-
Séparer la distribution en 3 groupes égaux, si possible.
-
Calculer les points médians de chaque groupe |(M_1, M_2| et |M_3).|
-
Calculer le point moyen |P,| dont les coordonnées sont la moyenne des abscisses et la moyenne des ordonnées des points médians.
-
Déterminer le taux de variation |(a)| de la droite passant par |M_1| et |M_3.|
-
Déterminer l’ordonnée à l’origine |(b)| de la droite passant par |P| et dont le taux de variation est |a.|
-
Prédire des valeurs à l’aide de la règle de la droite.
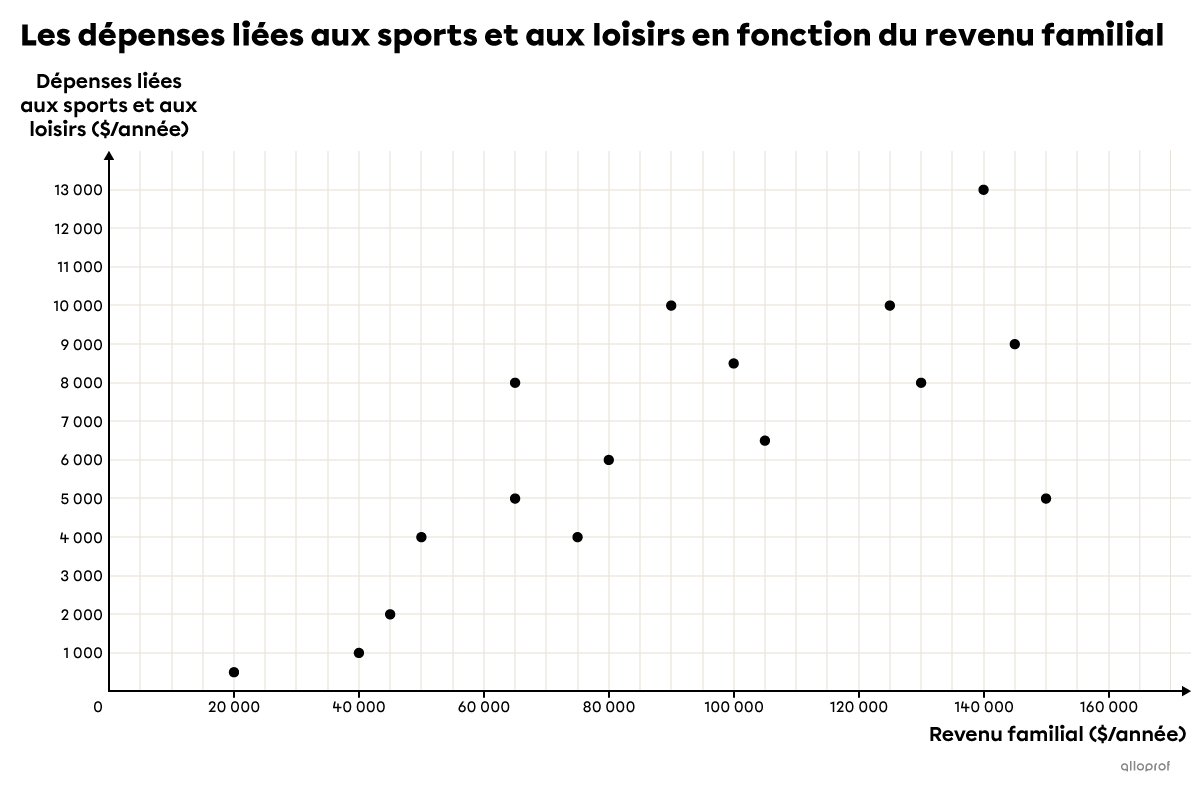
À la suite d’une enquête réalisée auprès de |16| familles québécoises, on s'est intéressé aux dépenses totales liées aux sports et aux loisirs en fonction de leur revenu familial.
La table de valeurs ci-dessous présente les données recueillies. Ces données ont ensuite été placées dans un plan cartésien pour former un nuage de points.
| Revenu familial ($/année) |
|125\ 000| | |65\ 000| | |35\ 000| | |145\ 000| | |130\ 000| | |80\ 000| | |50\ 000| | |40\ 000| |
|---|---|---|---|---|---|---|---|---|
| Dépenses liées aux sports et aux loisirs ($/année) |
|10\ 000| | |8\ 000| | |1\ 000| | |9\ 000| | |8\ 000| | |6\ 000| | |4\ 000| | |2\ 000| |
| Revenu familial ($/année) |
|90\ 000| | |20\ 000| | |75\ 000| | |105\ 000| | |100\ 000| | |140\ 000| | |150\ 000| | |65\ 000| |
| Dépenses liées aux sports et aux loisirs ($/année) |
|10\ 000| | |500| | |4\ 000| | |6\ 000| | |8\ 000| | |13\ 000| | |5\ 000| | |5\ 000| |
a) Une famille a un revenu familial annuel de |250\ 000\ \$.| Si cette famille suit la même tendance que les autres familles québécoises interrogées, à quel montant son budget consacré aux sports et aux loisirs s'élève-t-il?
b) Une famille dépense en moyenne |7\ 500\ \$| par année pour les sports et les loisirs. À combien son revenu familial annuel s’élève-t-il si elle suit les habitudes d’une famille québécoise typique?
-
Ordonner les coordonnées selon la variable indépendante
| Revenu familial ($/année) |
|20\ 000| | |35\ 000| | |40\ 000| | |50\ 000| | |65\ 000| | |65\ 000| | |75\ 000| | |80\ 000| |
|---|---|---|---|---|---|---|---|---|
| Dépenses liées aux sports et aux loisirs ($/année) |
|500| | |1\ 000| | |2\ 000| | |4\ 000| | |5\ 000| | |8\ 000| | |4\ 000| | |6\ 000| |
| Revenu familial ($/année) |
|90\ 000| | |100\ 000| | |105\ 000| | |125\ 000| | |130\ 000| | |140\ 000| | |145\ 000| | |150\ 000| |
| Dépenses liées aux sports et aux loisirs ($/année) |
|10\ 000| | |8\ 000| | |6\ 000| | |10\ 000| | |8\ 000| | |13\ 000| | |9\ 000| | |5\ 000| |
-
Séparer la distribution en 3 groupes égaux, si possible
Puisque le nombre de données |(16)| n'est pas divisible par |3,| il faut séparer les groupes de sorte que les 1er et 3e groupes aient le même nombre de données. Les 1er et 3e groupes ont donc |5| couples de données chacun et le 2e en a |6.|
| Revenu familial ($/année) |
|20\ 000| | |35\ 000| | |40\ 000| | |50\ 000| | |65\ 000| | |
|---|---|---|---|---|---|---|
| Dépenses liées aux sports et aux loisirs ($/année) |
|500| | |1\ 000| | |2\ 000| | |4\ 000| | |5\ 000| | |
| Revenu familial ($/année) |
|65\ 000| | |75\ 000| | |80\ 000| | |90\ 000| | |100\ 000| | |105\ 000| |
| Dépenses liées aux sports et aux loisirs ($/année) |
|8\ 000| | |4\ 000| | |6\ 000| | |10\ 000| | |8\ 000| | |6\ 000| |
| Revenu familial ($/année) |
|125\ 000| | |130\ 000| | |140\ 000| | |145\ 000| | |150\ 000| | |
| Dépenses liées aux sports et aux loisirs ($/année) |
|10\ 000| | |8\ 000| | |13\ 000| | |9\ 000| | |5\ 000| |
-
Calculer les points médians de chaque groupe |\boldsymbol{(M_1, M_2}| et |\boldsymbol{M_3)}|
Il suffit de trouver la médiane en |x| et en |y| de chacun des groupes afin de former 3 points.
Attention! Pour ce qui est des |y,| il ne faut pas nécessairement prendre celui qui est lié au |x| médian. Il faut bien choisir la valeur médiane des |y.|
| Médiane des abscisses |\boldsymbol{(x)}| | Médiane des ordonnées |\boldsymbol{(y)}| | Point médian | |
|---|---|---|---|
| 1er groupe | |x_1=40\ 000| | |y_1=2\ 000| | |M_1(40\ 000,2\ 000)| |
| 2e groupe | |\begin{align}x_2&=\dfrac{80\ 000+90\ 000}{2}\\&=85\ 000\end{align}| | |\begin{align}y_2&=\dfrac{6\ 000+8\ 000}{2}\\&=7\ 000\end{align}| | |M_2(85\ 000,7\ 000)| |
| 3e groupe | |x_3=140\ 000| | |y_3=9\ 000| | |M_3(140\ 000,9\ 000)| |
-
Calculer le point moyen |\boldsymbol{P},| dont les coordonnées sont la moyenne des abscisses et la moyenne des ordonnées des points |\boldsymbol{M_1, M_2}| et |\boldsymbol{M_3}|
||\begin{align}&P\left(\dfrac{x_1+x_2+x_3}{3},\dfrac{y_1+y_2+y_3}{3}\right)\\ &P\left(\dfrac{40\ 000+85\ 000+140\ 000}{3},\dfrac{2\ 000+7\ 000+9\ 000}{3}\right)\\ &P\ \left(88\ 333{,}\overline{3};6\ 000\right)\end{align}||
-
Déterminer le taux de variation |\boldsymbol{(a)}| de la droite passant par |\boldsymbol{M_1}| et |\boldsymbol{M_3}| ||\begin{align}a&=\dfrac{y_3-y_1}{x_3-x_1}\\&=\dfrac{9\ 000-2\ 000}{140\ 000-40\ 000}\\&=0{,}07\end{align}||
-
Déterminer l’ordonnée à l’origine |\boldsymbol{(b)}| de la droite passant par |\boldsymbol{P}| et dont le taux de variation est |\boldsymbol{a}| ||\begin{align}y&=ax+b\\ y&=0{,}07x+b\\ 6\ 000&=0{,}07(88\ 333{,}\overline{3})+b\\6\ 000&\approx 6\ 183+b\\-183&\approx b\end{align}||
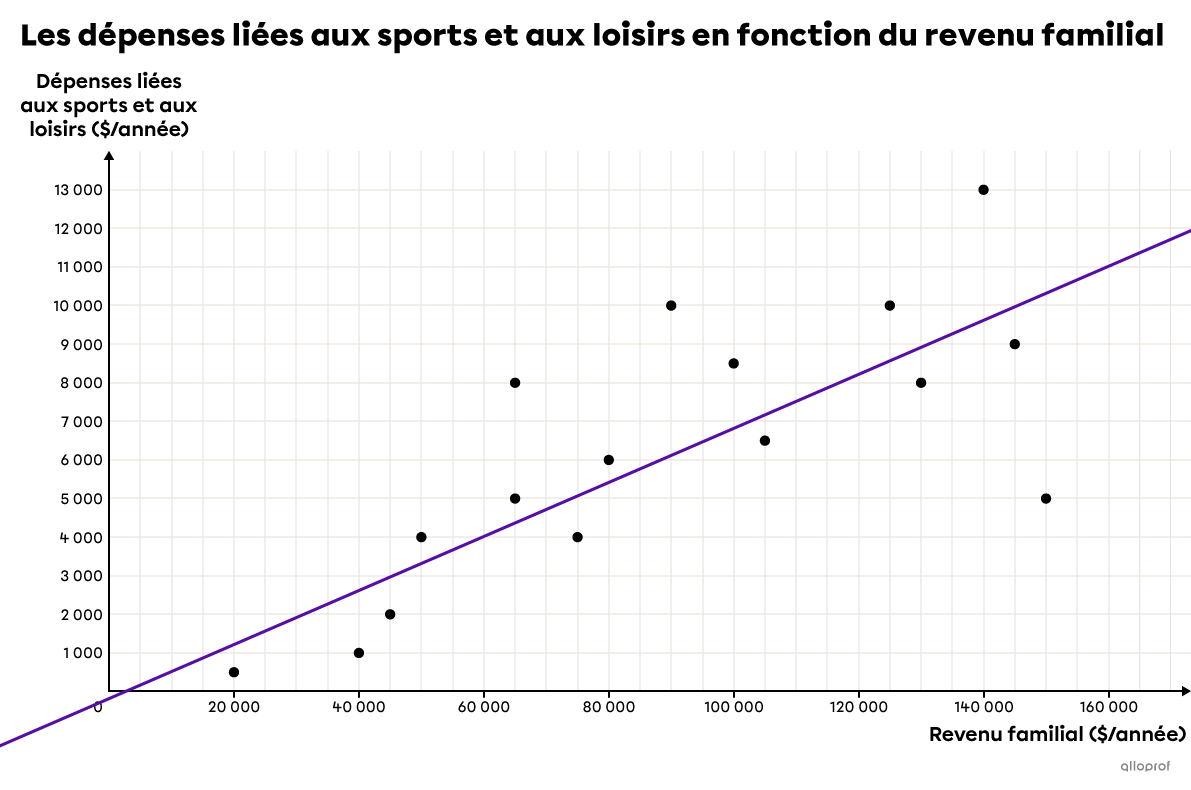
Ainsi, la règle de la droite médiane-médiane est |y=0{,}07x-183,| où |x| est le revenu familial et |y,| le budget consacré aux sports et aux loisirs, tous les 2 en |\$| par année. On peut tracer cette droite dans le graphique.
-
Prédire des valeurs à l’aide de la règle de la droite
a) Une famille a un revenu familial annuel de |\boldsymbol{250\ 000\ \$.}| Si cette famille suit la même tendance que les autres familles québécoises interrogées, à quel montant son budget consacré aux sports et aux loisirs s'élève-t-il?
On peut faire une estimation des dépenses de cette famille en sports et en loisirs à l’aide de la droite de régression. Il s’agit d’une extrapolation, car le revenu familial en question |(250\ 000\ \$)| est en dehors de l’intervalle étudié |(20\ 000| à |150\ 000\ \$).|
On remplace la variable |x| par |250\ 000| dans la règle de la droite de régression et on complète le calcul. ||\begin{align}y&=0{,}07x-183\\y&=0{,}07(250\ 000)-183\\y&=17\ 500-183\\y&=17\ 317\ \$ \end{align}||
Réponse : Si une famille ayant un revenu annuel de |250\ 000\ \$| suit la même tendance que les autres familles québécoises interrogées, elle devrait consacrer environ |17\ 317\ \$| aux sports et aux loisirs.
b) Une famille dépense en moyenne |\boldsymbol{7\ 500\ \$}| par année pour les sports et les loisirs. À combien son revenu familial annuel s’élève-t-il si elle suit les habitudes d’une famille québécoise typique?
On peut estimer le revenu annuel de cette famille à l’aide de la droite de régression. Il s’agit d’une interpolation, car le budget annuel consacré aux loisirs et aux sports |(7\ 500\ \$)| est à l’intérieur de l’intervalle étudié |(500| à |13\ 000\ \$).|
On remplace |y| par |7\ 500| et on isole |x.| ||\begin{align} y &= 0{,}07x-183 \\ 7\ 500 &= 0{,}07x-183 \\ 7\ 500\boldsymbol{\color{#ec0000}{+183}} &= 0{,}07x-183\boldsymbol{\color{#ec0000}{+183}} \\ \dfrac{7\ 683}{\boldsymbol{\color{#ec0000}{0{,}07}}} &= \dfrac{0{,}07x}{\boldsymbol{\color{#ec0000}{0{,}07}}} \\ 109\ 757\ \$ &\approx x \end{align}||
Réponse : Si une famille dépense en moyenne |7\ 500\ \$| par année pour les sports et les loisirs, on peut s’attendre à ce que son revenu familial annuel soit d’environ |109\ 757\ \$.|
Remarque : Le même problème a été résolu dans les fiches portant sur la droite de régression et sur la droite de Mayer. Chaque fois, on obtient des résultats comparables.
Lorsqu’il faut ordonner les points
-
On ordonne les points selon leur abscisse. Il ne faut pas ordonner les abscisses et les ordonnées séparément.
-
Si 2 points ont la même abscisse, mais des ordonnées différentes, alors celui avec la plus petite ordonnée est placé en premier.
Exemple :
Voici une table de valeurs.
| |x| | |13| | |12| | |13| | |13| | |10| | |12| |
|---|---|---|---|---|---|---|
| |y| | |35| | |24| | |35| | |28| | |25| | |29| |
On obtient la table suivante.
| |x| | |10| | |12| | |12| | |13| | |13| | |13| |
|---|---|---|---|---|---|---|
| |y| | |25| | |24| | |29| | |28| | |35| | |35| |
On n’obtient pas celle-ci.
| |x| | |10| | |12| | |12| | |13| | |13| | |13| |
|---|---|---|---|---|---|---|
| |y| | |24| | |25| | |28| | |29| | |35| | |35| |
Lorsqu’il faut séparer les points en 3 groupes
-
Si le nombre de points se divise par 3, les groupes sont égaux.
Par exemple, |18 = 6 + 6 + 6.| -
Si le nombre de points ne se divise pas par 3, il faut s’assurer que le 1er et le 3e groupe soient de la même taille et que la taille des 3 groupes soit le plus égal possible. Voici 2 exemples.
-
|29 = 10 + 9 + 10| et non |9 + 11 + 9|
-
|25 = 8 + 9 + 8| et non |9 + 7 + 9|
-
Lorsqu’il faut calculer les points médians
-
Comme les points sont déjà placés en ordre selon les |x,| il suffit de sélectionner la médiane en |x| de chaque groupe.
-
Pour ce qui est des valeurs de |y,| il ne faut pas nécessairement prendre celle qui forme un couple avec le |x| choisi. Il faut bien choisir la médiane en |y| de chaque groupe.
Exemple :
| 1er groupe | 2e groupe | 3e groupe | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| |x| | |1| | |\boldsymbol{2}| | |4| | |4| | |\boldsymbol{5}| | |\boldsymbol{6}| | |7| | |7| | |\boldsymbol{8}| | |10| |
| |y| | |5| | |8| | |\boldsymbol{7}| | |9| | |\boldsymbol{10}| | |\boldsymbol{10}| | |13| | |\boldsymbol{16}| | |14| | |20| |
-
Dans le 1er groupe, il y a un nombre impair de points. L’abscisse médiane est |2.| Comme les ordonnées de ce groupe sont |5,| |7| et |8,| l’ordonnée médiane de ce groupe est |\boldsymbol{7}| et non |8.| Ainsi, le point |M_1| a comme coordonnées |(2,7)| même si le point |(2,7)| ne fait pas partie du nuage de points.
-
Dans le 2e groupe, il y a un nombre pair de données.||\begin{align} x_2 &= \dfrac{5+6}{2}=5{,}5 \\ y_2 &=\dfrac{10+10}{2}=10 \end{align}||Ainsi, le point |M_2| est |(5{,}5; 10).|
-
Dans le 3e groupe, |x_3=8| et |y_3=\boldsymbol{16}| et non |14.| Ainsi, le point |M_3| est |(8, 16).|
Une erreur s’est glissée dans cette vidéo.
À 7 min 30 s, on devrait lire : les points |M1 (45,54)| et |M3 (92,84).| Le calcul est exact, mais il y a une erreur dans la 1re phrase.
La méthode de la droite médiane-médiane prend généralement un peu plus de temps à effectuer que celle de la droite de Mayer, mais ça ne veut pas dire que c’est une moins bonne méthode. Voici un exemple où on présente les 2 démarches en parallèle dans le but de les comparer.
Lors d’une saison de hockey, les points marqués par tous les joueurs sont comptabilisés. Les points d’un joueur comprennent les passes décisives (assist en anglais) et les buts. Au hockey, on compte jusqu’à 2 passes décisives par but marqué, soit les 2 dernières passes effectuées juste avant le but.
Voici le nombre de passes décisives et de points de 10 attaquants réguliers des Bruins de Boston lors de la saison 2022-2023 de la LNH.
| Joueur | Nombre de passes | Nombre de points |
|---|---|---|
| D. Pastrnak | ||49|| | ||109|| |
| B. Marchand | ||46|| | ||66|| |
| P. Zacha | ||37|| | ||58|| |
| P. Bergeron | ||30|| | ||57|| |
| D. Krejci | ||40|| | ||56|| |
| J. DeBrusk | ||23|| | ||48|| |
| C. Coyle | ||29|| | ||44|| |
| T. Hall | ||20|| | ||36|| |
| T. Frederic | ||14|| | ||30|| |
| N. Foligno | ||16|| | ||28|| |
Si on se fie aux données de cette équipe, un joueur qui aurait fait |60| passes décisives aurait dû terminer la saison avec combien de points?
-
Ordonner les coordonnées selon la variable indépendante
| Nombre de passes | |14| | |16| | |20| | |23| | |29| | |30| | |37| | |40| | |46| | |49| |
|---|---|---|---|---|---|---|---|---|---|---|
| Nombre de points | |30| | |28| | |36| | |48| | |44| | |57| | |58| | |56| | |66| | |109| |
La droite médiane-médiane
-
Séparer la distribution en 3 groupes égaux
Les 1er et 3e groupes ont |3| couples de données chacun et le 2e en a |4.|
-
Calculer les points médians de chaque groupe |\boldsymbol{(M_1, M_2}| et |\boldsymbol{M_3)}|
| Médiane des abscisses |(x)| | Médiane des ordonnées |(y)| | Point médian | |
| 1er groupe | |x_1=16| | |y_1=30| | |M_1(16,30)| |
| 2e groupe | |\begin{align}x_2&=\dfrac{29+30}{2}\\&=29{,}5\end{align}| | |\begin{align}y_2&=\dfrac{48+57}{2}\\&=52{,}5\end{align}| | |M_2(29{,}5;52{,}5)| |
| 3e groupe | |x_3=46| | |y_3=66| | |M_3(46,66)| |
-
Calculer le point moyen |\boldsymbol{P},| dont les coordonnées sont la moyenne des abscisses et la moyenne des ordonnées des points |\boldsymbol{M_1, M_2}| et |\boldsymbol{M_3}|
||\begin{align}P&\left(\dfrac{16+29{,}5+46}{3},\dfrac{30+52{,}5+66}{3}\right)\\ P&\ (\ 30{,}5;\ 49{,}5\ )\end{align}||
-
Déterminer le taux de variation |\boldsymbol{(a)}| de la droite passant par |\boldsymbol{M_1}| et |\boldsymbol{M_3}| ||\begin{align}a&=\dfrac{y_3-y_1}{x_3-x_1}\\&=\dfrac{66-30}{46-16}\\&=1{,}2\end{align}||
-
Déterminer l’ordonnée à l’origine |\boldsymbol{(b)}| de la droite passant par |\boldsymbol{P}| et dont le taux de variation est |\boldsymbol{a}| ||\begin{align} y &= ax+b \\ y &= 1{,}2x+b \\ 49{,}5 &= 1{,}2(30{,}5)+b \\ 49{,}5 &= 36{,}6+b \\ 12{,}9 &= b \end{align}||Ainsi, la règle de la droite médiane-médiane est |\color{#560fa5}{y=1{,}2x+12{,}9},| où |x| est le nombre de passes décisives et |y,| le nombre de points.
-
Prédire des valeurs à l’aide de la règle de la droite
On fait une extrapolation du nombre de points à l’aide de la droite médiane-médiane en remplaçant la variable |x| par |60.| ||\begin{align} y &= 1{,}2x+12{,}9 \\&= 1{,}2(60)+12{,}9 \\ &= 72+12{,}9 \\ &= 84{,}9\\ &\approx 85\ \text{points} \end{align}||
La droite de Mayer
-
Séparer la distribution en 2 groupes égaux
Les |5| couples dont le nombre de passes est de |29| et moins constituent le 1er groupe. Les |5| autres couples forment le 2e groupe.
-
Calculer les points moyens de chaque groupe |\boldsymbol{(P_1}| et |\boldsymbol{P_2)}|
| Moyenne des abscisses |(\overline{x})| | Moyenne des ordonnées |(\overline{y})| | Point moyen | |
| 1er groupe | |\begin{align}\overline{x}_1 &= \dfrac{14+16+20+23+29}{5} \\ &=20{,}4\end{align}| | |\begin{align}\overline{y}_1 &= \dfrac{30+28+36+48+44}{5} \\ &=37{,}2\end{align}| | |P_1(20{,}4; 37{,}2)| |
| 2e groupe | |\begin{align}\overline{x}_2 &= \dfrac{30+37+40+46+49}{5} \\ &=40{,}4\end{align}| | |\begin{align}\overline{y}_2 &= \dfrac{57+58+56+66+109}{5} \\ &=69{,}2\end{align}| | |P_2(40{,}4;69{,}2)| |
-
Trouver la règle de la droite de régression passant par les points |\boldsymbol{P_1}| et |\boldsymbol{P_2}|
Comme il s’agit d’une droite, la règle est de la forme |y=ax+b.| On commence par calculer la pente |(a).| ||\begin{align}a&=\dfrac{\overline{y}_2-\overline{y}_1}{\overline{x}_2-\overline{x}_1}\\&=\dfrac{69{,}2-37{,}2}{40{,}4-20{,}4}\\&= 1{,}6\end{align}||Ensuite, on remplace |a| par |1{,}6| et les variables |x| et |y| par les coordonnées d’un des 2 points, puis on isole |b.| ||\begin{align} y &= ax+b \\ y &= 1{,}6x+b \\ 37{,}2 &= 1{,}6(20{,}4)+b \\ 37{,}2 &= 32{,}64+b \\ 4{,}56 &= b \end{align}||Ainsi, la règle de la droite de régression trouvée à l’aide de la méthode de la droite de Mayer est |\color{#3b87cd}{y=1{,}6x+4{,}56},| où |x| est le nombre de passes décisives et |y,| le nombre de points.
-
Prédire des valeurs à l’aide de la règle de la droite
Il s’agit d’une extrapolation, car le nombre de passes |(60)| est à l’extérieur de l’intervalle étudié |(14| à |49).| On estime donc le nombre de points à l’aide de la droite de Mayer en remplaçant |x| par |60.| ||\begin{align} y &= 1{,}6x+4{,}56 \\&= 1{,}6(60)+4{,}56 \\ &= 96+4{,}56\\&= 100{,}56\\ &\approx 101\ \text{points} \end{align}||
Réponse : Un joueur qui fait |60| passes décisives dans une saison devrait obtenir environ |85| points selon la droite de médiane-médiane ou |101| points selon la droite de Mayer.
La méthode médiane-médiane se base sur le calcul de la médiane, alors que celle de Mayer se base sur le calcul de la moyenne. Or, la moyenne, contrairement à la médiane, est une mesure de tendance centrale qui est très influencée par les données éloignées, aussi appelées données aberrantes. Ainsi, les données aberrantes n'affectent pas la droite médiane-médiane. C’est donc la méthode à privilégier lorsqu’il y en a dans une distribution.
Si on revient sur l’exemple précédent et qu’on trace le nuage de points et les 2 droites dans le même graphique, il est en effet possible de constater que la droite médiane-médiane est moins influencée par la donnée aberrante que celle de Mayer.
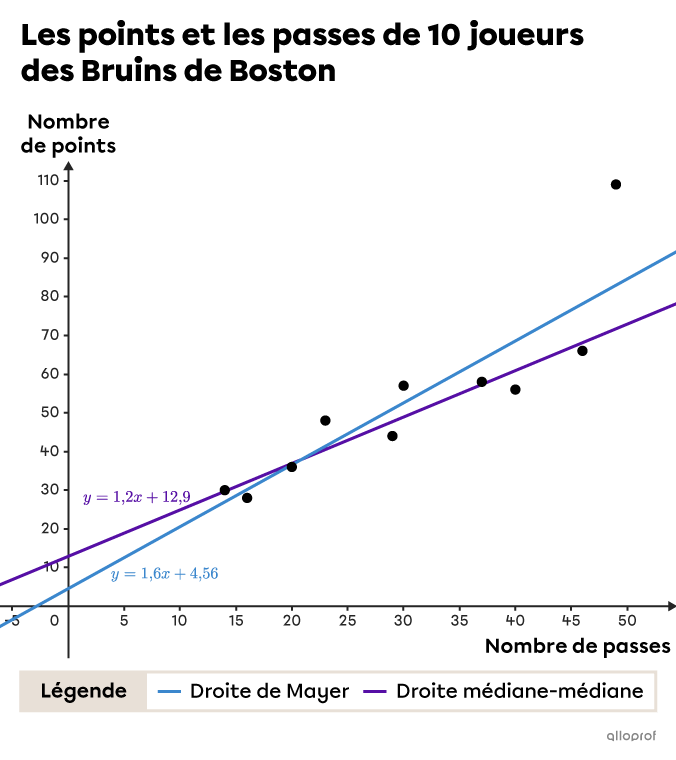
D’abord, on remarque que la pente des 2 droites est assez différente. Pour la droite médiane-médiane, le taux de variation est de |1{,}2,| alors que la droite de Mayer a une pente de |1{,}6.|
On remarque aussi que le point |(49,109),| qui représente les données de David Pastrnak, est éloigné des autres. Ce joueur a accumulé beaucoup plus de points au total par rapport à son nombre de passes décisives que le reste de son équipe |\left(\dfrac{109}{49} \approx 2{,}22\right).|
Les données de Pastrnak ont eu une influence sur la méthode de Mayer, car elles ont été incluses dans les calculs des points moyens. Cela a eu pour effet d’augmenter la valeur de la pente de la droite de Mayer par rapport à l’autre méthode. En effet, le point |(49,109),| même s’il est élevé, n’influence pas les points médians. C’est pourquoi la droite médiane-médiane est moins inclinée et s’ajuste mieux à l’ensemble des données, ce qu’on peut observer sur le graphique. Au contraire, la droite de Mayer est plus inclinée pour se rapprocher du point |(49,109).| Elle est donc moins ajustée au reste du nuage de points.
Conclusion : On considère donc que les prédictions faites à partir de la droite médiane-médiane sont plus représentatives de l’ensemble des joueurs. Ainsi, un joueur qui fait |60| passes décisives dans une saison devrait obtenir environ |85| points et non |101.|