Une étude statistique sert à recueillir des données. Lorsque ces données forment une distribution à 2 caractères, il est possible de les représenter dans un tableau à double entrée ou dans un plan cartésien. La représentation des données dans un graphique se nomme un nuage de points, aussi appelé un diagramme de dispersion.
Un nuage de points est un graphique qui représente chaque couple d'une distribution à 2 variables quantitatives.
S'il existe un lien de dépendance entre les caractères étudiés, on place la variable indépendante sur l’axe des abscisses |(x)| et la variable dépendante sur l’axe des ordonnées |(y).|
Le nuage de points sert à représenter visuellement les différentes réponses obtenues lors d’une enquête statistique. Ainsi, il ne faut pas relier les points dans le but de former une droite ou une courbe quelconque. Par contre, il est parfois possible d'associer un nuage de points à un modèle mathématique (linéaire, exponentiel, polynomial, etc.). C’est ce qu’on appelle faire de la modélisation. En effet, le nuage de points peut sembler former une ligne droite ou une courbe pouvant être associée à une fonction connue.
D’abord, voici comment on peut construire un nuage de points.
Dans une école, on a fait une enquête pour connaitre les habitudes de jeux vidéos des jeunes. Pour un jeu en particulier, on s'est intéressé au temps nécessaire pour compléter une partie ainsi qu'au nombre de parties jouées. Voici un tableau qui présente les réponses amassées.
| Durée d'une partie (min) |
Nombre de parties jouées | Durée d'une partie (min) |
Nombre de parties jouées | Durée d'une partie (min) |
Nombre de parties jouées |
|---|---|---|---|---|---|
| |12| | |2| | |8| | |3| | |12| | |2| |
| |7| | |5| | |11| | |4| | |7| | |6| |
| |10| | |3| | |10| | |3| | |9| | |4| |
| |12| | |3| | |8| | |4| | |11| | |3| |
| |9| | |3| | |9| | |3| | |7| | |8| |
| |8| | |3| | |12| | |1| | |9| | |4| |
À l'aide de ces données, trace le nuage de points associé à cette enquête.
-
Faire la liste des couples de données (les coordonnées) du nuage
Dans cet exemple, il faut placer un point à chacune des coordonnées suivantes.
|(12, 2),| |(7, 5),| |(10, 3),| |(12, 3),| |(9, 3),| |(8, 3),| |(11, 4),| |(8, 4),| |(12, 1),| |(7, 6),| |(9, 4),| |(11, 3),| |(7, 8)|
En fait, chacune de ces coordonnées représente une réponse donnée par un des individus de l'échantillon ou de la population.
-
Tracer ces points dans un plan cartésien
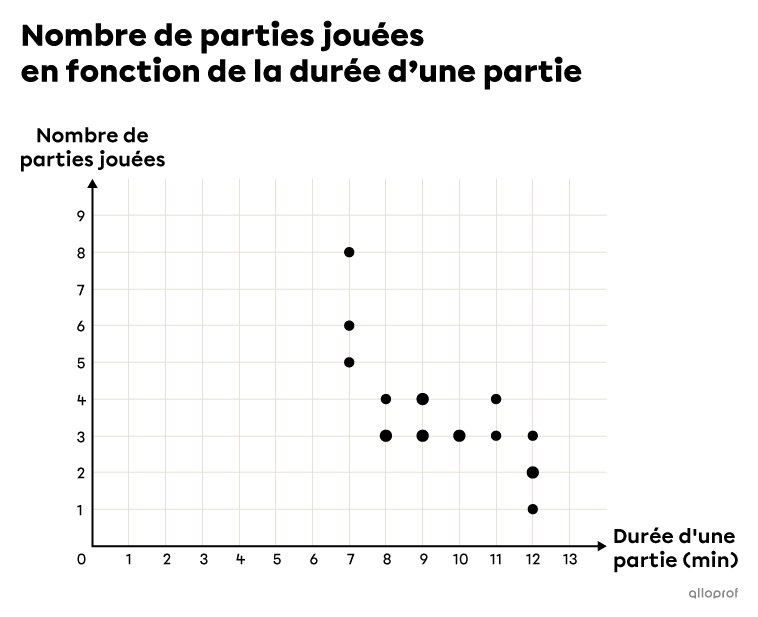
Remarque : Le nuage de points peut être un peu trompeur, puisque si un même couple de données revient à plusieurs reprises, il n’y a tout de même qu’un seul point qui apparait dans le graphique. Dans l'exemple précédent, le couple |(9,4)| revient à 2 reprises, mais on ne peut voir qu'un seul point qui a pour coordonnées |(9,4).| Il est possible de grossir un point pour indiquer qu'il se répète, mais cela ne permet pas de savoir combien de fois il se répète. D’ailleurs, cette façon de faire n’est pas observée partout.
Dans l’exemple précédent, on peut observer une tendance dans le nuage de points. En effet, on remarque que plus le temps pour une partie augmente, plus le nombre de parties jouées diminue. On dit alors qu’il y a une corrélation entre les 2 variables. On peut calculer la force de cette corrélation à l’aide du coefficient de corrélation. On peut aussi modéliser cette situation à l’aide d’une droite de régression ou à l’aide d’une courbe. Le but est de trouver le modèle qui s’ajuste le mieux au nuage de points.
Un nuage de points tiré d’une situation réelle montre rarement des points parfaitement alignés ou des points qui forment une courbe parfaite. Néanmoins, il est souvent possible d’associer le nuage de points en question à un modèle mathématique, c’est-à-dire à une fonction qui est bien connue et avec laquelle on peut travailler.
Un modèle mathématique est une représentation d’un phénomène complexe à l’aide des outils mathématiques connus (fonctions, règles, graphiques, etc.)
La modélisation est l’action de décrire des données réelles observées à l’aide d’un modèle mathématique dans le but d’analyser ces données plus facilement et de faire des prédictions.
Une courbe de tendance est une courbe qui modélise un nuage de points donné. Il s’agit de la courbe qui s’ajuste le mieux à la majorité des points.
Une droite de régression est le nom donné à une courbe de tendance lorsqu’il s’agit d’une ligne droite.
Plusieurs fonctions servent de modèles mathématiques pour différents nuage de points.
Les scientifiques, les chercheurs et les statisticiens ont comme préoccupation de trouver le modèle mathématique le plus approprié pour les données qu’ils ou elles ont recueillies. Cependant, il suffit généralement d’associer les nuages de points à des fonctions linéaires (des droites) ou à des fonctions rationnelles.
Voici la plupart des fonctions possibles. Chaque fonction est classée selon qu’elle forme une droite, une courbe ou un autre modèle.
Lorsqu’un nuage de points présente une tendance linéaire, c’est-à-dire que les points semblent former une ligne droite, on peut le modéliser à l’aide d’une des fonctions suivantes.
La fonction polynomiale de degré 0
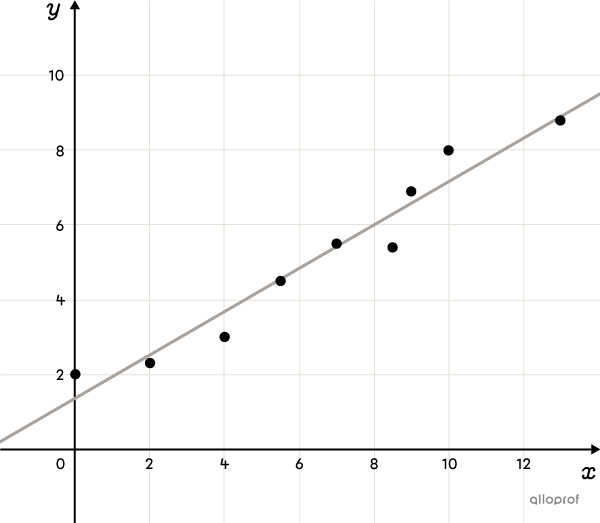
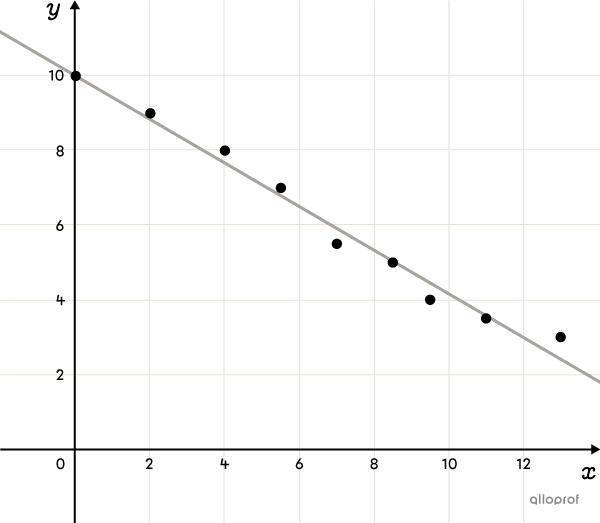
La droite qui s’ajuste le mieux à un nuage de points est la droite de régression. Plusieurs méthodes existent pour déterminer sa règle, notamment la méthode de la droite de Mayer et celle de la droite médiane-médiane.
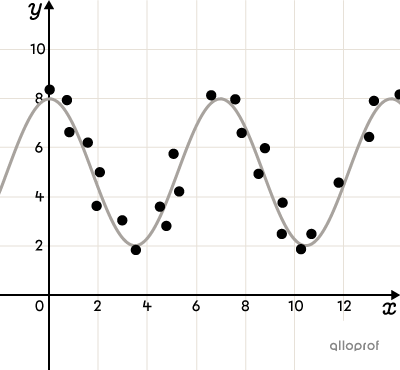
Voici quelques-unes des fonctions qui peuvent servir de modèles mathématiques pour des nuages de points qui ont l’allure d’une courbe. Pour déterminer le modèle le plus approprié, on peut parfois se fier au contexte. Par exemple, le nombre de bactéries dans un échantillon en fonction du temps suit généralement une croissance exponentielle. C’est donc le modèle qu’il faudrait choisir. Dans d’autres situations, il est tout à fait possible de modéliser les données à l’aide de 2 fonctions différentes et d’obtenir des prédictions fiables dans les 2 cas.
La fonction rationnelle

La fonction polynomiale de degré 2 (notion avancée)
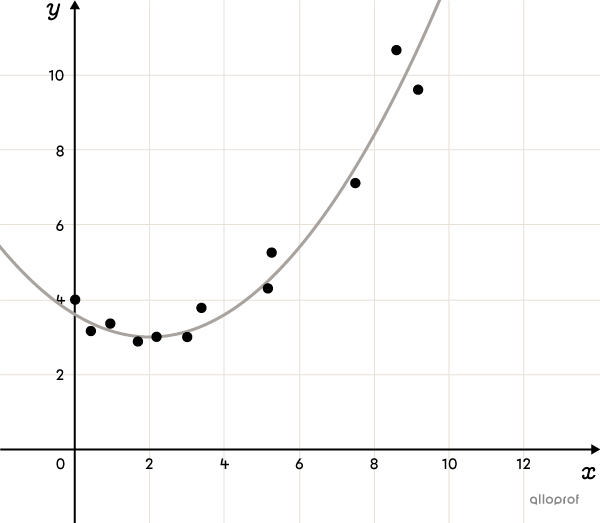
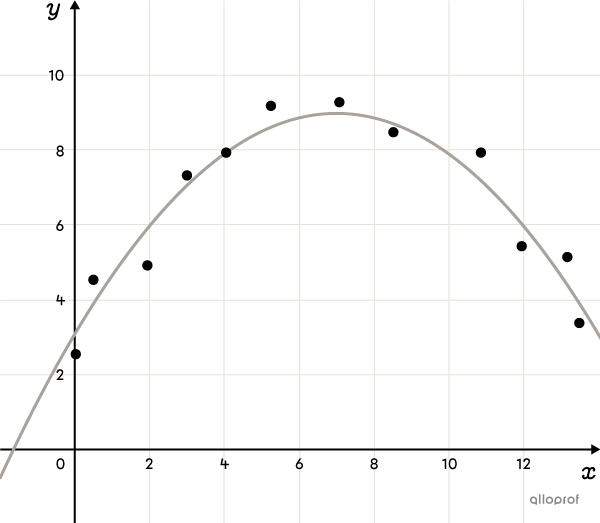
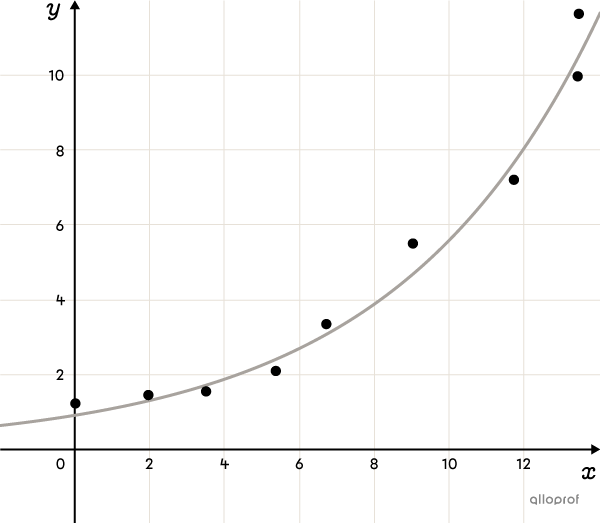
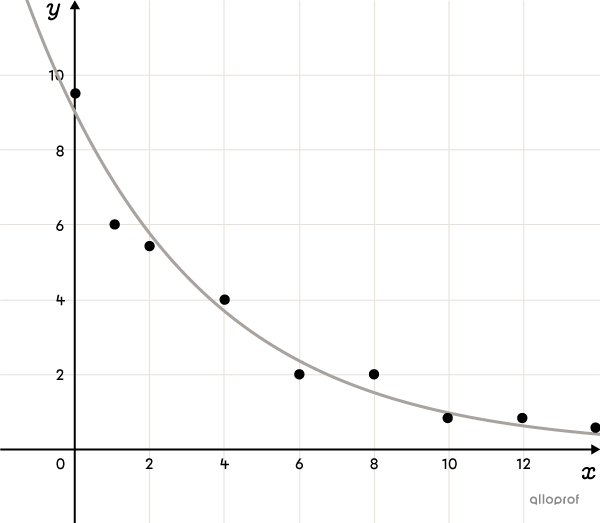
La fonction exponentielle (notion avancée)
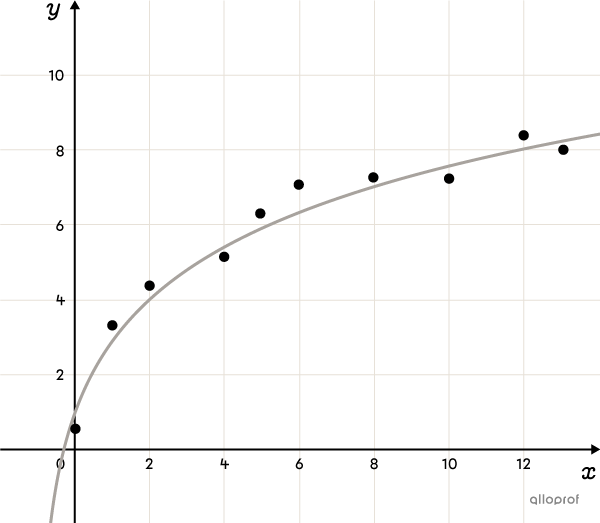
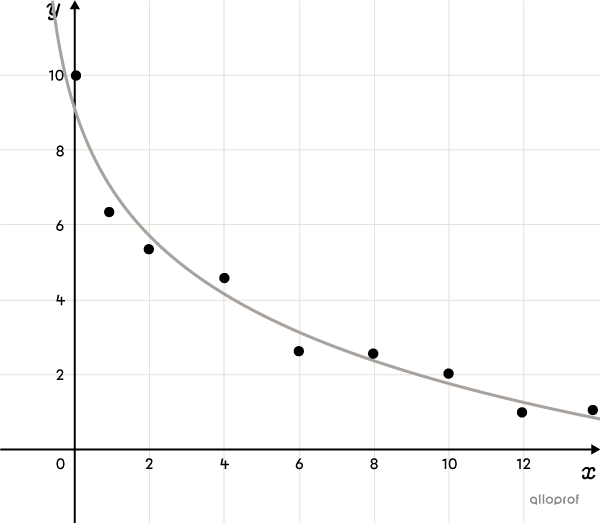
La fonction logarithmique (notion avancée)
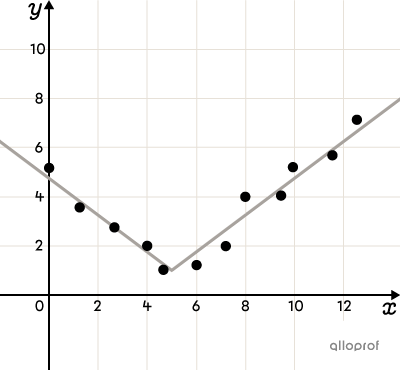
La fonction définie par parties
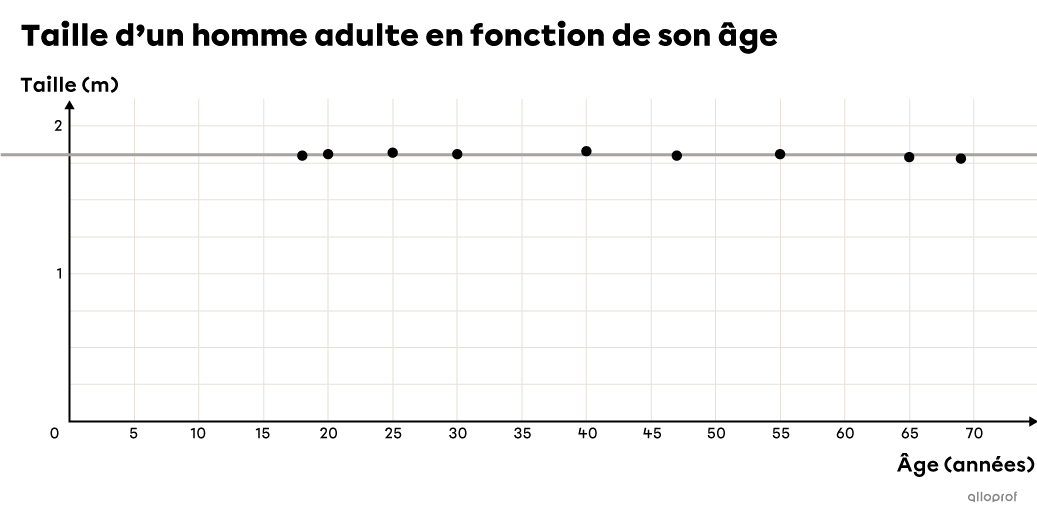
Il arrive qu’un nuage de points ne présente pas une tendance unique. En effet, pour différentes raisons, il peut y avoir une coupure dans les données. Par exemple, un être humain normal grandit pendant les 15 à 20 premières années de sa vie, puis arrête de grandir à l’âge adulte. On observe donc une croissance dans un premier temps, puis une fonction constante par la suite.
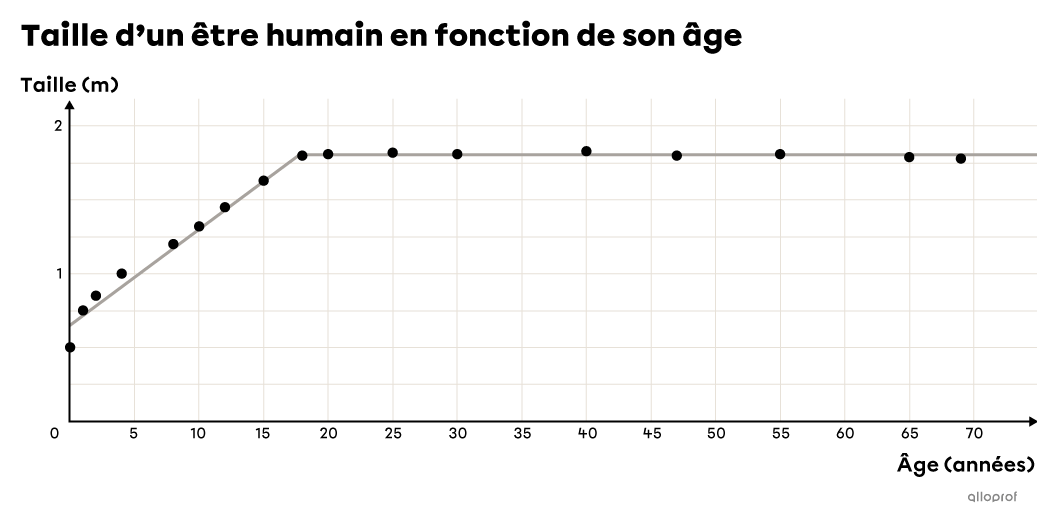
Il existe plusieurs autres fonctions qui peuvent servir à modéliser un nuage de points. En voici quelques-unes.