La réciproque d'une fonction |f| s'obtient en intervertissant les valeurs de |x| et de |y| puis en isolant |y.| Elle se note |f^{-1}.|
On obtient le graphique d'une réciproque en faisant subir à notre fonction une réflexion par rapport à l'axe |y=x.|
Remarque : Il arrive souvent que l'on n'écrive pas le |f^{-1}| et que l'on écrive plutôt |y=.|
Soit une fonction |f| passant par les couples |(-2,-4),| |(-1,-2),| |(0,0),| |(1,2),| |(2,4).|
Alors la réciproque |f^{-1}| passera par les couples |(-4,-2),| |(-2,-1),| |(0,0),| |(2,1),| |(4,2).|
La réciproque d'une fonction n'est pas toujours une fonction.
La réciproque de |f,| notée |f^{-1},| est une fonction si et seulement si aucune droite horizontale (parallèle à l'axe des |x|) ne coupe le graphique de la fonction |f| en plus d'un point.
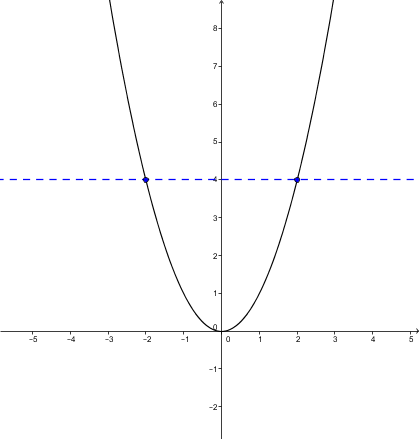
La réciproque de cette fonction n'est pas une fonction.
Comme |f^{-1}| est composée des couples obtenus en intervertissant dans |f| les variables |x| et |y,| on a donc que |\text{ dom } f^{-1} = \text{ima } f| et |\text{ima } f^{-1} = \text{dom } f.| Ainsi, le domaine de |f| devient l'image de |f^{-1}| et vice-versa.
Soit la fonction |f(x)=\dfrac{x}{2}+3| que l'on peut écrire |y=\dfrac{x}{2}+3.|
La réciproque se trouve en intervertissant |x| et |y.| ||y=\dfrac{x}{2} + 3\ \rightarrow\ x = \dfrac{y}{2} + 3||On isole |y.| ||\begin{align}x-3 &= \dfrac{y}{2} \\[3pt] 2(x-3) &= y \\[3pt] 2x-6 &= y\end{align}||Ainsi, la réciproque a pour équation |f^{-1}(x) = 2x-6.|
Voici un graphique représentant la fonction, sa réciproque et l'axe de réflexion.
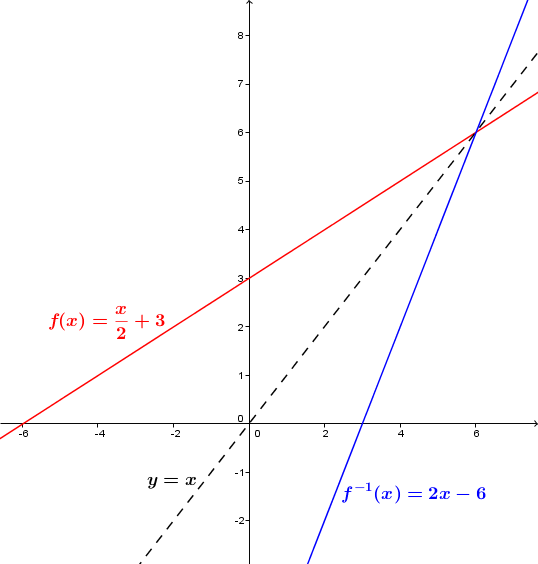
Les réciproques des différentes fonctions :