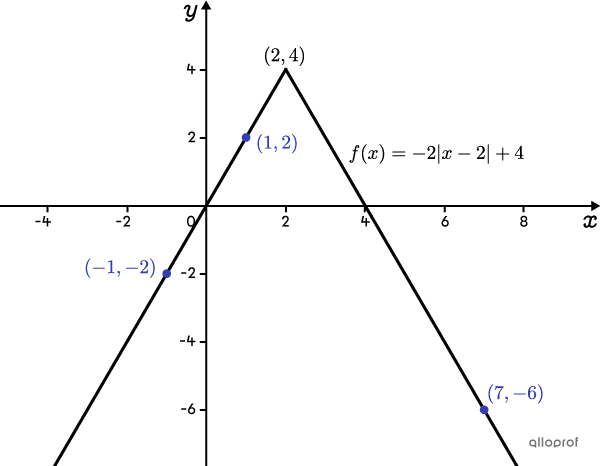Lorsqu’on cherche la règle d’une fonction valeur absolue, 3 cas sont possibles. Dans tous les cas, on utilise la forme canonique simplifiée : |f(x)=a\vert x-h\vert+k.|
Pour trouver la règle d’une fonction valeur absolue lorsqu’on connait les coordonnées du sommet et d’un point quelconque de la fonction, il suffit d’utiliser l’équation sous la forme canonique.
-
Remplacer les paramètres |h| et |k| par les coordonnées du sommet dans la règle.
-
Calculer |a| en remplaçant |x| et |y| par les coordonnées d’un autre point.
-
Écrire la règle.
Détermine la règle de la fonction valeur absolue dont les coordonnées du sommet sont |(-3, -2)| et les coordonnées d'un point sont |(-4, -5).|
-
Remplacer les paramètres |\boldsymbol{h}| et |\boldsymbol{k}| par les coordonnées du sommet dans la règle||\begin{align}f(x)&=a\vert x-\color{#3b87cd}h \vert +\color{#3a9a38}k\\f(x) &=a\vert x-\color{#3b87cd}{-3} \vert +\color{#3a9a38}{-2} \\ f(x) &= a\vert x+3\vert -2 \end{align}||
-
Calculer |\boldsymbol{a}| en remplaçant |\boldsymbol{x}| et |\boldsymbol{y}| par les coordonnées d’un autre point
||\begin{align} \color{#ff55c3}{-5} &= a\vert \color{#ff55c3}{-4}+3\vert -2 \\ -5 &= a\vert -1\vert -2 \\ -5 &= a(1)-2\\ -5 &= a-2\\ -3&=a \end{align}|| -
Écrire la règle
La règle de cette fonction est |f(x)=-3\vert x+3\vert -2.|
Pour trouver la règle d’une fonction valeur absolue lorsqu’on connait 2 points ayant la même ordonnée |(y)| et un autre point de la fonction, on doit trouver la pente des 2 branches de la fonction.
-
Placer les points dans un plan cartésien.
-
Calculer la valeur du paramètre |h| en faisant la moyenne des abscisses |(x)| des 2 points qui ont la même ordonnée |(y).|
-
Calculer la pente de la droite passant par les 2 points qui sont situés du même côté du sommet (sur la même branche).
-
Déterminer le signe du paramètre |a| en analysant l’ouverture de la fonction.
-
Remplacer dans la règle les paramètres |h| et |a| calculés précédemment.
-
Calculer |k| en remplaçant |x| et |y| par les coordonnées d’un point.
-
Écrire la règle.
Dans une fonction valeur absolue, les 2 branches sont symétriques. Ainsi, le paramètre |a| de la fonction valeur absolue, la pente de la branche de gauche |(a_1)| et la pente de la branche de droite |(a_2)| possèdent tous la même valeur si on ne tient pas compte de leur signe.
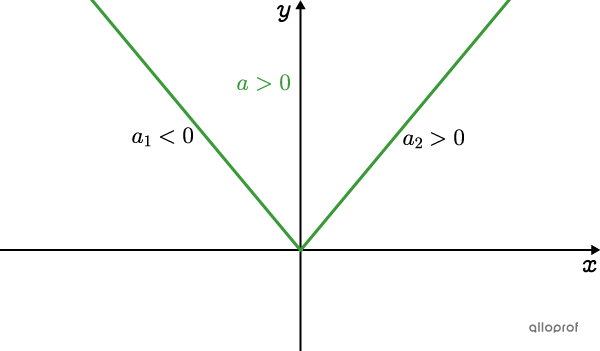
L’ouverture est vers le haut.
-
La pente de la branche de gauche est négative, car elle est décroissante |(a_1<0).|
-
La pente de la branche de droite est positive, car elle est croissante |(a_2>0).|
-
Le paramètre |a| de la fonction valeur absolue est positif |(\color{#3A9A38}{a>0}).|
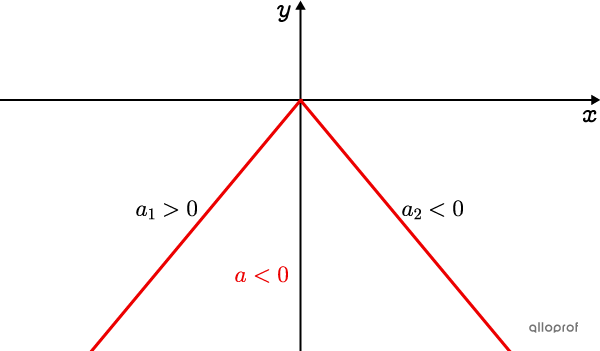
L’ouverture est vers le bas.
-
La pente de la branche de gauche est positive, car elle est croissante |(a_1>0).|
-
La pente de la branche de droite est négative, car elle est décroissante |(a_2<0).|
-
Le paramètre |a| de la fonction valeur absolue est négatif |(\color{#EC0000}{a<0}),| car la courbe a subi une réflexion par rapport à l’axe des |x.|
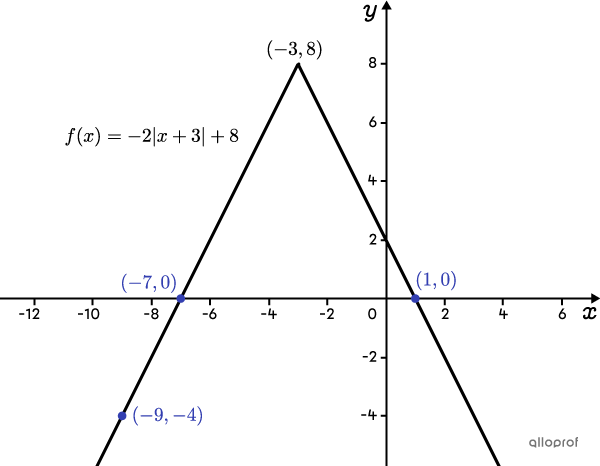
Détermine la règle de la fonction valeur absolue dont les zéros sont |-7| et |1| et qui passe par le point |(-9,-4).|
-
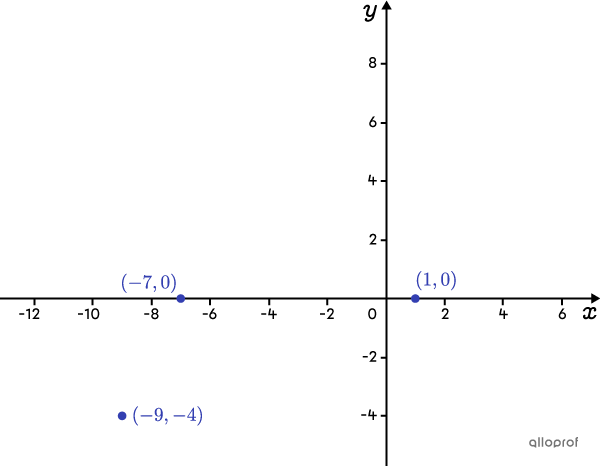
Placer les points dans un plan cartésien
En analysant leur position, on en déduit que les points |(-9,-4)| et |(-7,0)| sont situés sur la même branche de la fonction valeur absolue et que le point |(1,0)| est sur l’autre branche. Aussi, on en déduit que le sommet de la fonction sera au-dessus de l’axe des |x| et que l’ouverture sera vers le bas.
-
Calculer la valeur du paramètre |\boldsymbol{h}| en faisant la moyenne des abscisses des 2 points qui ont la même ordonnée
Dans l’exemple, les points ayant la même ordonnée sont les zéros, situés à |x=-7| et |x=1.| Le |x| du sommet, qui correspond au paramètre |h,| se trouve exactement au milieu des zéros étant donné que le graphique d’une fonction valeur absolue est symétrique. ||\begin{align}h&=\dfrac{-7+1}{2}\\h&=-3\end{align}||
-
Calculer la pente de la droite passant par les 2 points qui sont situés du même côté du sommet
Les points |(-9,-4)| et |(-7,0)| sont situés sur la même branche, à gauche du sommet. On calcule la pente de la droite |(a_1)| passant par ces points. ||\begin{align}a_1&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{0--4}{-7--9} \\ &=2\end{align}||
-
Déterminer le signe du paramètre |\boldsymbol{a}| en analysant l’ouverture de la fonction
Sachant que l’ouverture est vers le bas, on en conclut que |a| est négatif. ||a=-2||
-
Remplacer dans la règle les paramètres |\boldsymbol{h}| et |\boldsymbol{a}| calculés précédemment||\begin{align}f(x)&=\color{#ec0000}a\vert x-\color{#3b87cd}h \vert +k\\f(x) &=\color{#ec0000}{-2}\vert x-\color{#3b87cd}{-3} \vert +k\\ f(x) &=-2\vert x+3 \vert +k\end{align}||
-
Calculer |\boldsymbol{k}| en remplaçant |\boldsymbol{x}| et |\boldsymbol{y}| par les coordonnées d’un point
On prends le point |(1,0).| ||\begin{align} \color{#ff55c3}{0} &= -2\vert \color{#ff55c3}{1}+3\vert +k \\ 0 &= -2\vert 4\vert +k \\ 0 &= -2(4) +k \\ 0&=-8+k \\ 8 &= k \end{align}||
-
Écrire la règle
La règle de cette fonction est |f(x)=-2\vert x+3\vert +8.|
Pour déterminer quels points sont situés sur la même branche lorsqu’on a 3 points quelconques dans le graphique, il y a quelques éléments à respecter.
-
Il ne faut jamais tenir pour acquis que l’un des 3 points est le sommet de la fonction, à moins que ce soit précisé.
-
Il faut toujours s’assurer que la symétrie entre les 2 branches est respectée.
Soit la figure suivante.
Est-ce que ce sont les points |A| et |B| qui sont sur la même branche ou est-ce que ce sont les points |B| et |C|?
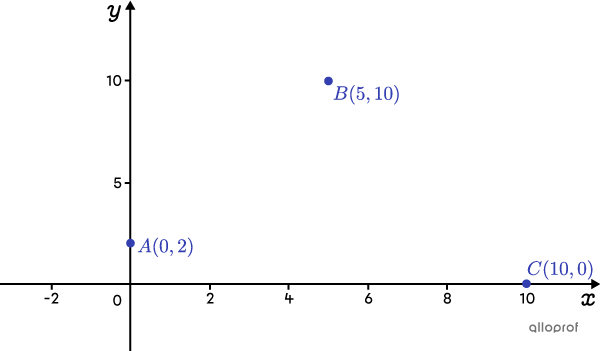
Si |A| et |B| sont sur la même branche, on peut alors calculer la pente de cette branche. ||a_1=\dfrac{10-2}{5-0}=\dfrac{8}{5}||
Comme les 2 branches doivent être symétriques, la pente de la droite symétrique passant par le point |C| est la même, mais négative. ||a_2=-\dfrac{8}{5}||
En traçant la droite |AB| et la droite passant par |C| dont la pente vaut |-\dfrac{8}{5},| on obtient ce graphique.
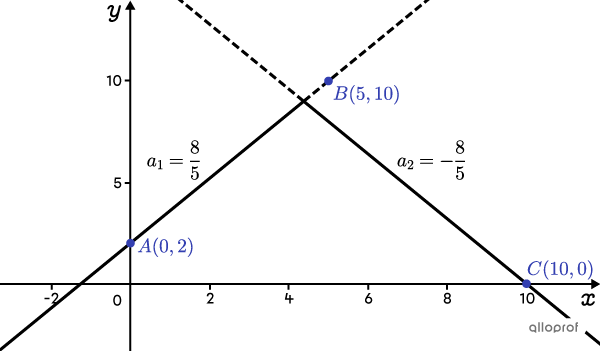
Avec ce choix, on remarque que le sommet est plus bas que le point |B.| Autrement dit, le point |B| n’est situé sur aucune des 2 branches de la valeur absolue, mais plutôt sur le prolongement d’une branche, ce qui veut dire qu’on a fait le mauvais choix.
Si on suppose plutôt que |B| et |C| sont sur la même branche, alors la pente de cette branche est |a_2=\dfrac{10-0}{5-10}=-2.| La pente de la branche de gauche est donc égale à |2| et on obtient le graphique suivant qui confirme que c’est le bon choix.

Dans tous les cas, on remarque que le point |B| n’est pas le sommet de la fonction.
Pour trouver la règle d’une fonction valeur absolue lorsqu’on ne connait ni les coordonnées du sommet ni celles de 2 points situés à la même hauteur (ordonnée) dans le plan cartésien, il faut faire un système d’équations et utiliser la méthode de comparaison. Voici la démarche à suivre.
-
Placer les points dans un plan cartésien.
-
Calculer la pente de la droite passant par les 2 points qui sont situés du même côté du sommet (sur la même branche).
-
Trouver la règle sous la forme |y=ax+b| des 2 branches.
-
Trouver les coordonnées du sommet situé à l’intersection des 2 branches à l’aide de la méthode de comparaison.
-
Déterminer le signe du paramètre |a| en analysant l’ouverture de la fonction.
-
Écrire la règle en remplaçant les paramètres |a,| |h| et |k| par leur valeur.
Détermine la règle de la fonction valeur absolue passant par les points |(1,2),| |(7,-6)| et |(-1,-2).|
-
Placer les points dans un plan cartésien
En analysant leur position, on remarque que les points |(-1,-2)| et |(1,2)| sont situés sur la même branche de la valeur absolue et que le point |(7,-6)| est sur l’autre branche. Aussi, on en déduit que le sommet de la fonction sera au-dessus de l’axe des |x| et que l’ouverture sera vers le bas.
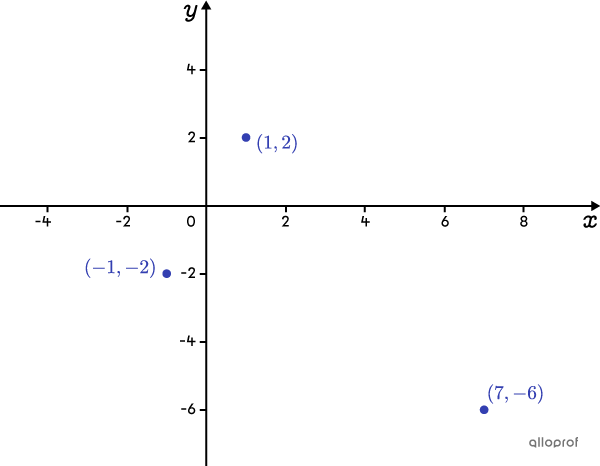
-
Calculer la pente de la droite passant par les 2 points qui sont situés du même côté du sommet
Les 2 points sur la même branche sont |(-1, -2)| et |(1,2).| ||\begin{align}a_1&=\dfrac{y_2-y_1}{x_2-x_1}\\&=\dfrac{2--2}{1--1}\\&=2\end{align}||
-
Trouver la règle sous la forme |\boldsymbol{y=ax+b}| des 2 branches
Pour la branche de gauche, on prend le |a| positif puisque la droite est croissante et on utilise le point |(-1,-2)| pour calculer |b_1.| ||\begin{align} y_1&=a_1x+b_1 \\ -2 &= 2 (-1) + b_1\\ -2 &= -2 + b_1 \\ 0 &=b_1 \end{align}||Donc, pour cette branche, la règle est |y_1=2x.|
Pour la branche de droite, on prend le même |a,| mais négatif. De plus, on utilise le point |(7,-6)| pour calculer |b_2.| ||\begin{align} y_2&=a_2x+b_2 \\ -6 &= -2 (7) + b_2 \\ -6 &= -14 + b_2 \\ 8&=b_2 \end{align}||Donc, pour cette branche, l'équation est |y_2=-2x+8.|
-
Trouver les coordonnées du sommet situé à l’intersection des 2 branches à l’aide de la méthode de comparaison ||\begin{align} y_1&=y_2 \\ 2x &= -2x + 8 \\ 4x&=8\\x&=2 \end{align}||Donc, |h=2.|
Pour |k,| on remplace |x| par |2| dans l'une ou l'autre des 2 règles. ||\begin{align} \begin{aligned}y_1 &= 2x \\ &= 2 (2) \\ &=4\end{aligned}\quad\ \ \begin{aligned}y_2 &= -2x+8 \\ &= -2 (2)+8 \\ &=4\end{aligned} \end{align}||Donc, |k=4.|
-
Déterminer le signe du paramètre |\boldsymbol{a}| en analysant l’ouverture de la fonction valeur absolue
Sachant que l’ouverture est vers le bas, on en conclut que |a| est négatif.
Donc, |a=-2.|
-
Écrire la règle en remplaçant les paramètres |\boldsymbol{a},| |\boldsymbol{h}| et |\boldsymbol{k}| par leur valeur
En utilisant la règle sous la forme canonique, on obtient ceci. ||\begin{align}f(x)&=a\vert x-h\vert +k\\\\f(x)&=-2\vert x-2\vert +4\end{align}||