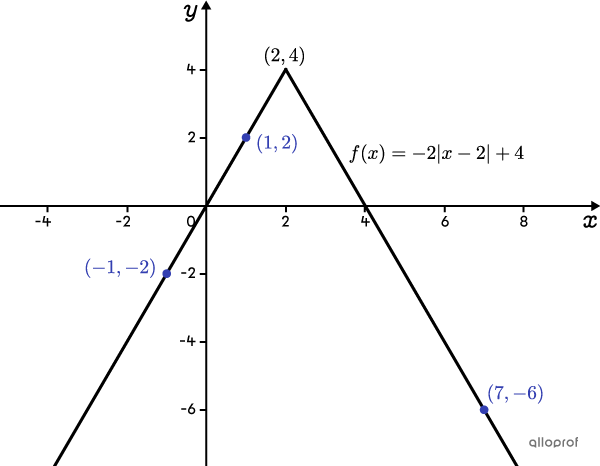When looking for the rule of an absolute value function, there are 3 possible cases. In each case, use the simplified functional form: |f(x)=a\vert x-h\vert+k.|
To find the rule of an absolute value function when we know the coordinates of the vertex and any other point of the function, use the equation in functional form.
-
Replace parameters |h| and |k| with the coordinates of the vertex.
-
Calculate |a| by replacing |x| and |y| with the coordinates of the other point.
-
Write the rule.
Determine the rule of the absolute value function with a vertex of |(-3, -2)| and another point where the coordinates are |(-4, -5).|
-
Replace parameters |\boldsymbol{h}| and |\boldsymbol{k}| with the coordinates of the vertex
||\begin{align}f(x)&=a\vert x-\color{#3b87cd}h \vert +\color{#3a9a38}k\\f(x) &=a\vert x-\color{#3b87cd}{-3} \vert +\color{#3a9a38}{-2} \\ f(x) &= a\vert x+3\vert -2 \end{align}|| -
Calculate |\boldsymbol{a}| by replacing |\boldsymbol{x}| and |\boldsymbol{y}| with the coordinates of the other point
||\begin{align} \color{#ff55c3}{-5} &= a\vert \color{#ff55c3}{-4}+3\vert -2 \\ -5 &= a\vert -1\vert -2 \\ -5 &= a(1)-2\\ -5 &= a-2\\ -3&=a \end{align}|| -
Write the rule
The rule of the function is |f(x)=-3\vert x+3\vert -2.|
To find the rule of an absolute value function when we know 2 points with the same |(y)|-value and a third point, we must find the slope of the function’s 2 branches.
-
Plot the points on the Cartesian plane.
-
Calculate the value of parameter |h| by calculating the average of the |x|-values of the 2 points with the same |y|-value.
-
Calculate the slope of the line passing through the 2 points located on the same side of the vertex (on the same branch).
-
Determine the sign of parameter |a| by analyzing if the function opens upwards or downwards.
-
Replace the values of parameters |h| and |a| calculated in Step 4.
-
Calculate |k| by replacing |x| and |y| with the coordinates of a point.
-
Write the rule.
In an absolute value function, the 2 branches are symmetrical. So, parameter |a|, the slope of the left branch |(a_1),| and the slope of the right branch |(a_2)| all have the same value if we ignore the signs.
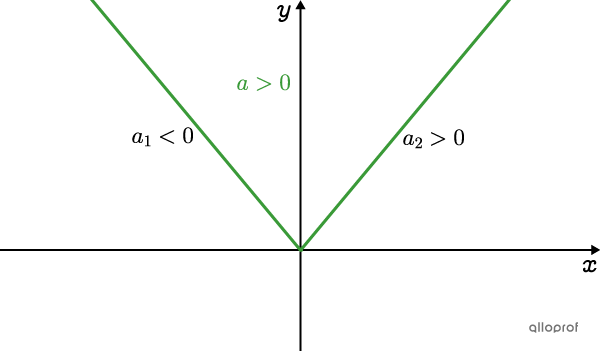
The Opening is Upwards
-
The slope of the left branch is negative as it is decreasing |(a_1<0).|
-
The slope of the right branch is positive as it is increasing |(a_2>0).|
-
Parameter |a| of the absolute value function is positive |(\color{#3A9A38}{a>0}).|
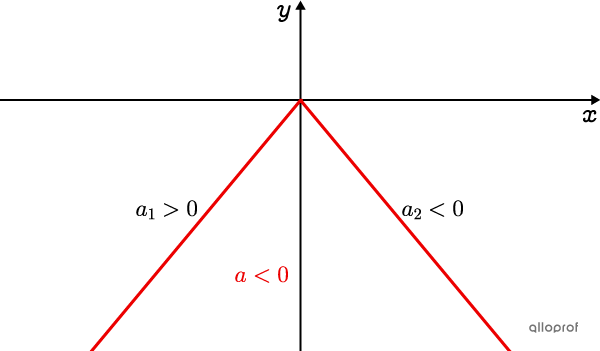
The Opening is Downwards
-
The slope of the left branch is positive as it is increasing |(a_1>0).|
-
The slope on the right branch is negative as it is decreasing |(a_2<0).|
-
Parameter |a| of the absolute value function is negative |(\color{#EC0000}{a<0}),| because the curve has been reflected across the |x|-axis.
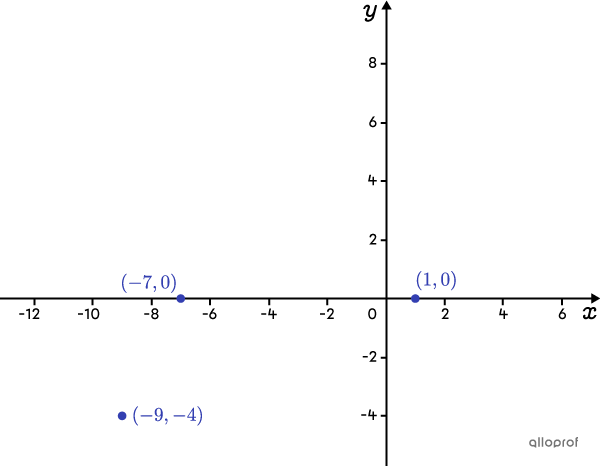
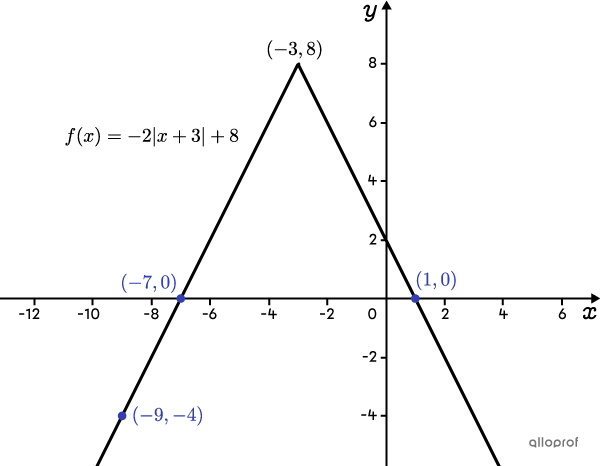
Determine the rule for the absolute value function where the zeros are |-7| and |1,| and passes through the point |(-9,-4).|
-
Plot the points on the Cartesian plane
Analyzing their position, points |(-9,-4)| and |(-7,0)| are located on the same branch of the absolute value function and point |(1,0)| is on the other branch. Therefore, the vertex of the function is above the |x|-axis and the graph opens downwards.
-
Calculate the value of parameter |\boldsymbol{h}| by calculating the average of the |\boldsymbol{x}|-values of the 2 points with the same |\boldsymbol{y}|-value.
In this case, the two points with the same y-value are the zeros located at |x=-7| and |x=1.| The |x| value of the vertex corresponding to parameter |h| is exactly in the middle of the two zeros, because the graph of an absolute value function is symmetrical. ||\begin{align}h&=\dfrac{-7+1}{2}\\h&=-3\end{align}||
-
Calculate the slope of the line passing through the 2 points located on the same side of the vertex (on the same branch)
The points |(-9,-4)| and |(-7,0)| are located on the same branch to the left of the vertex. Calculating the slope of the line |(a_1)| passing through the points:
||\begin{align}a_1&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{0--4}{-7--9} \\ &=2\end{align}|| -
Determine the sign of parameter |\boldsymbol{a}| by analyzing if the function opens upwards or downwards
Since the graph opens downwards, parameter |a| must be negative.
|a=-2|
-
Replace the values of parameters |\boldsymbol{h}| and |\boldsymbol{a}| calculated in Step 4||\begin{align}f(x)&=\color{#ec0000}a\vert x-\color{#3b87cd}h \vert +k\\f(x) &=\color{#ec0000}{-2}\vert x-\color{#3b87cd}{-3} \vert +k\\ f(x) &=-2\vert x+3 \vert +k\end{align}||
-
Calculate |\boldsymbol{k}| by replacing |\boldsymbol{x}| and |\boldsymbol{y}| by the coordinates of a point
We use the point |(1,0):|
||\begin{align} \color{#ff55c3}{0} &= -2\vert \color{#ff55c3}{1}+3\vert +k \\ 0 &= -2\vert 4\vert +k \\ 0 &= -2(4) +k \\ 0&=-8+k \\ 8 &= k \end{align}||
-
Write the rule
The rule for this absolute value function is |f(x)=-2\vert x+3\vert +8.|
To determine which points are on the same branch when 3 points on the graph, there are a few things to keep in mind:
-
Never assume any of the given 3 points is the function’s vertex, unless specified.
-
Always make sure that the symmetry between the 2 branches is respected.
Consider the following figure:
Are the points |A| and |B| on the same branch, or are points |B| and |C|?
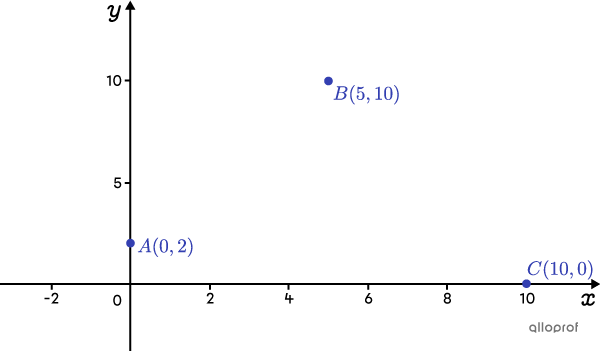
If |A| and |B| are on the same branch, the slope of the branch can be calculated: ||a_1=\dfrac{10-2}{5-0}=\dfrac{8}{5}||
Since the 2 branches must be symmetrical, the slope of the other branch passing through the point |C| is the same, but negative. ||a_2=-\dfrac{8}{5}||
Next, graph the line |AB| and the line passing through |C,| where the slope is |-\dfrac{8}{5}.|
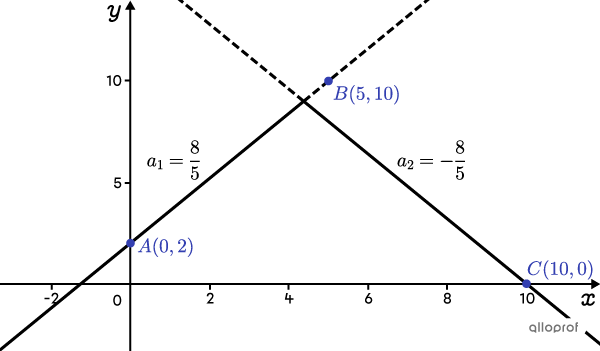
Note that the vertex is lower than the point |B.| In other words, point |B| is not located on either of the 2 branches of the absolute value function, but on an extension of a branch, which does not make sense. This means that points |A| and |B| are not on the same branch.
If |B| and |C| were instead on the same branch, the slope of the branch can be calculated: |a_2=\dfrac{10-0}{5-10}=-2.| Therefore, the slope of the left branch is equal to |2| and we obtain the following graph which confirms it is the right choice.

Note that in each case, point |B| is not the vertex of the function.
To find the rule of an absolute value function when we don’t know the coordinates of the vertex or have 2 points located at the same height (same y-coordinate) on the Cartesian plane, we create a system of equations and use the comparison method to solve it. An example is written below.
-
Plot the points on the Cartesian plane.
-
Calculate the slope of the line passing through the 2 points on the same side of the vertex (on the same branch).
-
Find the rule in the form |y=ax+b| of the 2 branches.
-
Find the coordinates of the vertex (i.e., the intersection point of the two branches) using the comparison method.
-
Determine the sign of parameter |a| by analyzing the opening of the function.
-
Write the rule by replacing the values of parameters |a,| |h,| and |k.|
Find the rule of the absolute value function passing through the points |(1,2),| |(7,-6,)| and |(-1,-2).|
-
Plot the points on the Cartesian plane
Analyzing their position, points |(-1,-2)| and |(1,2)| are located on the same branch, and point |(7,-6)| is on the other branch of the absolute value function graph. Therefore, the vertex of the function will be above the |x|-axis and it will open downwards.
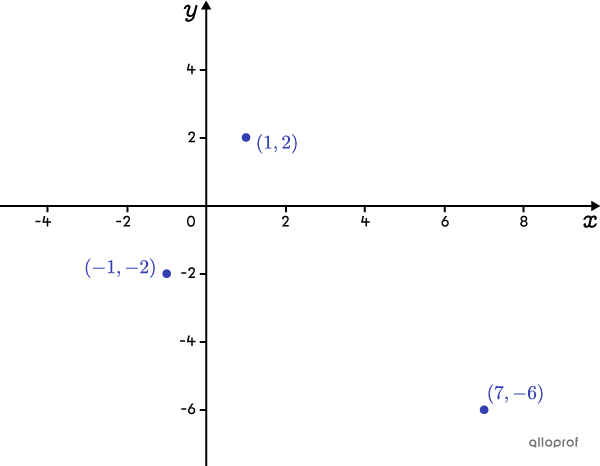
-
Calculate the slope of the line passing through the 2 points on the same side of the vertex (on the same branch)
The 2 points on the same branch are |(-1, -2)| and |(1,2).|
||\begin{align}a_1&=\dfrac{y_2-y_1}{x_2-x_1}\\&=\dfrac{2--2}{1--1}\\&=2\end{align}|| -
Find the rule in the form |\boldsymbol{y=ax+b}| of the 2 branches
For the left branch, |a| is positive as the line is increasing. Using the point |(-1,-2)| to calculate |b_1:|
||\begin{align} y_1&=a_1x+b_1 \\ -2 &= 2 (-1) + b_1\\ -2 &= -2 + b_1 \\ 0 &=b_1 \end{align}||
So, the rule for this branch is |y_1=2x.|For the right branch, |a| is the same but negative. Using the point |(7,-6)| to calculate |b_2:|
||\begin{align} y_2&=a_2x+b_2 \\ -6 &= -2 (7) + b_2 \\ -6 &= -14 + b_2 \\ 8&=b_2 \end{align}||
So, the rule for this branch is |y_2=-2x+8.| -
Find the coordinates of the vertex (i.e., the intersection point of the two branches) using the comparison method||\begin{align} y_1&=y_2 \\ 2x &= -2x + 8 \\ 4x&=8\\x&=2 \end{align}||
So, |h=2.|
To find |k,| replace |x| by |2| in either of the 2 rules. ||\begin{align} \begin{aligned}y_1 &= 2x \\ &= 2 (2) \\ &=4\end{aligned}\quad \begin{aligned}y_2 &= -2x+8 \\ &= -2 (2)+8 \\ &=4\end{aligned} \end{align}||
So, |k=4.| -
Determine the sign of parameter |\boldsymbol{a}| by analyzing the opening of the function
Since the opening is downwards, parameter |a| is negative.
So, |a=-2.|
-
Write the rule by replacing the values of parameters |\boldsymbol{a,}| |\boldsymbol{h,}| and |\boldsymbol{k}|
Replacing the values in the functional form of the rule of an absolute value function:||\begin{align}f(x)&=a\vert x-h\vert +k\\f(x)&=-2\vert x-2\vert +4\end{align}||