Pour résoudre un problème à l’aide de la fonction affine, il faut généralement trouver la règle de la fonction et résoudre une équation de degré 1.
||y=ax+b||où
|a :| taux de variation
|b :| ordonnée à l’origine
Voici les étapes principales à suivre pour y arriver.
-
Identifier la variable indépendante et la variable dépendante.
-
Trouver la règle.
-
Trouver le paramètre a.
-
Trouver le paramètre b.
-
-
Remplacer la donnée fournie dans la règle.
-
Isoler l’autre variable.
-
Répondre à la question.
-
Pour bien visualiser la situation, il est aidant de tracer la fonction dans un plan cartésien ou de se faire une esquisse de la situation. Bien que le graphique ne soit pas assez précis pour obtenir une réponse, il permet de vérifier que les données trouvées fonctionnent dans le contexte de la situation.
-
Il arrive que le taux de variation et la valeur initiale soient fournis directement dans la mise en situation. Dans ce cas, il n’est pas nécessaire de les calculer.
Éric vient de trouver un nouvel emploi comme cueilleur de fraises à l’Île d’Orléans. Lors de sa première journée, il remarque que l'ancien cueilleur lui a laissé un certain nombre de paniers de fraises. À la fin de la journée, il y a déjà un total de |31| paniers remplis.
Considérant qu’Éric travaille |6| heures par jour et qu’il est capable de remplir |3| paniers en |1| heure, réponds aux questions suivantes.
Question 1 : Quel sera le nombre total de paniers de fraises remplis après |5| jours de travail?
Question 2 : Après combien de jours de travail aura-t-il rempli un total de |157| paniers?
-
Identifier la variable indépendante et la variable dépendante
On s’intéresse à la quantité de paniers de fraises remplis en fonction du temps.
|x :| temps (en heures)
|y :| nombre de paniers de fraises remplis -
Trouver la règle
-
Trouver le paramètre |\boldsymbol{a}|
On indique dans le problème qu’Éric remplit |3| paniers chaque heure. Il s’agit du taux de variation.||a=3|| -
Trouver le paramètre |\boldsymbol{b}|
L’ordonnée à l’origine représente la valeur initiale. Dans le contexte, cela signifie la quantité de paniers de fraises qui étaient remplis avant même qu’Éric commence sa première cueillette. Pour la trouver, on remplace, dans la règle, le paramètre |a| par |3| et on remplace |x| et |y| par un couple fourni. On sait qu’après sa première journée, il y a |31| paniers. De plus, comme il travaille |6| heures par jour, on en déduit le couple |(6,31).|||\begin{align}y&=ax+b\\y&=3x+b\\\\\color{#3a9a38}{31}&=3(\color{#3a9a38}6)+b\\31&=18+b\\31\color{#ec0000}{-18}&=18+b\color{#ec0000}{-18}\\13&=b\end{align}||
La règle de la fonction est donc |y=3x+13.|
-
Question 1 : Quel sera le nombre total de paniers de fraises remplis après |\boldsymbol{5}| jours de travail?
-
Remplacer la donnée fournie dans la règle
La donnée fournie est une donnée de temps, donc une valeur de |x.| On doit ainsi remplacer |x| dans la règle et trouver la valeur de |y| correspondante. Toutefois, il est d’abord nécessaire de convertir |5| jours en heures, puisque les unités de mesure du taux de variation sont des |\text{paniers/heure}.| Comme Éric travaille |6| heures par jour, |5| jours représentent |5\times6=30| heures de travail. On remplace donc |x| par |30.|||y=3(30)+13|| -
Isoler l’autre variable
Puisque |y| est déjà isolé, on complète seulement le calcul.||\begin{align}y&=3\times30+13\\&=90+13\\&=103\end{align}|| -
Répondre à la question
Après |5| jours de travail, il y aura un total de |103| paniers de fraises.
Question 2 : Après combien de jours de travail aura-t-il rempli un total de |\boldsymbol{157}| paniers?
-
Remplacer la donnée fournie dans la règle
La donnée fournie est un nombre de paniers, donc une valeur de |y.| On doit ainsi remplacer |y| dans la règle et trouver la valeur de |x| correspondante. ||157=3x+13|| -
Isoler l’autre variable
||\begin{align}157&=3x+13\\157\color{#ec0000}{-13}&=3x+13\color{#ec0000}{-13}\\144&=3x\\\color{#ec0000}{\dfrac{\color{black}{144}}{3}}&=\color{#ec0000}{\dfrac{\color{black}{3x}}{3}}\\48&=x\end{align}|| -
Répondre à la question
On sait qu’après |48| heures de travail, il y aura |157| paniers. Par contre, la question demande un nombre de jours. Il faut donc diviser le nombre d’heures par |6,| puisqu’Éric travaille |6| heures par jour. ||48\ \text{heures}\div6\ \text{heures/jour}=8\ \text{jours}|| Il y aura donc |157| paniers de fraises remplis après |8| jours de travail.
Henri est laveur de vitres. Une compagnie veut l’engager pour nettoyer les vitres de son bureau dans un gratte-ciel situé au centre-ville. Elle lui propose 2 options de rémunération.
-
Un montant fixe de |2\ 205\ $,| peu importe le nombre de vitres nettoyées.
-
Un montant de base de |500\ $| avec un supplément de |2{,}75\ $| par vitre nettoyée.
Sachant que le gratte-ciel en question comporte |593| vitres, réponds aux questions suivantes.
Question 1 : Quelle option est la plus avantageuse pour Henri?
Question 2 : Combien de vitres doit nettoyer Henri pour que les 2 options soient équivalentes?
-
Identifier la variable indépendante et la variable dépendante
On s’intéresse au montant gagné par Henri en fonction du nombre de vitres nettoyées.
|x :| nombre de vitres nettoyées
|y :| montant gagné ($) -
Trouver la règle
La règle de la 1re proposition est une fonction polynomiale de degré |0.| En effet, elle n’a pas de pente, puisque le montant ne varie pas. Sa règle est |f(x)=2\ 205.|
On peut ensuite trouver la règle de la 2e proposition.-
Trouver le paramètre |\boldsymbol{a}|
On indique dans l’énoncé qu’Henri est payé |2{,}75\ $| par vitre nettoyée. Il s’agit du taux de variation.
||a=2{,}75|| -
Trouver le paramètre |\boldsymbol{b}|
L’ordonnée à l’origine représente le montant qu’Henri recevra avant même d’avoir commencé à laver les vitres.
||b=500||
La règle de la fonction est donc |y=2{,}75x+500.|
-
Question 1 : Quelle option est la plus avantageuse pour Henri?
Il faut se demander si la 2e proposition est plus payante que la 1re. Pour le déterminer, on doit donc chercher quel serait le montant gagné par Henri avec la 2e option s’il nettoyait |593| vitres.
-
Remplacer la donnée fournie dans la règle
On fournit un nombre de vitres nettoyées, donc une valeur de |x.| On doit ainsi remplacer |x| dans la règle et trouver la valeur de |y| correspondante.||y=2{,}75(593)+500|| -
Isoler l’autre variable
Puisque |y| est déjà isolé, on complète seulement le calcul.||\begin{align}y&=2{,}75\times593+500\\&=1\ 630{,}75+500\\&=2\ 130{,}75\end{align}|| -
Répondre à la question
Puisque |2\ 130{,}75<2\ 205,| il est plus avantageux pour Henri de choisir la 1re proposition.
Question 2 : Combien de vitres doit nettoyer Henri pour que les 2 options soient équivalentes?
On cherche le nombre de vitres à nettoyer pour avoir un salaire de |2\ 205\ $| avec la 2e proposition.
-
Remplacer la donnée fournie dans la règle
La donnée fournie est un salaire, donc une valeur de |y.| On doit ainsi remplacer |y| dans la règle et trouver la valeur de |x| correspondante.||2\ 205=2{,}75x+500|| -
Isoler l’autre variable
||\begin{align}2\ 205&=2{,}75x+500\\2\ 205\color{#ec0000}{-500}&=2{,}75x+500\color{#ec0000}{-500}\\1\ 705&=2{,}75x\\\color{#ec0000}{\dfrac{\color{black}{1\ 705}}{2{,}75}}&=\color{#ec0000}{\dfrac{\color{black}{2{,}75x}}{2{,}75}}\\620&=x\end{align}|| -
Répondre à la question
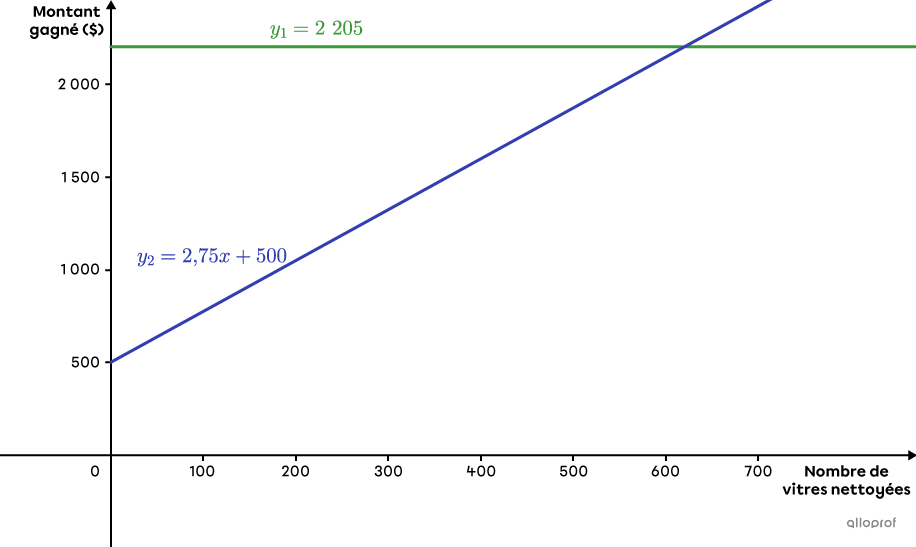
Les 2 options sont parfaitement équivalentes si Henri lave |620| vitres. S’il en nettoie moins, la 1re option est plus avantageuse et s’il en lave plus, c’est la 2e option qui le sera.
Voici la représentation graphique de la situation.
Virginie et Gabrielle aiment beaucoup la lecture et elles lisent le même roman en même temps. Au moment où elles se parlent du livre pour la 1re fois, Virginie avait déjà lu |50| pages et elle lisait à un rythme de |28| pages tous les |5| jours. Gabrielle avait lu |36| pages et était rendue à |78| pages après |6| jours. On suppose que le rythme de lecture des |2| amies ne change pas tout au long de la lecture. Réponds aux questions suivantes.
Question 1 : Si le livre comporte |246| pages, qui le terminera en premier?
Question 2 : À ce moment-là, combien de pages restera-t-il à lire à l’autre amie?
On commence par trouver les règles associées au rythme de lecture des |2| amies.
-
Identifier la variable indépendante et la variable dépendante
On s’intéresse au nombre de pages lues en fonction du temps, en jours.
|x :| temps (jours)
|y :| nombre de pages lues -
Trouver les règles
On commence par celle de Virginie.-
Trouver le paramètre |\boldsymbol{a}|
On indique dans le problème qu’elle lit |28| pages tous les |5| jours. Il s’agit du taux de variation.||a=\dfrac{28}{5}|| -
Trouver le paramètre |\boldsymbol{b}|
L’ordonnée à l’origine représente le nombre de pages lues au moment où les amies se sont parlé du livre pour la première fois.||b=50||
La règle de la fonction pour Virginie est donc |y_v=\dfrac{28}{5}x+50.|
On trouve maintenant la règle de la fonction pour Gabrielle.
-
Trouver le paramètre |\boldsymbol{a}|
On indique dans le problème qu’elle avait lu |36| pages au moment où elle a parlé du livre pour la première fois avec son amie et qu’après |6| jours, elle était rendue à la page |78.| Il faut donc calculer le taux de variation à l’aide des couples |(0,36)| et |(6,78).|||\begin{align}a&=\dfrac{y_2-y_1}{x_2-x_1}\\&=\dfrac{78-36}{6-0}\\&=\dfrac{42}{6}\\&=7\end{align}|| -
Trouver le paramètre |\boldsymbol{b}|
L’ordonnée à l’origine représente le nombre de pages lues au moment où les amies se sont parlé du livre pour la première fois.||b=36||
La règle de la fonction pour Gabrielle est donc |y_g=7x+36.|
-
Question 1 : Si le livre comporte |\boldsymbol{246}| pages, qui le terminera en premier?
On cherche le nombre de jours que prendra chaque fille pour lire les |246| pages.
-
Remplacer la donnée fournie dans la règle
On fournit un nombre de pages, donc une valeur de |y.| On doit ainsi remplacer |y| dans les règles et trouver les valeurs de |x| correspondantes.
Virginie||246=\dfrac{28}{5}x+50||
Gabrielle||246=7x+36||
-
Isoler l’autre variable
Virginie||\begin{align}246\color{#ec0000}{-50}&=\dfrac{28}{5}x+50\color{#ec0000}{-50}\\196&=\dfrac{28}{5}x\\
196\color{#ec0000}{\times 5}&=\dfrac{28}{5}x\color{#ec0000}{\times 5}\\980&=28x\\\color{#ec0000}{\dfrac{\color{black}{980}}{28}}&=\color{#ec0000}{\dfrac{\color{black}{28x}}{28}}\\35&=x\end{align}||
Gabrielle||\begin{align}246\color{#ec0000}{-36}&=7x+36\color{#ec0000}{-36}\\210&=7x\\\color{#ec0000}{\dfrac{\color{black}{210}}{7}}&=\color{#ec0000}{\dfrac{\color{black}{7x}}{7}}\\30&=x\end{align}||
-
Répondre à la question
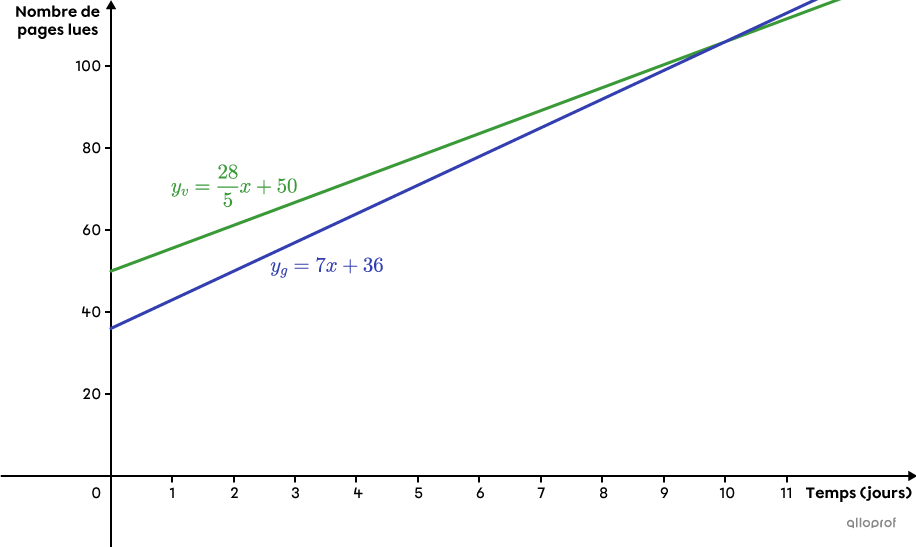
C’est Gabrielle qui terminera le livre en premier après |30| jours, alors que Virginie le terminera après |35| jours.
Question 2 : À ce moment-là, combien de pages restera-t-il à lire à l’autre amie?
Il faut trouver le nombre de pages que Virginie aura lues après |30| jours.
-
Remplacer la donnée fournie dans la règle
La donnée fournie est un nombre de jours, donc une valeur de |x.| On doit ainsi remplacer |x| dans la règle de Virginie et trouver la valeur de |y| correspondante.||y_v=\dfrac{28}{5}(30)+50|| -
Isoler l’autre variable
||\begin{align}y_v&=\dfrac{28}{5}\times30+50\\&=\dfrac{840}{5}+50\\&=168+50\\&=218\end{align}|| -
Répondre à la question
Comme on demande le nombre de pages restantes, on doit faire une soustraction.||246-218=28||Lorsque Gabrielle aura terminé sa lecture, il restera |28| pages à lire à Virginie.
Voici la représentation graphique de la situation.
Pour valider ta compréhension à propos de la résolution de problèmes à l’aide de la fonction affine de façon interactive, consulte la MiniRécup suivante.
