To solve a problem with the linear function, we find the rule of the function and solve a first-degree equation.
||y=ax+b|| where
|a:| rate of change
|b:| |y|-intercept
Here are the main steps to follow.
-
Determine the independent variable and the dependent variable.
-
Find the rule.
-
Find parameter a.
-
Find parameter b.
-
-
Replace the given value into the rule.
-
Isolate the other variable.
-
Answer the question.
-
To visualize the situation, graph the function on a Cartesian plane or sketch the situation. Although the graph is not accurate enough to find the answer, it enables you to check whether the data found works in the context.
-
Sometimes the rate of change and the initial value are given directly in the context of the problem. In this case, it is not necessary to calculate them.
Eric has just found a new job as a strawberry picker on Île d'Orléans. On his first day, he discovers that the previous picker left him a number of baskets full of strawberries. At the end of the day, Eric has a total of |31| full baskets.
Knowing that Eric works |6| hours a day and can fill |3| baskets in |1| hour, answer the following questions.
Question 1: What is the total number of strawberry baskets Eric will fill after |5| days of work?
Question 2: After how many days of work will he fill a total of |157| baskets?
-
Determine the independent variable and the dependent variable
We're looking for the quantity of filled strawberry baskets regarding the time.
|x:| time (hours)
|y:| number of filled strawberry baskets -
Find the rule
-
Find parameter |\boldsymbol{a}|
The problem states that Eric fills |3| baskets every hour. This is the rate of change.
||a=3|| -
Find parameter |\boldsymbol{b}|
The |y|-intercept is the initial value. In context, this is the quantity of strawberry baskets filled before Eric started picking. To find the quantity, we replace the parameter |a| with |3| in the rule and replace |x| and |y| with a given point. After his first day, there are |31| baskets. He works |6| hours per day, therefore, we can determine that |(6,31)| is a point.
||\begin{align}y&=ax+b\\y&=3x+b\\\\\color{#3a9a38}{31}&=3(\color{#3a9a38}6)+b\\31&=18+b\\31\color{#ec0000}{-18}&=18+b\color{#ec0000}{-18}\\13&=b\end{align}||
The rule of the function is therefore |y=3x+13.|
-
Question 1: What is the total number of strawberry baskets filled after |5| days of work?
-
Replace the given value into the rule
The given value is a time, so it is an |x|-value. We must therefore replace |x| in the rule and find the corresponding |y|-value. However, first we must convert |5| days to hours, since the measurement units for the rate of change are |\text{baskets/hour}.| Since Eric works |6| hours per day, |5| days represent |5\times6=30| hours of work. We therefore replace |x| by |30.|
||y=3(30)+13|| -
Isolate the other variable
Since |y| is already isolated, we simply complete the calculation.
||\begin{align}y&=3\times30+13\\&=90+13\\&=103\end{align}|| -
Answer the question
After |5| days of work, there will be a total of |103| strawberry baskets filled.
Question 2: After how many days of work will he have filled a total of |\boldsymbol{157}| baskets?
-
Replace the given value into the rule
The given value is a number of baskets, so a |y|-value. Replace |y| in the rule and find the corresponding |x|-value.
||157=3x+13|| -
Isolate the other variable
||\begin{align}157&=3x+13\\157\color{#ec0000}{-13}&=3x+13\color{#ec0000}{-13}\\144&=3x\\\color{#ec0000}{\dfrac{\color{black}{144}}{3}}&=\color{#ec0000}{\dfrac{\color{black}{3x}}{3}}\\48&=x\end{align}|| -
Answer the question
We know that after |48| hours of work, there will be |157| baskets. However, the question asks for a number of days. So we must divide the number of hours by |6,| since Eric works |6| hours per day. ||48\ \text{hours}\div6\ \text{hours/day}=8\ \text{days}|| Therefore, there will be |157| baskets of strawberries filled after |8| days of work.
Henry is a window cleaner. A company wants to hire him to clean office windows on a downtown skyscraper. They offer him 2 remuneration options.
-
A flat rate of |$2\ 205,| regardless of the number of windows cleaned.
-
A base amount of |$500| with an extra |$2.75| per window cleaned.
Given that the company’s skyscraper has |593| windows, answer the following questions.
Question 1: Which option is best for Henry?
Question 2: How many windows must Henry clean for the 2 options to be equivalent?
-
Determine the independent variable and the dependent variable
We want to know the amount earned by Henry regarding the number of windows cleaned.
|x:| number of windows cleaned
|y:| amount earned ($) -
Find the rule
The rule for the first option is a zero-degree polynomial (constant) function. The slope is |0| since the amount does not vary. Its rule is |f(x)=2\ 205.|
We can now find the rule of the second option.-
Find parameter |\boldsymbol{a}|
The problem states that Henry is paid |$2.75| per window cleaned. It is the rate of change.
||a=2.75|| -
Find parameter |\boldsymbol{b}|
The initial value represents the amount of money Henry will receive before he has even started washing the windows.
||b=500||
The rule of the function is therefore |y=2.75x+500.|
-
Question 1: Which option is best for Henry?
The question is whether the second option pays better than the first. We need to find out how much Henry would earn with the second option if he cleaned |593| windows.
-
Replace the given value into the rule
The number of cleaned windows is given, so an |x|-value is given. We have to replace |x| in the rule and find the corresponding |y|-value.
||y=2.75(593)+500|| -
Isolate the other variable
Since |y| is already isolated, simply complete the calculation.
||\begin{align}y&=2.75\times593+500\\&=1\ 630.75+500\\&=2\ 130.75\end{align}|| -
Answer the question
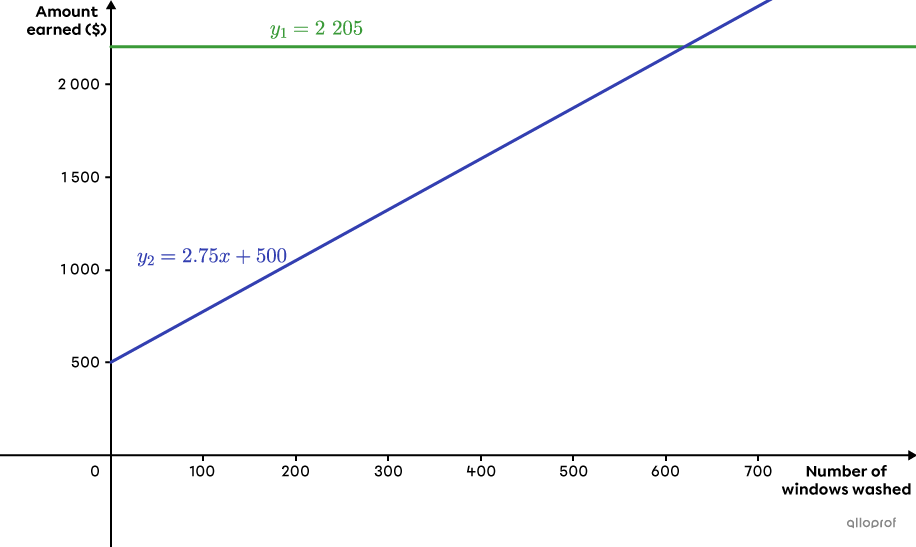
Since |2\ 130.75<2\ 205,| the 1st option works best for Henry.
Question 2: How many windows must Henry clean for the 2 options to be equivalent?
We are looking for the number of windows to clean to earn |$2\ 205| with the 2nd option.
-
Replace the given value into the rule
The given value is a salary, so a |y|-value. Replace |y| in the rule and find the corresponding |x|-value.
||2\ 205=2.75x+500|| -
Isolate the other variable
||\begin{align}2\ 205&=2.75x+500\\2\ 205\color{#ec0000}{-500}&=2.75x+500\color{#ec0000}{-500}\\1\ 705&=2.75x\\\color{#ec0000}{\dfrac{\color{black}{1\ 705}}{2.75}}&=\color{#ec0000}{\dfrac{\color{black}{2.75x}}{2.75}}\\620&=x\end{align}|| -
Answer the question
The 2 options are equivalent if Henry washes |620| windows. If he cleans less, the 1st option is better and if he cleans more, the 2nd option is better.
The following is a graphical representation of the situation.
Amina and Gabrielle enjoy reading. They decide to read the same novel at the same time for fun. When they get together to talk about the book for the first time, Amina has already read |50| pages at a rate of |28| pages every |5| days. Gabrielle has read |36| pages and reached |78| pages after |6| days. Let’s assume the reading pace of the 2 friends does not change over the course of the book. Answer the following questions.
Question 1: If the book has |246| pages, who will finish it first?
Question 2: When one friend finishes the book, how many pages will the other friend have left to read?
Begin by finding the rule(s) associated with the reading pace of the 2 friends.
-
Determine the independent variable and the dependent variable
We want to know the number of pages read regarding time, in days.
|x:| time (days)
|y:| number of pages read -
Find the rule
Let's start with Amina's.-
Find parameter |\boldsymbol{a}|
The problem states that she reads |28| pages every |5| days. It is the rate of change.
||a=\dfrac{28}{5}|| -
Find parameter |\boldsymbol{b}|
The initial value represents the number of pages read by the time the friends first got together to discuss the book.
||b=50||
The function rule for Amina is therefore |y_a=\dfrac{28}{5}x+50.|
Next, let’s find the function rule for Gabrielle.
-
Find parameter |\boldsymbol{a}|
The problem states that she had read |36| pages by the time the friends first discussed the book, and after |6| days, she had read |78| pages.
Therefore, find the rate of change using the points |(0,36)| and |(6,78).|
||\begin{align}a&=\dfrac{y_2-y_1}{x_2-x_1}\\&=\dfrac{78-36}{6-0}\\&=\dfrac{42}{6}\\&=7\end{align}|| -
Find parameter |\boldsymbol{b}|
The initial value represents the number of pages read at the time the friends first talked about the book.
||b=36||
The rule for Gabrielle is therefore |y_g=7x+36.|
-
Question 1: If the book has |246| pages, who will finish it first?
We are looking for the number of days it will take each girl to read |246| pages.
-
Replace the given value into the rule
The number of pages is given, so the |y|-value must be replaced in the rule(s) and the corresponding |x|-values must be found.
Amina ||246=\dfrac{28}{5}x+50||
Gabrielle ||246=7x+36||
-
Isolate the other variable
Amina ||\begin{align}246\color{#ec0000}{-50}&=\dfrac{28}{5}x+50\color{#ec0000}{-50}\\196&=\dfrac{28}{5}x\\
196\color{#ec0000}{\times 5}&=\dfrac{28}{5}x\color{#ec0000}{\times 5}\\980&=28x\\\color{#ec0000}{\dfrac{\color{black}{980}}{28}}&=\color{#ec0000}{\dfrac{\color{black}{28x}}{28}}\\35&=x\end{align}||
Gabrielle ||\begin{align}246\color{#ec0000}{-36}&=7x+36\color{#ec0000}{-36}\\210&=7x\\\color{#ec0000}{\dfrac{\color{black}{210}}{7}}&=\color{#ec0000}{\dfrac{\color{black}{7x}}{7}}\\30&=x\end{align}||
-
Answer the question
Gabrielle will finish the book first after |30| days, while Amina will finish it after |35| days.
Question 2: When one friend finishes the book, how many pages will the other friend have left to read?
We need to find the number of pages Amina will have read after |30| days.
-
Replace the given value into the rule
The given data is a number of days, so an |x|-value. So, replace |x| in Amina's rule and find the corresponding |y|-value.
||y_a=\dfrac{28}{5}(30)+50|| -
Isolate the other variable
||\begin{align}y_a&=\dfrac{28}{5}\times30+50\\&=\dfrac{840}{5}+50\\&=168+50\\&=218\end{align}|| -
Answer the question
We are looking for the number of remaining pages, so a subtraction is needed.
||246-218=28||
When Gabrielle finishes reading the book, Amina will have |28| pages left to read.
The following is the graphical representation of the situation.

Pour valider ta compréhension à propos de la résolution de problèmes à l’aide de la fonction affine de façon interactive, consulte la MiniRécup suivante.
