Pour résoudre des problèmes impliquant la fonction cosinus, il faut savoir comment résoudre une équation ou une inéquation trigonométrique et savoir l'appliquer dans un problème avec un contexte réel. Voici un exemple inspiré de la Physique.
On peut modéliser la hauteur d'une masse par rapport au sol grâce à une fonction cosinus. Cette masse est attachée à un ressort.
Voici quelques informations.
-
La hauteur initiale de la masse est de 20 centimètres par rapport au sol.
-
La masse met 10 secondes avant de revenir à sa hauteur initiale.
-
La masse atteint une hauteur minimale de 2 centimètres par rapport au sol.
a) Déterminez l'équation de la fonction cosinus modélisant cette situation.
On doit trouver l'équation sous la forme |y=a \cos(b(x-h))+k.|
On peut tout d'abord calculer l'amplitude puisqu'on connait la hauteur maximale de la masse (c'est sa hauteur) et la hauteur minimale de la masse. ||\text{Amplitude} = \dfrac{\max - \min}{2} = \dfrac{20-2}{2} = 9||Ainsi, on connait la valeur de |a| qui est de |9.| Nous déterminerons son signe plus tard.
On peut maintenant trouver la valeur de |b| en utilisant la période (celle-ci est de 10 secondes).||\text{Période}=\dfrac{2\pi}{\vert b \vert}||Par conséquent, |\vert b \vert = \dfrac{2\pi}{10} = \dfrac{\pi}{5}.|
Le paramètre |h| vaut |0| et le paramètre |k| vaut |20-9=11.|
De plus, comme la fonction est décroissante (la masse est à sa hauteur maximale au départ), alors le |a| doit être positif. On conclut donc que |a=9.|
On peut donc écrire l'équation de la fonction : |y=9 \cos \left(\dfrac{\pi}{5}x \right) + 11.|
On obtient également le graphique suivant.
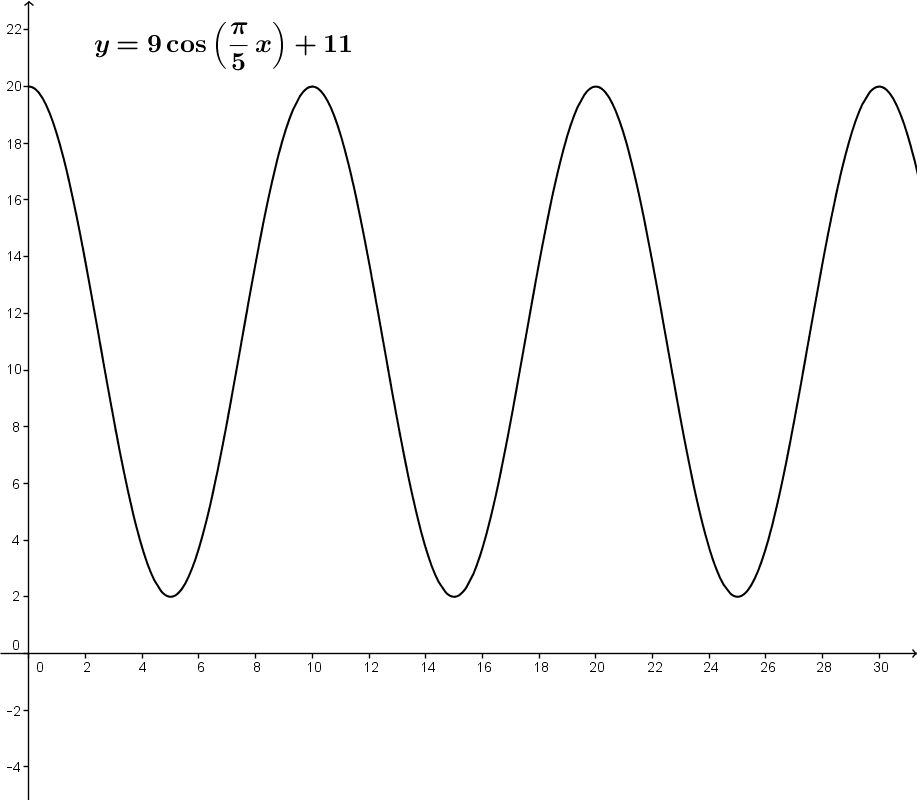
b) Durant 1 minute, pendant combien de temps la masse est-elle à une hauteur supérieure 12 centimètres par rapport au sol?
On doit résoudre l'inéquation |12 < 9\cos\left(\dfrac{\pi}{5}x\right) +11.|
On commence en changeant le signe d'inégalité pour le signe d'égalité. ||\begin{align} 12 &= 9 \cos\left(\dfrac{\pi}{5}x\right)+11\\ 1 &= 9 \cos\left(\dfrac{\pi}{5}x\right)\\ \dfrac{1}{9} &= \cos\left(\dfrac{\pi}{5}x\right)\end{align}||
On doit utiliser la fonction arc cosinus |(\cos^{-1}).|
On obtient alors la valeur de |1{,}459| radians. Par la suite, il faut aller chercher l'autre valeur en faisant |2\pi - 1{,}459 = 4{,}824| radians.
On a donc que l'angle doit être égal à |1{,}459| ou à |4{,}824| radians. Nous voulons les valeurs de |x,| il faut donc isoler |x| dans les 2 équations suivantes : |\dfrac{\pi}{5}x = 1{,}459| et |\dfrac{\pi}{5}x = 4{,}824|
En résolvant ces 2 équations on obtient |x=2{,}323| et |x=7{,}678.|
On doit interpréter ces valeurs.
En regardant le graphique plus haut, on remarque que la masse aura une hauteur supérieure à |12| centimètres de |0| à |2{,}323| secondes et de |7{,}678| à |10| secondes.
Ainsi, la masse est à une hauteur supérieure à |12| centimètres par rapport au sol pendant environ |4{,}645| secondes.
Ceci est pour le 1er cycle. En 1 minute, il s'écoule |6| cycles, car la période est de |10| secondes.
Réponse : |4{,}645 \times 6 = 27{,}87| secondes.