-
Une équation ou une inéquation trigonométrique contient au moins un rapport trigonométrique où l’inconnue |(x)| apparait dans l’argument.
-
Une équation ou une inéquation trigonométrique de degré 2 contient au moins un rapport trigonométrique élevé au carré ou au moins un produit de 2 rapports trigonométriques.
Puisque les fonctions trigonométriques sont des fonctions périodiques, ce type d’équations peut ne posséder aucune solution, ou posséder une solution, plusieurs solutions ou une infinité de solutions.
De plus, il est nécessaire d’utiliser les angles en radians.
Parfois, les équations trigonométriques à résoudre ne contiennent qu’un seul rapport trigonométrique. D’autres fois, elles contiennent plus d’un rapport. Les stratégies à employer pour résoudre ces dernières sont plus variées.
Voici quelques stratégies qu’on peut utiliser lorsqu’on résout une équation ou une inéquation composée de plus d’un rapport trigonométrique.
-
Utiliser les définitions des rapports trigonométriques.
-
Utiliser les identités trigonométriques.
-
Réécrire les fractions à l’aide d’un dénominateur commun.
-
Poser les restrictions.
-
Faire un changement de variable.
-
Utiliser la factorisation ou la formule quadratique.
-
Utiliser le cercle trigonométrique ou les fonctions réciproques |\arcsin,| |\arccos| et |\arctan| pour déterminer les solutions.
-
Calculer la période afin de donner toutes les solutions.
Remarque : Les 3 premières stratégies permettent de réécrire toute l’équation en sinus ou en cosinus seulement, ce qui rend l’équation plus facile à résoudre. Par ailleurs, la plupart du temps, il ne faut pas utiliser toutes ces stratégies et il ne faut pas nécessairement les utiliser dans cet ordre précis.
Voici un rappel des définitions et des identités trigonométriques qui sont souvent utilisées pour résoudre des équations trigonométriques.
Les définitions
||\begin{align}\tan(x)&=\dfrac{\sin(x)}{\cos(x)}\\[3pt]\text{cosec}(x)&=\dfrac{1}{\sin(x)}\\[3pt]\sec(x)&=\dfrac{1}{\cos(x)}\\[3pt]\text{cotan}(x)&=\dfrac{1}{\tan(x)}=\dfrac{\cos(x)}{\sin(x)}\end{align}||
Les identités de base
||\begin{align}\cos(-x)&=\cos(x)\\[3pt] \sin(-x)&=-\sin(x) \end{align}||
Les identités pythagoriciennes
||\begin{alignat}{13}&\cos^2(x)&&+\sin^2(x)&&=1\\[3pt]&\quad\,1&&+\tan^2(x)&&=\sec^2(x)\\[3pt] &\text{cotan}^2(x)&&+\quad1&&=\text{cosec}^2(x)\end{alignat}||
||\begin{align}\sin(A+B)&=\sin(A)\cos(B)+\cos(A)\sin(B)\\[2pt] \sin(A-B)&=\sin(A)\cos(B)-\cos(A)\sin(B)\\[2pt] \sin(2A)&=2\sin(A) \cos(A) \end{align}||
||\begin{align}\cos(A+B)&=\cos(A)\cos(B)-\sin(A)\sin(B)\\[2pt] \cos(A-B)&=\cos(A)\cos(B)+\sin(A)\sin(B)\\[2pt] \cos(2A)&=\cos^2(A)-\sin^2 (A)\end{align}||
||\begin{align}\tan(A+B)&=\dfrac{\tan(A)+\tan(B)}{1-\tan(A)\tan(B)}\\[5pt]\tan(A-B)&=\dfrac{\tan(A)-\tan(B)}{1+\tan(A)\tan(B)} \\[5pt] \tan(2A) &=\dfrac{2 \tan(A)}{1-\tan^2(A)} \end{align}||
Lorsqu’on utilise les fonctions réciproques |\arcsin,| |\arccos| ou |\arctan| sur la calculatrice, on obtient une seule valeur d’angle |(\theta).|
|\boldsymbol\arcsin|
On trouve l’autre angle qui a le même sinus que |\theta| en faisant |\pi - \theta.|
|\boldsymbol\arccos|
On trouve l’autre angle qui a le même cosinus que |\theta| en faisant |- \theta.|
|\boldsymbol\arctan|
Pour la fonction |\arctan,| on n’a pas besoin de trouver l’autre angle, puisque la période d’une fonction tangente est de |\pi| et non de |2\pi.|
Sachant que |\cos(x) = \dfrac{2}{3}| et que |x| est un angle compris entre |0| et |\dfrac{\pi}{2},| quelle est la valeur des expressions suivantes?
a) |\sec(x)|
b) |\sin(x)|
c) |\text{cotan}(x)|
d) |\tan(-x)|
Pour répondre à ces 4 sous-questions, on pourrait avoir tendance à commencer par résoudre l’équation |\cos(x)= \dfrac{2}{3}| afin de trouver la valeur de |x,| puis remplacer cette valeur dans chaque expression. Toutefois, ce n’est pas nécessaire.
a) On sait que |\sec(x)| est l’inverse de |\cos(x).| ||\sec(x)= \dfrac{1}{\cos(x)}||
Pour trouver la valeur de |\sec(x),| il suffit donc de remplacer |\cos(x)| par |\dfrac{2}{3}.|
||\begin{align}\sec(x)&= \dfrac{1}{\cos(x)}\\ &= \dfrac{1}{\frac{\large2}{\large3}}\\ &= \dfrac{3}{2}\end{align}||
b) Pour trouver la valeur de |\sin(x)| à partir de |\cos(x),| on peut utiliser la 1re identité pythagoricienne : |\cos^2(x)+ \sin^2(x)=1.| On remplace |\cos(x)| par sa valeur, soit |\dfrac{2}{3},| puis on isole |\sin(x).|
||\begin{align}\cos^2(x)+ \sin^2(x)&=1\\ \left(\dfrac{2}{3}\right)^{\!2}+\sin^2(x)&=1\\ \dfrac{4}{9}+\sin^2(x)&=1\\ \sin^2(x)&=\dfrac{5}{9}\\ \sin(x)&=\sqrt{\dfrac{5}{9}}\\ \sin(x)&= \pm\dfrac{\sqrt5}{3}\end{align}||Il y a donc 2 solutions possibles pour |\sin(x),| soit |x=\dfrac{\sqrt5}{3}| et |x=-\dfrac{\sqrt5}{3}.| Toutefois, dans l’énoncé, il est précisé que |x| est un angle compris entre |0| et |\dfrac{\pi}{2},| ce qui signifie qu’il se situe dans le 1er quadrant du cercle trigonométrique. Dans ce quadrant, les rapports trigonométriques sont positifs. La solution est donc |\sin(x)=\dfrac{\sqrt5}{3}.|
c) Pour trouver la valeur de |\text{cotan}(x),| on utilise la définition : |\text{cotan}(x)= \dfrac{\cos(x)}{\sin(x)}.| Il suffit de remplacer |\cos(x)| par |\dfrac{2}{3}| et |\sin(x)| par |\dfrac{\sqrt5}{3},| qu’on vient de calculer.
||\begin{align}\text{cotan}(x) &= \dfrac{\cos(x)}{\sin(x)}\\ &=\dfrac{\dfrac{2}{3}}{\dfrac{\sqrt5}{3}}\\&=\dfrac{2}{3}\times \dfrac{3}{\sqrt5}\\ &=\dfrac{2}{\sqrt5}\end{align}||Finalement, pour donner une solution qui respecte les normes mathématiques, il faut rationaliser la fraction.||\begin{align}\text{cotan}(x)&=\dfrac{2\ \boldsymbol{\color{#3a9a38}{(\sqrt{5})}}}{\sqrt{5}\ \boldsymbol{\color{#3a9a38}{(\sqrt{5})}}}\\&=\dfrac{2\sqrt{5}}{5}\end{align}||
d) Pour trouver la valeur de |\tan(-x),| on utilise la définition |\tan(-x)= \dfrac{\sin(-x)}{\cos(-x)}.|
Ensuite, on utilise les identités trigonométriques de base |\cos(-x)=\cos(x)| et |\sin(-x)=-\sin(x).|
||\begin{align}\tan(-x) &= \dfrac{\sin(-x)}{\cos(-x)}\\[3pt] &=\dfrac{-\sin(x)}{\cos(x)}\end{align}||Maintenant, on remplace |\cos(x)| par |\dfrac{2}{3}| et |\sin(x)| par |\dfrac{\sqrt5}{3},| qu’on a calculés à la sous-question b).||\begin{align}\tan(-x)&=\dfrac{-\sin(x)}{\cos(x)}\\[3pt]&=\dfrac{-\dfrac{\sqrt5}{3}}{\dfrac{2}{3}}\\[3pt]&=-\dfrac{\sqrt5}{3}\times\dfrac{3}{2}\\[3pt]&=-\dfrac{\sqrt5}{2}\end{align}||
Résous l'équation suivante.||\tan^2(x)-3\sec(x)\tan(x)-\sec^2(x)=-1||
-
Utiliser les identités trigonométriques pythagoriciennes
En utilisant l’identité |1+\tan^2(x)=\sec^2(x),| il est possible de remplacer |\tan^2(x)| par |\sec^2(x)-1.|
||\begin{align}\boldsymbol{\color{#3b87cd}{\tan^2(x)}}-3\sec(x)\tan(x)-\sec^2(x)&=-1\\[3pt] \boldsymbol{\color{#3b87cd}{\sec^2(x)-1}}-3\sec(x)\tan(x)-\sec^2(x)&=-1\\[3pt] -3\sec(x)\tan(x)&=0\\[3pt] \sec(x)\tan(x)&=0 \end{align}||
-
Utiliser les définitions des rapports trigonométriques
Cela permet de réécrire toute l’équation en sinus et en cosinus.||\begin{align}\sec(x)\tan(x)&=0\\ \dfrac{1}{\cos(x)} \dfrac{\sin(x)}{\cos(x)}&=0\\ \dfrac{\sin(x)}{\cos^2(x)}&=0 \end{align}|| -
Poser les restrictions
Dès qu’il y a des fractions, il faut s’assurer que chaque dénominateur soit différent de |0.| ||\begin{alignat}{1} \cos^2(&x)&&\ne 0\\ &\!\!\Downarrow\\ \cos(&x)&&\ne 0\\ &\!\!\Downarrow\\[-20pt] &x &&\ne \left\lbrace\dots,\dfrac{\pi}{2},\dfrac{3\pi}{2},\dots\right\rbrace \end{alignat}|| -
Utiliser le cercle trigonométrique pour déterminer les solutions
Pour que la fraction |\dfrac{\sin(x)}{\cos^2(x)}| soit égale à |0,| il suffit que le numérateur soit nul. Or, en observant le cercle trigonométrique, on sait que |\sin(x)=0| si |x\in\{\dots,\,0,\,\pi,\,2\pi\dots\}.| Ces valeurs respectent les restrictions.
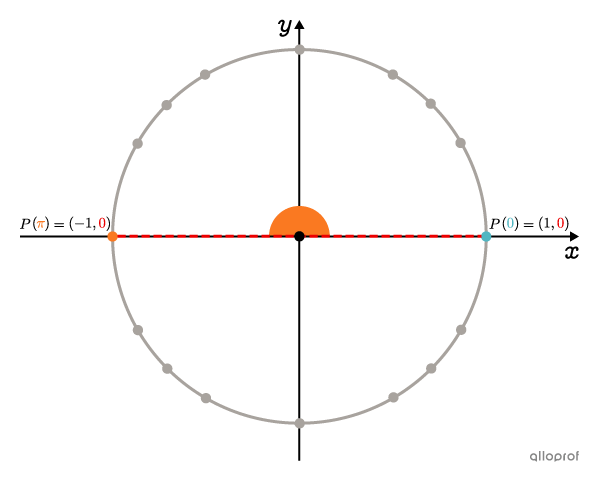
Réponse : Les solutions de l’équation |\tan^2(x)-3\sec(x)\tan(x)-\sec^2(x)=-1| sont les suivantes. ||x\in\{\dots,\,0,\,\pi,\,2\pi\dots\}||
Remarque : On a commencé par les identités pythagoriciennes au lieu des définitions des rapports trigonométriques, mais faire le contraire aurait très bien fonctionné.
Résous l'équation suivante.||2\sin^2(x)+\cos(2x)+1=0||
-
Utiliser les identités trigonométriques d’une somme ou d’une différence
On utilise d’abord l’identité |\cos(2A)=\cos^2(A)-\sin^2 (A).|
||\begin{align}2\sin^2(x)+\boldsymbol{\color{#3b87cd}{\cos(2x)}}+1&=0\\ 2\sin^2(x)+\boldsymbol{\color{#3b87cd}{\cos^2(x)-\sin^2(x)}}+1&=0\\ \sin^2(x)+\cos^2(x)+1&=0\end{align}||
-
Utiliser les identités trigonométriques pythagoriciennes||\begin{align}\boldsymbol{\color{#3b87cd}{\sin^2(x)+\cos^2(x)}}+1&=0\\ \boldsymbol{\color{#3b87cd}{1}}+1&=0\\ 2&=0\end{align}||On obtient une égalité qui est fausse. Cela signifie que l’équation de départ n’a pas de solutions.
Réponse : L’équation |2\sin^2(x)+\cos(2x)+1=0| n’a pas de solutions.
Remarque : Quand on obtient plutôt une égalité évidente comme |0=0,| cela signifie que l’équation a une infinité de solutions, c’est-à-dire que n’importe quelle valeur réelle de |x| est une solution de l’équation de départ.
On utilise aussi les identités trigonométriques d’une somme ou d’une différence pour calculer la valeur exacte d’un rapport trigonométrique.
Résous l'équation suivante.||\sin(x)\cos(x)=2\cos(x)||
-
Utiliser la factorisation afin de ramener l’équation sous la forme d’un produit de facteurs égal à |\boldsymbol{0}|
On soustrait |2 \cos(x)| de chaque côté de l'égalité.||\sin(x)\cos(x) - 2\cos(x)= 0||On effectue une mise en évidence simple de |\cos(x).| ||\cos(x)\Big(\!\sin(x) - 2\Big) =0||Attention! On pourrait avoir le réflexe de diviser les 2 côtés de l’équation par |\cos(x)| afin de la simplifier, mais c’est à éviter. En effet, cela changerait le degré de l’équation, ce qui aurait pour conséquence d’éliminer des solutions. -
Appliquer la règle du produit nul
Le produit est égal à |0| si |\cos(x)=0| ou si |\sin(x)-2=0.| On se retrouve donc avec 2 équations à résoudre.
|\boldsymbol{\cos(x)=0}|
Puisque |\boldsymbol{\color{#333fb1}{0}}| est une abscisse de points remarquables, on détermine les angles recherchés directement à partir du cercle trigonométrique.

On trouve que les angles pour lesquels l’abscisse vaut |\boldsymbol{\color{#333fb1}{0}}| sont |\boldsymbol{\color{#fa7921}{\dfrac{\pi}{2}}}| et |\boldsymbol{\color{#51b6c2}{\dfrac{3\pi}{2}}}.|
La période de la fonction cosinus étant de |2\pi,| les solutions de l’équation |\cos(x)=0| sont |x\in \left\lbrace \dfrac{\pi}{2} + 2\pi n,\ \dfrac{3\pi}{2} + 2 \pi n \right\rbrace| où |n\in\mathbb{Z}.|
|\boldsymbol{\sin(x)-2=0}|
On isole le rapport sinus.||\begin{align}\sin(x)-2&=0\\ \sin(x) &=2\end{align}||Cette équation n’a aucune solution, car le sinus d’un angle est toujours compris entre |-1| et |1| inclusivement. Or, |2\not\in[-1,1].|
Réponse : Les solutions de l’équation |\sin(x)\cos(x)=2\cos(x)| sont les suivantes.
||x\in\left\lbrace \dfrac{\pi}{2} + 2\pi n,\ \dfrac{3\pi}{2} + 2 \pi n \right\rbrace||où |n\in\mathbb{Z}|
Résous l'équation suivante.||15\sin(x)\cos(x)-2=5\sin(x)-6\cos(x)||
-
Utiliser la factorisation afin de ramener l’équation sous la forme d’un produit de facteurs égal à |\boldsymbol{0}|
On rapporte les termes du même côté de l’égalité.
||\begin{align}15\sin(x)\cos(x)-2&=5\sin(x)-6\cos(x)\\15\sin(x)\cos(x)-5\sin(x)+6\cos(x)-2&=0\end{align}||
On effectue une mise en évidence double.
||\begin{align}15\sin(x)\cos(x)-5\sin(x)+6\cos(x)-2&=0\\ 5\sin(x)\big(3\cos(x)-1\big)+2\big(3\cos(x)-1\big)&=0\\ \big(3\cos(x)-1\big)\big(5\sin(x)+2\big)&=0\end{align}||
-
Appliquer la règle du produit nul
Le produit est égal à |0| si l’un ou l’autre des 2 facteurs est égal à |0.| On se retrouve donc avec 2 équations à résoudre.
|\boldsymbol{3\cos(x)-1=0}|
On isole le rapport cosinus.||\begin{align} 3\cos(x)-1&=0\\ 3\cos(x)&=1\\ \cos(x)&=\dfrac{1}{3} \end{align}||On trouve la 1re valeur de |x| en utilisant |\arccos,| puis la 2e valeur est son opposé.||\begin{align}\cos(x)&=\dfrac{1}{3}\\x&=\arccos\left(\dfrac{1}{3}\right)\\ x_1&\approx1{,}23\quad\text{et}\quad x_2\approx-1{,}23 \end{align}||La période de la fonction |y=3\cos(x)-1| étant de |2\pi,| les solutions de l’équation |3\cos(x)-1=0| sont |x\in \left\lbrace -1{,}23 + 2\pi n;\ 1{,}23 + 2 \pi n \right\rbrace| où |n\in\mathbb{Z}.|
|\boldsymbol{5\sin(x)+2=0}|
On isole le rapport sinus.||\begin{align}5\sin(x)+2&=0\\ 5\sin(x)&=-2\\ \sin(x)&=\dfrac{-2}{5}\end{align}||On trouve la 1re valeur de |x| en utilisant |\arcsin,| puis on obtient la 2e valeur en soustrayant |x_1| à |\pi.| ||\begin{align}\sin(x)&=\dfrac{-2}{5}\\ x&=\arcsin\left(\dfrac{-2}{5}\right)\end{align}|| ||\begin{aligned}x_1\approx -0{,}41\quad\text{et}\\\\ \end{aligned} \quad \begin{aligned}x_2&\approx\pi--0{,}41\\ &\approx3{,}55 \end{aligned}||La période de la fonction |y=5\sin(x)+2| étant de |2\pi,| les solutions de l’équation |5\sin(x)+2=0| sont |x\in \left\lbrace -0{,}41 + 2\pi n;\ 3{,}55 + 2 \pi n \right\rbrace| où |n\in\mathbb{Z}.|
Réponse : Les solutions de l’équation |15\sin(x)\cos(x)-2=5\sin(x)-6\cos(x)| sont les suivantes.
||x\in\left\lbrace -1{,}23+2\pi n;\, -0{,}41+2\pi n;\, 1{,}23+2\pi n;\, 3{,}55+2\pi n\right\rbrace||où |n\in\mathbb{Z}|
Résous l'équation suivante.||3\tan(x)+\text{cotan}(x)=5\,\text{cosec}(x)||
Résous l'équation suivante.||3\tan(x)+\text{cotan}(x)=5\,\text{cosec}(x)||
-
Utiliser les définitions des rapports trigonométriques
Cela permet de réécrire toute l’équation en sinus et en cosinus.||\begin{alignat}{13} 3\tan(x)&+\text{cotan}(x)&&=5\text{ cosec}(x)\\[3pt] 3\dfrac{\sin(x)}{\cos(x)}&+\dfrac{\cos(x)}{\sin(x)}&&=\dfrac{5}{\sin(x)} \end{alignat}||
-
Poser les restrictions
Dès qu’il y a des fractions, il faut s’assurer que chaque dénominateur soit différent de |0.|
||\begin{alignat}{13} \cos&(x)&&\ne0\\[3pt]&\,\Downarrow\\ &\ \ x&&\ne\left\{\dots,\dfrac{\pi}{2},\dfrac{3\pi}{2},\dots\right\}\end{alignat}||
||\begin{alignat}{13}\sin&(x)&&\ne0\\&\,\Downarrow\\&\ \ x&&\ne\{\dots, 0,\,\pi,\,2\pi,\dots\}\end{alignat}||
En résumé, |x| doit être différent de |\left\{\dots,\,0,\,\dfrac{\pi}{2},\,\pi,\,\dfrac{3\pi}{2},\,2\pi,\,\dots\right\}.|
-
Réécrire les fractions à l’aide d’un dénominateur commun
Pour trouver le dénominateur commun, on peut multiplier les dénominateurs ensemble. Ainsi, le dénominateur commun est |\cos(x)\sin(x).| Il faut donc multiplier la 1re fraction par |\dfrac{\sin(x)}{\sin(x)}| et les 2 autres par |\dfrac{\cos(x)}{\cos(x)}.|
||\begin{align}\dfrac{3\sin(x)}{\cos(x)}+\dfrac{\cos(x)}{\sin(x)}&=\dfrac{5}{\sin(x)}\\[3pt]\dfrac{3\sin(x)}{\cos(x)}\times\dfrac{\sin(x)}{\sin(x)}+\dfrac{\cos(x)}{\sin(x)}\times\dfrac{\cos(x)}{\cos(x)}&=\dfrac{5}{\sin(x)}\times\dfrac{\cos(x)}{\cos(x)}\\[3pt]\dfrac{3\sin^2(x)}{\cos(x)\sin(x)}+\dfrac{\cos^2(x)}{\cos(x)\sin(x)}&=\dfrac{5\cos(x)}{\cos(x)\sin(x)}\end{align}||
En multipliant les 2 côtés de l'égalité précédente par |\cos(x)\sin(x),| on obtient l’équation suivante. ||3\sin^2(x) + \cos^2(x) = 5\cos(x)||
-
Utiliser les identités trigonométriques pythagoriciennes
En utilisant l’identité |\cos^2(x) + \sin^2(x)=1,| il est possible de remplacer |\sin^2(x)| par |1-\cos^2(x).| ||\begin{align} 3\boldsymbol{\color{#3b87cd}{\sin^2(x)}}+ \cos^2(x) &= 5\cos(x)\\ 3\!\boldsymbol{\color{#3b87cd}{\left(1-\cos^2 (x)\right)}} + \cos^2(x) &= 5\cos(x)\end{align}||Il reste à simplifier l’équation et à rapporter tous les termes du même côté de l’égalité.||\begin{align} 3-3\cos^2 (x) + \cos^2(x) &= 5\cos(x) \\3-2\cos^2 (x)&=5\cos(x)\\3-2\cos^2(x) -5\cos(x)&=0\end{align}||
-
Faire un changement de variable
En posant |\cos(x)= z,| on obtient |-2z^2 -5z + 3=0.| On laisse donc temporairement de côté les rapports cosinus afin de se concentrer sur la résolution de l’équation de degré 2.
-
Utiliser la factorisation et appliquer la règle du produit nul
Il faut factoriser le trinôme |-2z^2 -5z + 3.| On peut appliquer la technique du produit-somme.
On cherche donc 2 nombres dont le produit est égal à |-2\times 3=-6| et dont la somme est égale à |-5.| Ces 2 nombres sont |1| et |-6.|
On réécrit le trinôme en décomposant le terme |-5z.| ||-2z^2 \boldsymbol{\color{#3b87cd}{-5z}} + 3\\-2z^2\boldsymbol{\color{#3b87cd}{+1z-6z}}+3||On effectue la mise en évidence double.||-2z^2+1z-6z+3\\ z(-2z+1)+3(-2z+1)\\(-2z+1)(z+3)||On applique la règle du produit nul. Cette expression algébrique est égale à |0| si |-2z+1=0| ou si |z+3=0.| ||\begin{align}\begin{aligned}-2z+1&=0\\-2z&=-1\\ z_1&=\dfrac{1}{2}\end{aligned}\qquad \begin{aligned}z+3&=0\\ z_2&=-3 \\ \phantom{\dfrac{1}{2}} \end{aligned}\end{align}||Les solutions de l’équation |-2z^2-5z+3=0| sont donc |z_1=\dfrac{1}{2}| et |z_2=-3.| Puisqu’on a fait un changement de variable, on peut substituer |z| par |\cos(x).| On obtient alors 2 nouvelles équations : |\cos(x)=\dfrac{1}{2}| et |\cos(x)=-3.|
L’équation |\cos(x)=-3| n’a aucune solution, car le cosinus d’un angle doit toujours être compris entre |-1| et |1| inclusivement. Or, |-3\not\in[-1,1].|
Ainsi, il ne reste que l’équation |\cos(x) = \dfrac{1}{2}| à résoudre.
-
Utiliser le cercle trigonométrique pour déterminer les solutions
Puisque |\boldsymbol{\color{#333fb1}{\dfrac{1}{2}}}| est une abscisse de points remarquables, on détermine les angles recherchés directement à partir du cercle trigonométrique.
On trouve que les angles pour lesquels l’abscisse vaut |\boldsymbol{\color{#333fb1}{\dfrac{1}{2}}}| sont |\boldsymbol{\color{#fa7921}{\dfrac{\pi}{3}}}| et |\boldsymbol{\color{#51b6c2}{\dfrac{5\pi}{3}}}.| Ainsi, |x = \dfrac{\pi}{3}| ou |x=\dfrac{5\pi}{3}.| Ces 2 valeurs respectent les restrictions.
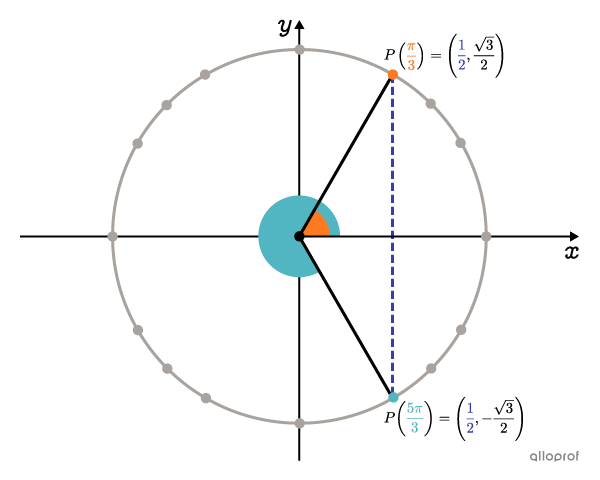
-
Calculer la période et donner les solutions
Comme on a trouvé nos angles trigonométriques à partir d’une fonction cosinus avec |b=1,| on utilise la période de base des fonctions sinusoïdales qui est de |2\pi.|
Réponse : Les solutions de l’équation |3\tan(x)+\text{cotan}(x)=5\,\text{cosec}(x)| sont les suivantes.
|x\in\left\lbrace \dfrac{\pi}{3} + 2\pi n, \dfrac{5\pi}{3} + 2\pi n \right\rbrace| où |n\in\mathbb{Z}|
Pour résoudre une inéquation trigonométrique, on utilise les mêmes stratégies que pour résoudre une équation trigonométrique. Puis, lorsqu’on a les solutions de l’équation, on trouve l’ensemble-solution de l’inéquation en testant des valeurs situées de part et d’autre des solutions trouvées.
De plus, il faut toujours porter une attention particulière aux bornes des intervalles de notre ensemble-solution.
-
Si le signe d’inéquation est |<| ou |>,| les bornes sont exclues.
-
Si le signe d’inéquation est |\leq| ou |\geq,| les bornes sont incluses.
-
Lorsqu’une borne correspond à une asymptote (pour la fonction tangente), elle est toujours exclue.
Résous l'inéquation suivante.||2\tan(x)+4\sec(x)\le 3\sin(x)+6||
-
Changer le symbole d’inégalité par un symbole d’égalité
||\begin{align}2\tan(x)+4\sec(x)&\le 3\sin(x)+6\\ &\downarrow\\ 2\tan(x)+4\sec(x)&= 3\sin(x)+6\end{align}||
-
Utiliser les définitions des rapports trigonométriques
Cela permet de réécrire toute l’équation en sinus et en cosinus.||\begin{align} 2\dfrac{\sin(x)}{\cos(x)}+4\dfrac{1}{\cos(x)}&= 3\sin(x)+6\\[3pt]\dfrac{2\sin(x)+4}{\cos(x)}&= 3\sin(x)+6\end{align}||
-
Poser les restrictions
Dès qu’il y a des fractions, il faut s’assurer que chaque dénominateur soit différent de |0.| ||\begin{alignat}{13} \cos&(x)&&\ne0\\[3pt]&\,\Downarrow\\ &\ \ x&&\ne\left\{\dots,\dfrac{\pi}{2},\dfrac{3\pi}{2},\dots\right\}\end{alignat}||
-
Utiliser la factorisation afin de ramener l’équation sous la forme d’un produit de facteurs égal à |\boldsymbol{0}|
On multiplie les 2 côtés de l’égalité par |\cos(x).| On obtient l’équation suivante.||2\sin(x)+4= 3\sin(x)\cos(x)+6\cos(x)||On soustrait |2\sin(x)+4| des 2 côtés.||0= 3\sin(x)\cos(x)+6\cos(x)-2\sin(x)-4||On fait une mise en évidence double.||\begin{align}0&= 3\sin(x)\cos(x)+6\cos(x)-2\sin(x)-4\\ 0&= 3\cos(x)\big(\!\sin(x)+2\big)-2\big(\!\sin(x)+2\big)\\ 0&=\big(\!\sin(x)+2\big)\big(3\cos(x)-2\big)\end{align}||
-
Appliquer la règle du produit nul
Le produit est égal à |0| si |\sin(x)+2=0| ou si |3\cos(x)-2=0.| On se retrouve donc avec 2 équations à résoudre.
|\boldsymbol{\sin(x)+2=0}|
On isole le rapport sinus.||\begin{align}\sin(x)+2&=0\\ \sin(x) &=-2\end{align}||Cette équation n’a aucune solution, car le sinus d’un angle est toujours compris entre |-1| et |1| inclusivement. Or, |-2\not\in[-1,1].|
|\boldsymbol{3\cos(x)-2=0}|
On isole le rapport cosinus.||\begin{align} 3\cos(x)-2&=0\\ 3\cos(x)&=2\\ \cos(x)&=\dfrac{2}{3} \end{align}||On trouve la 1re valeur de |x| en utilisant |\arccos,| puis la 2e valeur est son opposé.||\begin{align}\cos(x)&=\dfrac{2}{3}\\x&=\arccos\left(\dfrac{2}{3}\right)\\ x_1&\approx 0{,}84\quad\text{et}\quad x_2\approx-0{,}84 \end{align}||La période de la fonction |y=3\cos(x)-2| étant de |2\pi,| les solutions de l’équation |3\cos(x)-2=0| sont |x\in \left\lbrace -0{,}84 + 2\pi n;\ 0{,}84 + 2 \pi n \right\rbrace| où |n\in\mathbb{Z}.|
-
Donner l’ensemble-solution de l’inéquation
Pour déterminer les intervalles qui font partie de l’ensemble-solution, on place les solutions de l’équation qu’on a trouvées à l’étape 5 de même que les restrictions qu’on a trouvées à l’étape 3 sur une droite numérique.
En ordre croissant, on a d’abord la valeur |x_2=-0{,}84.| Ensuite, on a la valeur |x_1=0{,}84.| Puis, on a une restriction à |x=\dfrac{\pi}{2}\approx 1{,}57| et une autre à |x=\dfrac{3\pi}{2}\approx 4{,}71.| Enfin, on retrouve une valeur équivalente à |x_2,| mais une période plus loin : |x_3\approx -0{,}84+2\pi\approx 5{,}44.|

Il y a donc 4 intervalles possibles, soit celui entre |-0{,}84| et |0{,}84,| celui entre |0{,}84| et |\dfrac{\pi}{2},| celui entre |\dfrac{\pi}{2}| et |\dfrac{3\pi}{2},| et celui entre |\dfrac{3\pi}{2}| et |5{,}44.| Pour déterminer les intervalles qui font partie de l’ensemble-solution, on peut tester une valeur de |x| dans chaque intervalle.
Remarque : Puisque le signe d'inégalité est |\le,| les bornes de l’intervalle sont incluses dans l’ensemble-solution. Par contre, les restrictions ne le sont pas.
||\left[\boldsymbol{\color{#51b6c2}{-0{,}84}};\ \boldsymbol{\color{#fa7921}{0{,}84}}\right]||
On teste |x=0.| ||\begin{align}2\tan(x)+4\sec(x)&\le 3\sin(x)+6\\[3pt] 2\tan(x)+\dfrac{4}{\cos(x)}&\le 3\sin(x)+6\\[3pt] 2\tan(0)+\dfrac{4}{\cos(0)}&\overset{\text{?}}{\le} 3\sin(0)+6\\[3pt] 2\times 0+\dfrac{4}{1}&\overset{\text{?}}{\le} 3\times 0+6\\[3pt] 4&\color{#3a9a38}{\le}6\end{align}||Cette inégalité est vraie, ce qui implique que l’intervalle |\left[\boldsymbol{\color{#51b6c2}{-0{,}84}};\ \boldsymbol{\color{#fa7921}{0{,}84}}\right]| fait partie de l’ensemble-solution.
||\left[\boldsymbol{\color{#fa7921}{0{,}84}};\ \boldsymbol{\color{#ec0000}{\dfrac{\pi}{2}}}\right[||
On teste |x=1.| ||\begin{align}2\tan(x)+4\sec(x)&\le 3\sin(x)+6\\[3pt] 2\tan(x)+\dfrac{4}{\cos(x)}&\le 3\sin(x)+6\\[3pt] 2\tan(1)+\dfrac{4}{\cos(1)}&\overset{\text{?}}{\le} 3\sin(1)+6\\[3pt] 2\times 1{,}56+\dfrac{4}{0{,}54}&\overset{\text{?}}{\le} 3\times 0{,}84+6\\[3pt] 10{,}52&\color{#ec0000}{\not\le}8{,}52\end{align}||Cette inégalité est fausse, ce qui implique que l’intervalle |\left[\boldsymbol{\color{#fa7921}{0{,}84}};\ \boldsymbol{\color{#ec0000}{\dfrac{\pi}{2}}}\right[| ne fait pas partie de l’ensemble-solution.
||\left]\boldsymbol{\color{#ec0000}{\dfrac{\pi}{2}}},\boldsymbol{\color{#ec0000}{\dfrac{3\pi}{2}}}\right[||
On teste |x=\pi.| ||\begin{align}2\tan(x)+4\sec(x)&\le 3\sin(x)+6\\[3pt] 2\tan(x)+\dfrac{4}{\cos(x)}&\le 3\sin(x)+6\\[3pt] 2\tan(\pi)+\dfrac{4}{\cos(\pi)}&\overset{\text{?}}{\le} 3\sin(\pi)+6\\[3pt] 2\times 0+\dfrac{4}{-1}&\overset{\text{?}}{\le} 3\times 0+6\\[3pt] -4&\color{#3a9a38}{\le}6\end{align}||Cette inégalité est vraie, ce qui implique que l’intervalle |\left]\boldsymbol{\color{#ec0000}{\dfrac{\pi}{2}}},\boldsymbol{\color{#ec0000}{\dfrac{3\pi}{2}}}\right[| fait partie de l’ensemble-solution.
||\left]\boldsymbol{\color{#ec0000}{\dfrac{3\pi}{2}}},\ \boldsymbol{\color{#51b6c2}{5{,}44}}\right]||
On teste |x=5.| ||\begin{align}2\tan(x)+4\sec(x)&\le 3\sin(x)+6\\[3pt] 2\tan(x)+\dfrac{4}{\cos(x)}&\le 3\sin(x)+6\\[3pt] 2\tan(5)+\dfrac{4}{\cos(5)}&\overset{\text{?}}{\le} 3\sin(5)+6\\[3pt] 7{,}34&\color{#ec0000}{\not\le}3{,}12\end{align}||Cette inégalité est fausse, ce qui implique que l’intervalle |\left]\boldsymbol{\color{#ec0000}{\dfrac{3\pi}{2}}},\ \boldsymbol{\color{#51b6c2}{5{,}44}}\right]| ne fait pas partie de l’ensemble-solution.
Réponse : Puisque les bornes des intervalles se répètent à chaque période |(2\pi),| l’ensemble-solution de l’inéquation |2\tan(x)+4\sec(x)\le 3\sin(x)+6| est le suivant.
||x\in\Big[-0{,}84+2\pi n;\ 0{,}84+2\pi n\Big]\ \cup\ \left]\dfrac{\pi}{2}+2\pi n,\dfrac{3\pi}{2}+2\pi n\right[||où |n\in\mathbb{Z}|
Résous l'inéquation suivante.||2\cos^2(x)<1-\sin(x)||
-
Changer le symbole d’inégalité par un symbole d’égalité
||\begin{align}2\cos^2(x)&<1-\sin(x)\\ &\downarrow\\ 2\cos^2(x)&=1-\sin(x)\end{align}||
-
Utiliser les identités trigonométriques pythagoriciennes
En utilisant l’identité |\cos^2(x) + \sin^2(x)=1,| il est possible de remplacer |\cos^2(x)| par |1-\sin^2(x).| ||\begin{align}2\boldsymbol{\color{#3b87cd}{\cos^2(x)}}&=1-\sin(x)\\2\left(\boldsymbol{\color{#3b87cd}{1-\sin^2(x)}}\right)&=1-\sin(x)\\ 2-2\sin^2(x)&=1-\sin(x)\\ 0&=2\sin^2(x)-\sin(x)-1\end{align}||
-
Faire un changement de variable
En posant |\sin(x)= z,| on obtient |2z^2 -z -1=0.| On laisse donc temporairement de côté les rapports sinus afin de se concentrer sur la résolution de l’équation de degré 2.
-
Utiliser la factorisation et appliquer la règle du produit nul
Il faut factoriser le trinôme |2z^2 -z -1.| On peut appliquer la technique du produit-somme. On cherche donc 2 nombres dont le produit est égal à |2\times -1=-2| et dont la somme est égale à |-1.| Ces 2 nombres sont |1| et |-2.|
On réécrit le trinôme en décomposant le terme |-z.| ||2z^2 \boldsymbol{\color{#3b87cd}{-z}}-1\\ 2z^2\boldsymbol{\color{#3b87cd}{-2z+z}}-1||On effectue la mise en évidence double.||2z^2-2z+z-1\\2z(z-1)+1(z-1)\\(z-1)(2z+1)||On applique la règle du produit nul. Cette expression algébrique est égale à |0| si |z-1=0| ou si |2z+1=0.| ||\begin{align}\begin{aligned}z-1&=0\\z_1&=1\\ \phantom{\dfrac{1}{2}}\end{aligned}\qquad \begin{aligned}2z+1&=0\\ 2z&=-1\\ z_2&=-\dfrac{1}{2} \end{aligned}\end{align}||Les solutions de l’équation |2z^2-z-1=0| sont donc |z_1=1| et |z_2=-\dfrac{1}{2}.| Puisqu’on a fait un changement de variable, on peut substituer |z| par |\sin(x).| On obtient alors 2 nouvelles équations : |\sin(x)=1| et |\sin(x)=-\dfrac{1}{2}.|
-
Utiliser le cercle trigonométrique pour déterminer les solutions
Puisque |\boldsymbol{\color{#ec0000}{1}}| et |\boldsymbol{\color{#ec0000}{-\dfrac{1}{2}}}| sont des ordonnées de points remarquables, on détermine les angles recherchés directement à partir du cercle trigonométrique.
On trouve que l’angle pour lequel l’ordonnée vaut |\boldsymbol{\color{#ec0000}{1}}| est |\boldsymbol{\color{#ff55c3}{\dfrac{\pi}{2}}},| tandis que les angles pour lesquels l’ordonnée vaut |\boldsymbol{\color{#ec0000}{-\dfrac{1}{2}}}| sont |\boldsymbol{\color{#fa7921}{\dfrac{7\pi}{6}}}| et |\boldsymbol{\color{#51b6c2}{\dfrac{11\pi}{6}}}.|
Ainsi, |x_1 = \dfrac{\pi}{2},| |x_2=\dfrac{7\pi}{6}| et |x_3=\dfrac{11\pi}{6}.|

-
Donner l’ensemble-solution de l’inéquation
Il y a 3 intervalles possibles, soit celui entre |\boldsymbol{\color{#ff55c3}{\dfrac{\pi}{2}}}| et |\boldsymbol{\color{#fa7921}{\dfrac{7\pi}{6}}},| celui entre |\boldsymbol{\color{#fa7921}{\dfrac{7\pi}{6}}}| et |\boldsymbol{\color{#51b6c2}{\dfrac{11\pi}{6}}},| et celui entre |\boldsymbol{\color{#51b6c2}{\dfrac{11\pi}{6}}}| et la valeur qui est une période plus loin que |\boldsymbol{\color{#ff55c3}{\dfrac{\pi}{2}}}.| Pour déterminer les intervalles qui font partie de l’ensemble-solution, on peut utiliser le graphique ou tester une valeur de |x| dans chaque intervalle.
Remarque : Puisque le signe d'inégalité est |<,| les bornes de l’intervalle ne sont pas incluses dans l’ensemble-solution.
||\left]\boldsymbol{\color{#ff55c3}{\dfrac{\pi}{2}}},\boldsymbol{\color{#fa7921}{\dfrac{7\pi}{6}}}\right[||
On teste |x=\pi.| ||\begin{align}2\cos^2(x)&<1-\sin(x)\\[3pt] 2\cos^2(\pi)&\overset{\text{?}}{<}1-\sin(\pi)\\[3pt] 2(-1)^2&\overset{\text{?}}{<}1-0\\[3pt] 2&\color{#ec0000}{\not<}1\end{align}||Cette inégalité est fausse, ce qui implique que l’intervalle |\left]\boldsymbol{\color{#ff55c3}{\dfrac{\pi}{2}}},\boldsymbol{\color{#fa7921}{\dfrac{7\pi}{6}}}\right[| ne fait pas partie de l’ensemble-solution.
||\left]\boldsymbol{\color{#fa7921}{\dfrac{7\pi}{6}}}, \boldsymbol{\color{#51b6c2}{\dfrac{11\pi}{6}}}\right[||
On teste |x=\dfrac{3\pi}{2}.| ||\begin{align}2\cos^2(x)&<1-\sin(x)\\[3pt] 2\cos^2\left(\dfrac{3\pi}{2}\right)&\overset{\text{?}}{<}1-\sin\left(\dfrac{3\pi}{2}\right)\\2(0)^2&\overset{\text{?}}{<}1--1\\[3pt] 0&\color{#3a9a38}{<}2\end{align}||Cette inégalité est vraie, ce qui implique que l’intervalle |\left]\boldsymbol{\color{#fa7921}{\dfrac{7\pi}{6}}}, \boldsymbol{\color{#51b6c2}{\dfrac{11\pi}{6}}}\right[| fait partie de l’ensemble-solution.
||\begin{align}\left]\boldsymbol{\color{#51b6c2}{\dfrac{11\pi}{6}}},\color{#ff55c3}{\dfrac{\pi}{2}}+p\right[&= \left]\boldsymbol{\color{#51b6c2}{\dfrac{11\pi}{6}}},\color{#ff55c3}{\dfrac{\pi}{2}}+2\pi\right[\\[3pt]&=\left]\boldsymbol{\color{#51b6c2}{\dfrac{11\pi}{6}}},\color{#ff55c3}{\dfrac{5\pi}{2}}\right[\end{align}||
On teste |x=2\pi.| ||\begin{align}2\cos^2(x)&<1-\sin(x)\\[3pt] 2\cos^2(2\pi)&\overset{\text{?}}{<}1-\sin(2\pi)\\[3pt] 2(1)^2&\overset{\text{?}}{<}1-0\\[3pt] 2&\color{#ec0000}{\not<}1\end{align}||Cette inégalité est fausse, ce qui implique que l’intervalle |\left]\boldsymbol{\color{#51b6c2}{\dfrac{11\pi}{6}},\color{#ff55c3}{\dfrac{5\pi}{2}}}\right[| ne fait pas partie de l’ensemble-solution.
Réponse : Puisque les bornes des intervalles se répètent à chaque période |(2\pi),| l’ensemble-solution de l’inéquation |2\cos^2(x)<1-\sin(x)| est le suivant.
||x\in \left]\dfrac{7\pi}{6}+2\pi n,\dfrac{11\pi}{6}+2\pi n\right[||où |n\in\mathbb{Z}|