-
Un ensemble est un groupement d’éléments ayant une certaine caractéristique en commun.
-
Un élément est un objet faisant partie d’un ensemble.
Il existe plusieurs types d’ensembles selon le nombre d’éléments qu’ils contiennent ou selon les caractéristiques de leurs éléments.
Un ensemble vide est un ensemble qui ne contient aucun élément. On le représente par le symbole |\varnothing| ou par 2 accolades vides : |\{\ \}.|
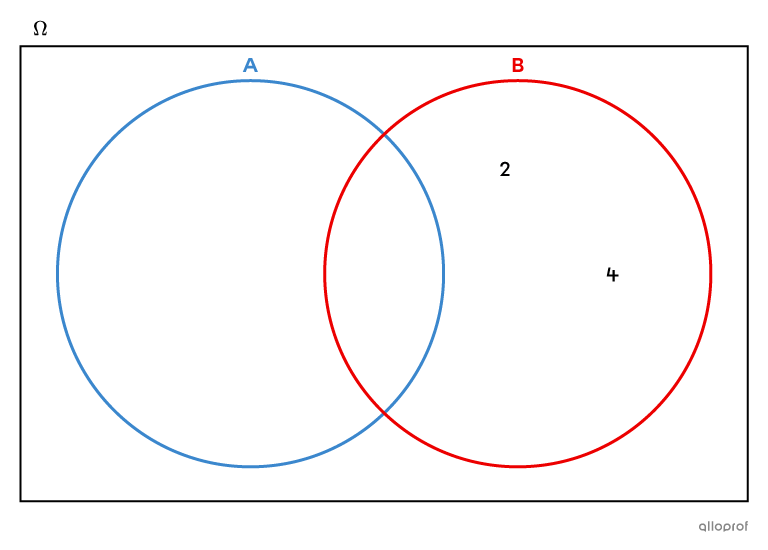
Dans ce diagramme de Venn, l'ensemble |A| est un ensemble vide, puisqu'il ne contient aucun élément.||A = \varnothing||
-
Un ensemble fini est un ensemble qui possède un nombre d'éléments déterminé. Ce nombre d'éléments est un nombre naturel.
-
Un ensemble infini est un ensemble qui possède un nombre d’éléments indéterminé. Cela signifie qu'il contient une infinité d'éléments.
Il est parfois question du cardinal ou de la cardinalité d'un ensemble. Il s’agit du nombre d'éléments contenus dans cet ensemble.
Les différents ensembles de nombres |(\mathbb N, \mathbb Z, \mathbb Q, \mathbb Q', \mathbb R)| sont des ensembles infinis.
Un singleton est un ensemble qui ne contient qu’un seul élément.
-
|A = \{2,4,6,8,10\}| est un ensemble fini qui contient |5| éléments.
-
|B = \{1,2,3, \ldots ,100\}| est un ensemble fini qui contient |100| éléments.
-
|C = \{\text{Les nombres premiers inférieurs à}\ 250\}| est un ensemble fini.
-
|D = \{\text{Les diviseurs de}\ 27\}| est un ensemble fini.
-
|E = \left\{\text{Les fractions équivalentes à}\ \dfrac{3}{4} \right\}| est un ensemble infini.
-
|F = \{\text{Les multiples de}\ 5\}| est un ensemble infini.
-
|G = \{12\}| est un singleton, car il s’agit d’un ensemble fini qui contient un seul élément.
Un ensemble-solution est un ensemble qui contient les différentes solutions d'une équation ou d’une inéquation donnée. Il peut contenir 0, une ou plusieurs solutions, selon le problème.
-
L'ensemble-solution de l'équation |2x+5=25| est |A=\{10\}.|
-
L'ensemble-solution de l'équation |2a+3b=8| est |B=\{(4,0), (1,2), (-2,4), (-5,6), \ldots \}.|
-
L'ensemble-solution de l'inéquation |4x< 12| est |C=\{x \in\mathbb R\ \vert\ x<3\},| c’est-à-dire tous les |x| qui font partie de l’ensemble référentiel des nombres réels et qui sont strictement inférieurs à |3.|
Pour les inéquations, il existe plusieurs représentations d’un ensemble-solution : la notation en compréhension, l’utilisation d’une droite numérique et l’intervalle.
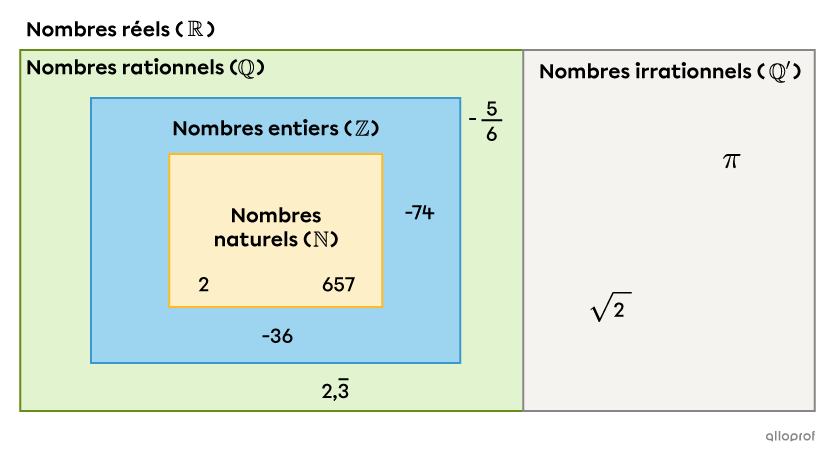
Un ensemble de nombres est un ensemble dont tous les éléments sont des nombres d’un certain type. Il en existe plusieurs :
-
les nombres naturels |\mathbb N,| comme |2| et |657;|
-
les nombres entiers |\mathbb Z,| comme |2,| |-74| et |-36;|
-
les nombres rationnels |\mathbb Q,| comme |2,| |-74,| |-\dfrac{5}{6}| et |2{,}\overline{3};|
-
les nombres irrationnels |\mathbb Q',| comme |\pi| et |\sqrt{2};|
-
les nombres réels |\mathbb R,| qui incluent tous les ensembles de nombres précédents.
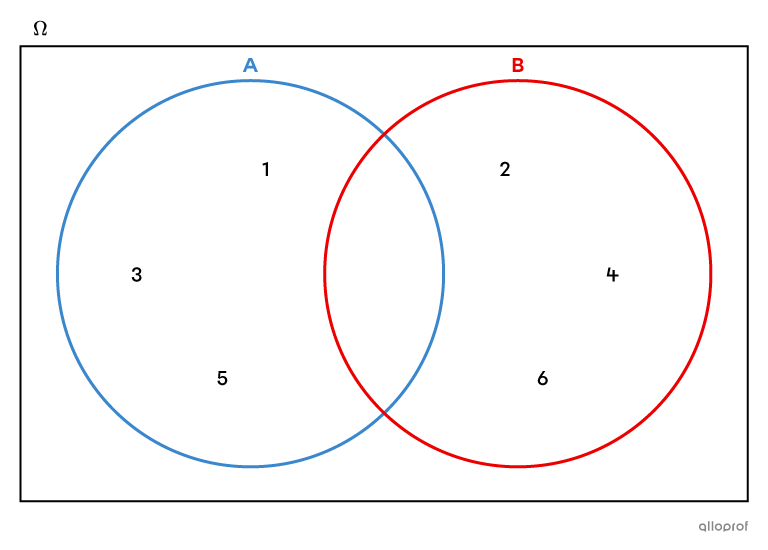
Des ensembles disjoints sont des ensembles qui n’ont aucun élément en commun.
L'intersection entre 2 ensembles disjoints est un ensemble vide et on peut écrire |A\cap B=\varnothing.|
Dans ce diagramme de Venn, l'ensemble |A| contient des nombres impairs, alors que l'ensemble |B| contient des nombres pairs. Ce sont 2 ensembles disjoints, puisque leur intersection est vide.
-
Des ensembles égaux sont des ensembles qui contiennent exactement les mêmes éléments.
-
Des ensembles qui ne sont pas égaux sont des ensembles différents.
Seule l'intersection entre des ensembles égaux contient des éléments. Ainsi, il ne peut pas y avoir un élément d'un ensemble qui ne fait pas aussi partie de l'autre ensemble.
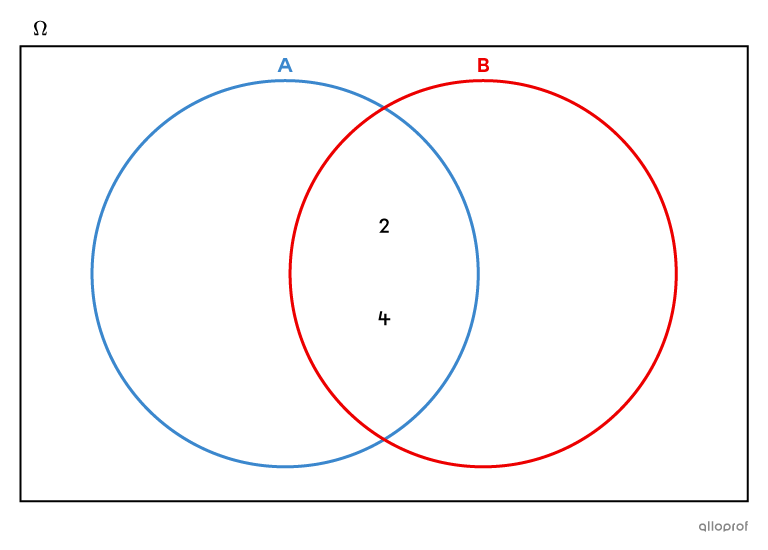
Dans ce diagramme de Venn, les ensembles |A = \{2, 4\}| et |B = \{2, 4\}| sont égaux, puisqu'ils contiennent exactement les mêmes éléments.
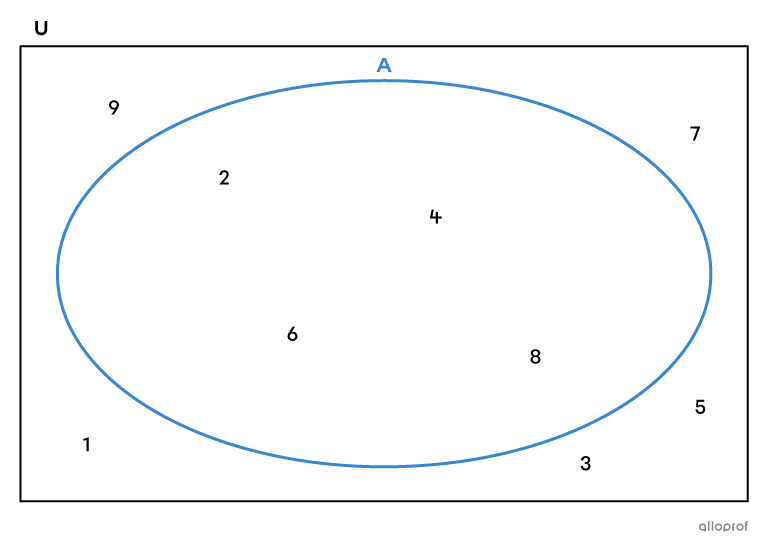
Dans le cadre d'une théorie ou d'un problème, l'ensemble référentiel |(U)| représente l'ensemble de tous les éléments considérés. Il s'agit en quelque sorte d'un ensemble de départ à partir duquel on peut définir d'autres ensembles.
Dans le cadre des fonctions, le domaine et le codomaine sont des ensembles référentiels. Dans le cadre des probabilités, l’univers des possibles |(\Omega)| est un ensemble référentiel.
L'ensemble |A = \{2, 4, 6, 8\}| regroupe les nombres pairs présents dans l'ensemble référentiel |U = \{1, 2, 3, 4, 5, 6, 7, 8, 9\}.|