Lorsqu’on classe les éléments de l’univers des possibles dans un diagramme de Venn, on s’intéresse souvent à l’intersection |(\cap)| ou à l’union |(\cup)| des ensembles. Cela amène à calculer des probabilités.
Dans l'animation interactive suivante, tu peux voir un diagramme de Venn à 2 ensembles (A et B). Tu peux cocher la case permettant de voir un 3e ensemble (C) si tu le souhaites. Par la suite, tu peux observer les intersections des différents ensembles, qui apparaitront hachurés, ou observer les différentes unions possibles.
L’intersection d’ensembles, notée à l’aide du symbole |\cap,| comprend les éléments communs à tous les ensembles étudiés. Elle est associée à la notion du « et » en probabilités.
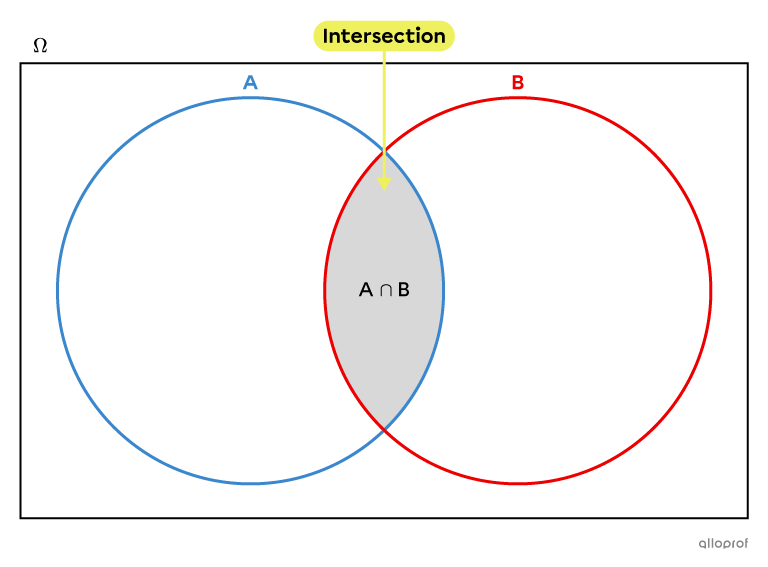
Dans un diagramme de Venn, l’intersection des ensembles |A| et |B,| notée |A \cap B,| est la zone située au centre du diagramme dont les éléments font partie à la fois de l’ensemble |A| et de l’ensemble |B.|
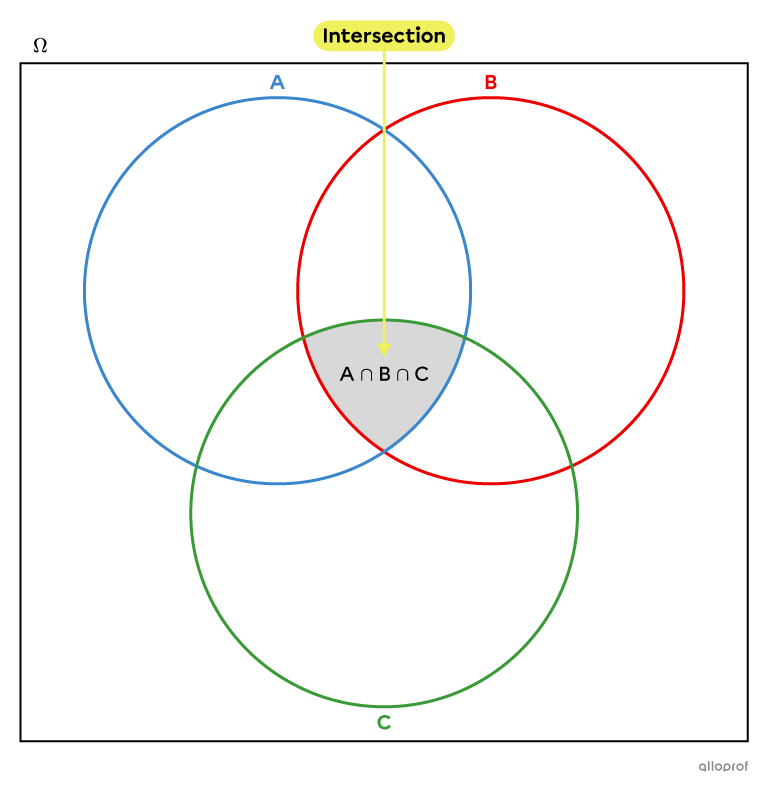
Dans un diagramme de Venn à 3 ensembles, l’intersection des ensembles |A,| |B| et |C,| notée |A\cap B\cap C,| est la zone située au centre du diagramme dont les éléments font partie à la fois de l’ensemble |A,| de l’ensemble |B| et de l’ensemble |C.|
Soit les 2 ensembles suivants.
|A :| Les nombres impairs inférieurs à |10|
|B :| Les multiples de |3| inférieurs à |10|
Voici la liste des éléments de chacun de ces ensembles.
|A= \{1, \color{#3a9a38}{3}, 5, 7, \color{#3a9a38}{9} \}|
|B = \{\color{#3a9a38}{3}, 6, \color{#3a9a38}{9} \}|
Les nombres |\color{#3a9a38}{3}| et |\color{#3a9a38}{9}| sont communs aux 2 ensembles parce qu’ils sont à la fois des nombres impairs et des multiples de |3| inférieurs à |10.| L'intersection des ensembles |A| et |B| se note donc de la façon suivante. ||A \cap B = \{3, 9\}||En représentant les ensembles |A| et |B| dans un diagramme de Venn où l’univers des possibles |(\Omega)| correspond à l’ensemble des nombres inférieurs à |10,| on remarque que les nombres |3| et |9| sont bel et bien situés dans la zone qui est commune aux ensembles |A| et |B.|

Soit les 3 ensembles suivants qui font partie de |\Omega=\{1, 2, 3, 4, 5, 6\}.|
|A :| Les nombres naturels inférieurs à |4|
|B :| Les nombres pairs
|C :| Les nombres compris entre |1| et |7|
Voici la liste des éléments de chacun de ces ensembles.
|A = \{1, \color{#3a9a38}{2}, 3 \}|
|B = \{ \color{#3a9a38}{2}, 4, 6 \}|
|C = \{ \color{#3a9a38}{2}, 3, 4, 5, 6 \}|
On peut les représenter dans le diagramme de Venn suivant.
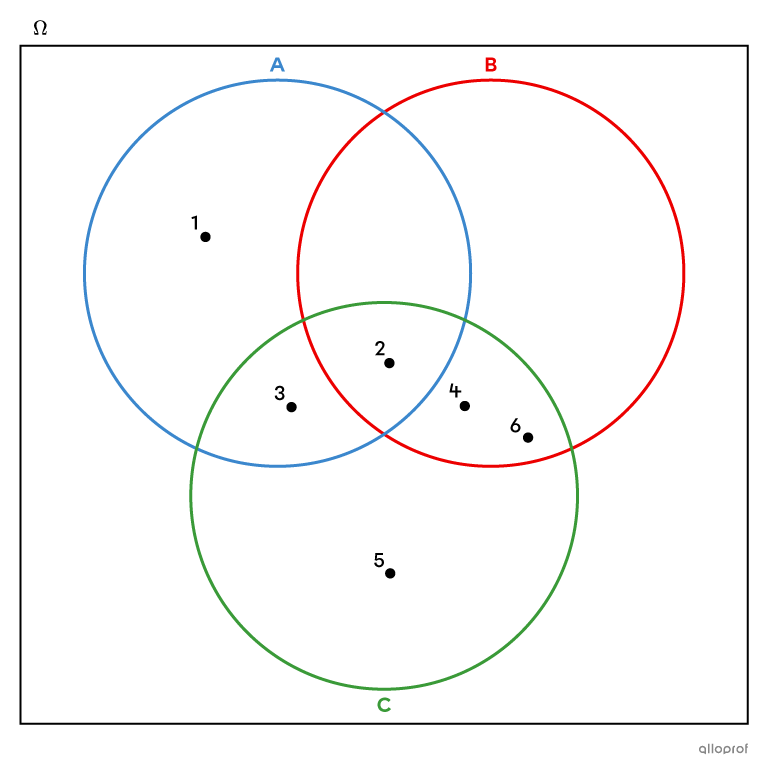
Le nombre |2| est le seul élément à être présent dans les 3 ensembles.||A \cap B \cap C = \{2\}||Il est possible de s’intéresser aux intersections des ensembles pris 2 à 2. On obtient alors les intersections suivantes.||\begin{align}A \cap B &= \{2\}\\ A\cap C &= \{2, 3\}\\B\cap C &= \{2, 4, 6\} \end{align}||
Remarque : Il est tout à fait possible que l’intersection de 2 ensembles soit identique à celle de 3 ensembles, comme c’est le cas dans cet exemple : |A \cap B \cap C=A \cap B.|
Il est possible que des ensembles n’aient aucun élément en commun. Dans ce cas, leur intersection est en fait un ensemble vide et on dit que les ensembles sont incompatibles.
Soit les 2 ensembles suivants.
|G = \{1,2,3,4,5\}|
|H = \{6,7,8\}|
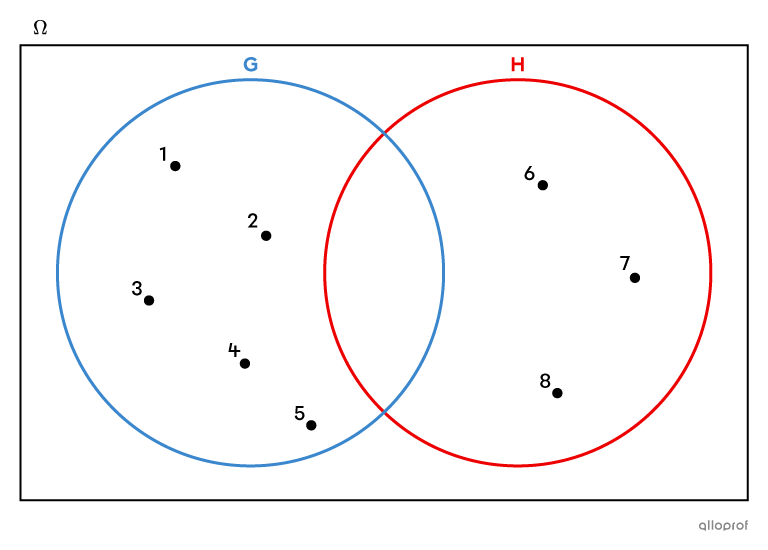
Aucun nombre n’est commun aux ensembles |G| et |H.| Leur intersection est un ensemble vide.||G \cap H = \{\ \}\ \text{ou}\ \varnothing||Les ensembles |G| et |H| sont donc incompatibles.
L'intersection |(\cap)| de 2 ensembles |A| et |B| s'exprime de la façon suivante. ||A \cap B = \lbrace x \in \Omega \mid x \in A \text{ et } x \in B \rbrace||
où
|\Omega :| univers des possibles
L'union (parfois nommée réunion) de 2 ensembles, notée à l’aide du symbole |\cup,| est l'ensemble qui contient tous les éléments appartenant à chaque ensemble ou aux 2 à la fois. L’union est donc associée à la notion du « ou » en probabilités.
Dans un diagramme de Venn, l’union des ensembles |A| et |B,| notée |A \cup B,| comprend tout ce qui se trouve à l’intérieur de l’ensemble |A| et de l’ensemble |B,| incluant la partie commune aux 2 ensembles.
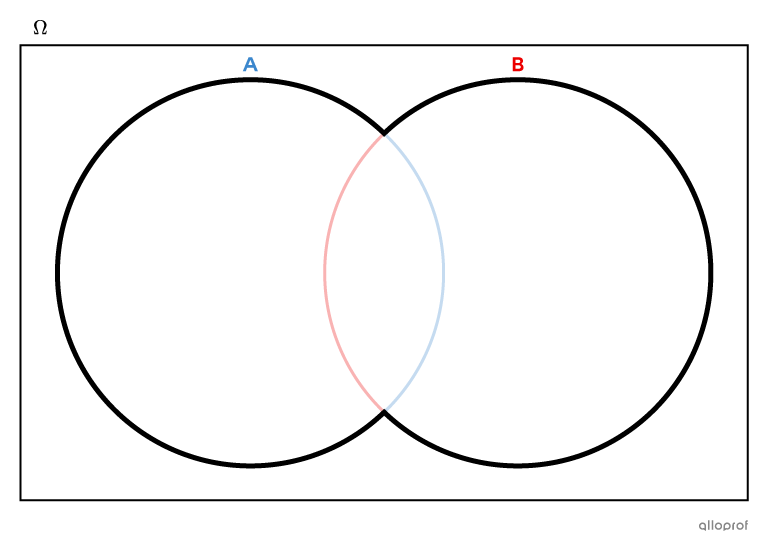
Dans un diagramme de Venn à 3 ensembles, l’union des ensembles |A,| |B| et |C,| notée |A\cup B\cup C,| comprend tout ce qui est situé à l’intérieur des 3 courbes.
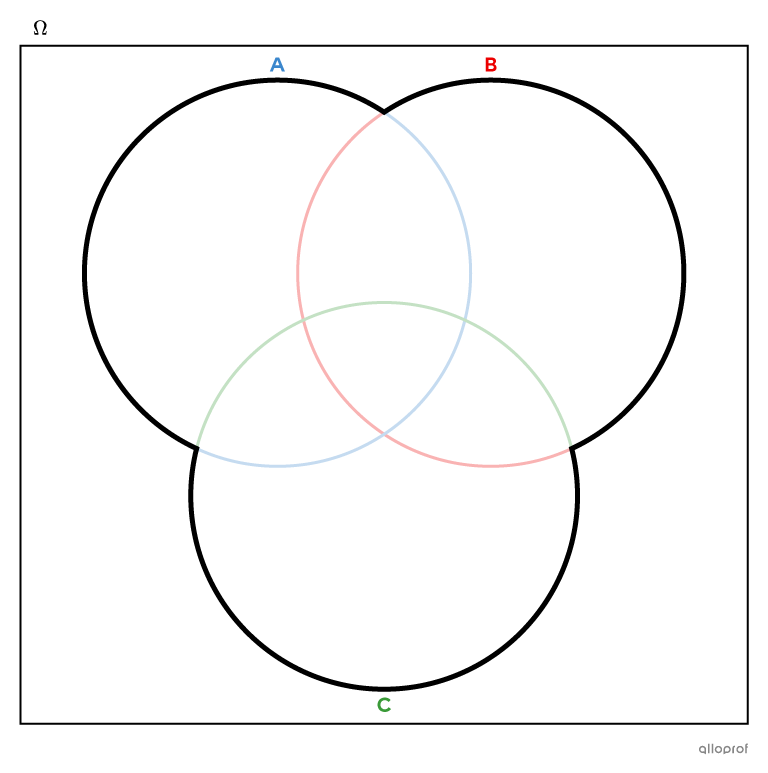
Pour trouver tous les éléments de l’union de |A| et |B| ou pour faire le dénombrement des ensembles |A| et |B,| on emploie la formule suivante.
Éléments de |A\cup B =| Éléments de |A\, +| Éléments de |B\, -| Éléments de leur intersection ||A\cup B = A + B - (A\cap B)||
Il est possible d’utiliser une formule similaire pour calculer la probabilité de choisir un nombre au hasard dans l’intersection de 2 ensembles.
||P(A\cup B) = P(A) + P(B) - P(A\cap B)||
Soit les nombres naturels inférieurs à |10| inclus dans les ensembles |A| et |B| suivants.
|A :| Les diviseurs de |12|
|B :| Les multiples de |3|
a) Quels sont les éléments qui font partie de l’union des ensembles |A| et |B|?
b) Combien y a-t-il d’éléments dans l’union de ces ensembles?
c) Quelle est la probabilité qu’un nombre naturel inférieur à |10| choisi au hasard fasse partie de l’union de ces ensembles?
-
Faire la liste des éléments de chaque ensemble||\begin{align}A &= \{1,2,3,4,6\} \\ B &= \{3, 6, 9\}\end{align}||
-
Remplir le diagramme de Venn
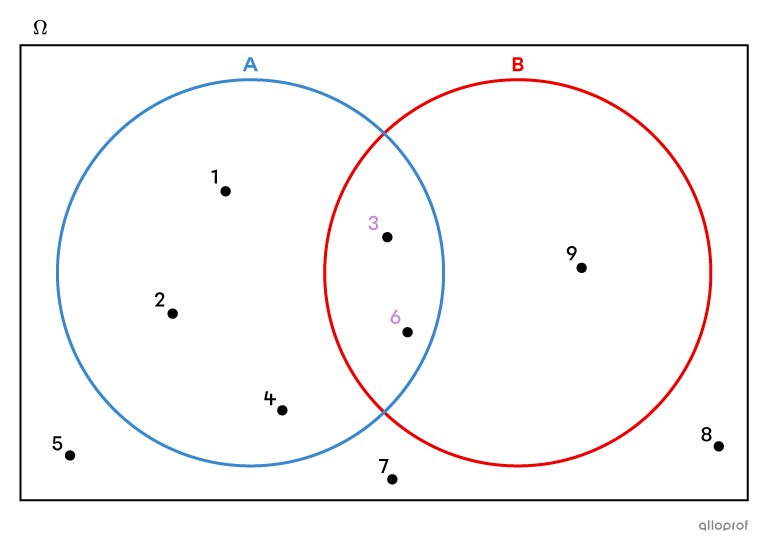
-
Déterminer l’intersection des 2 ensembles
L'intersection entre |A| et |B| est la suivante. ||A \cap B = \{ \color{#c58ae1}{3}, \color{#c58ae1}{6}\}|| -
Déterminer l'union des 2 ensembles en appliquant la formule appropriée
a) Pour déterminer les éléments qui sont dans l’union des 2 ensembles, on fait la démarche suivante. ||\begin{align}A \cup B &=\color{#3b87cd}A\quad+\quad \color{#ec0000}B\quad-\quad\color{#c58ae1}{(A\cap B)}\\ &= \{1, 2, \color{#c58ae1}3, 4, \color{#c58ae1}6 \} + \{\color{#c58ae1}3, \color{#c58ae1}6, 9 \} - \{\color{#c58ae1}3, \color{#c58ae1}6\} \\ &= \{1, 2, 3, 4, 6, 9\} \end{align}||
b) Pour faire le dénombrement de l’union des 2 ensembles, on fait le calcul suivant.||\begin{align}A \cup B &=\color{#3b87cd}A+ \color{#ec0000}B-\color{#c58ae1}{A\cap B}\\ &=\, \color{#3b87cd}5\, + \,\color{#ec0000}3 -\, \color{#c58ae1}{2} \\ &=\, 6 \ \text{éléments}\end{align}||
c) Pour calculer la probabilité qu’un nombre naturel inférieur à |10| choisi au hasard soit un diviseur de |12| ou un multiple de |3,| on fait le calcul suivant. ||\begin{align}P(A\cup B) &=P(\color{#3b87cd}A)+P( \color{#ec0000}B)-P(\color{#c58ae1}{A\cap B})\\ &=\ \ \dfrac{\color{#3b87cd}5}{9}\quad +\ \ \dfrac{\color{#ec0000}3}{9}\quad -\ \ \dfrac{\color{#c58ae1}{2}}{9} \\ &=\ \ \dfrac{6}{9}\end{align}||
Lorsque l’intersection de 2 ensembles est vide et que l’union des 2 ensembles correspond à l’univers des possibles, on dit que ces ensembles sont complémentaires.
L'union |(\cup)| des ensembles |A| et |B| s'exprime de la façon suivante. ||A \cup B = \lbrace x \in \Omega \mid x \in A \text{ ou } x \in B \rbrace||
où
|\Omega :| univers des possibles
|
|
||
|---|---|---|
|
||A \cap B = B \cap A|| |
||A \cup B = B \cup A|| |
|
|
||(A \cap B)\cap C = A\cap (B \cap C)|| |
||(A \cup B)\cup C = A\cup (B \cup C)|| |
|
|
L’intersection est distributive sur l’union. ||A \cap(B \cup C) = (A \cap B) \cup (A \cap C)|| |
L’union est distributive sur l’intersection. ||A \cup (B \cap C) = (A \cup B) \cap (A \cup C)|| |